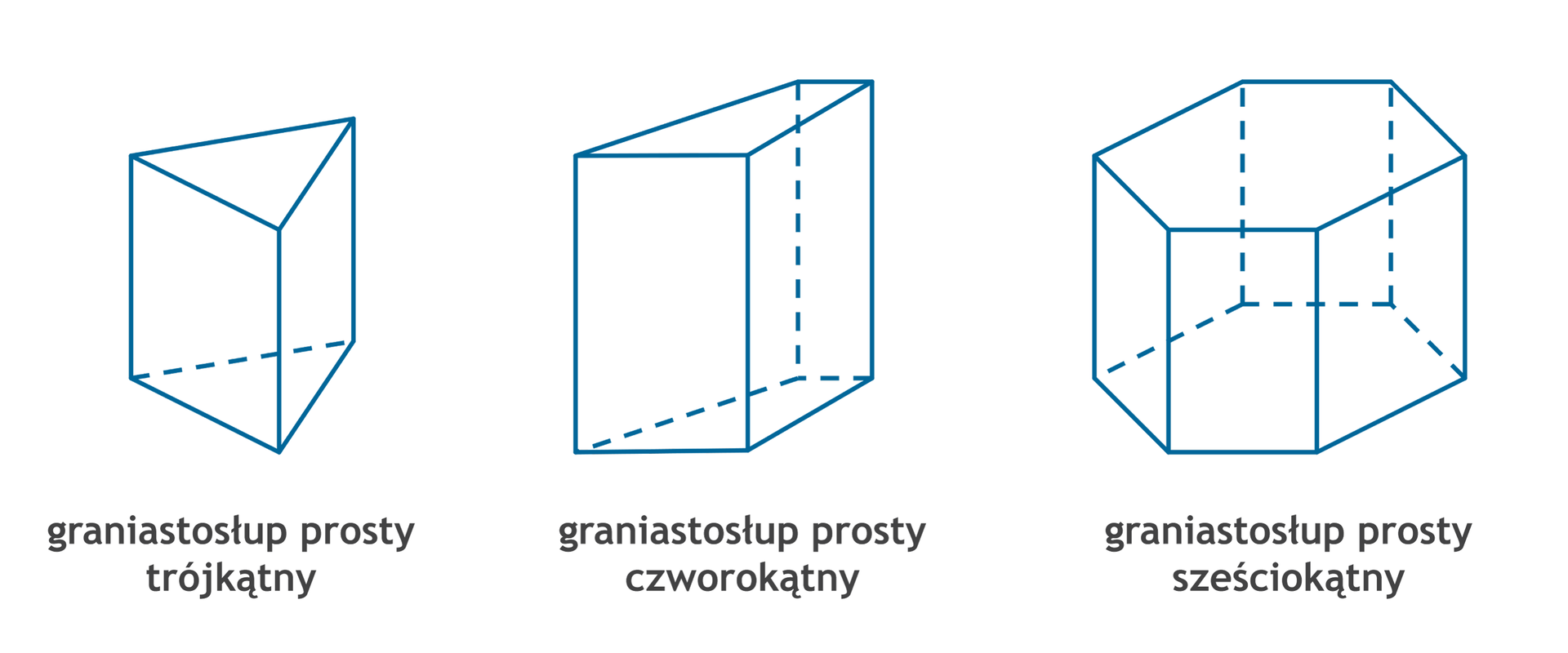
Rodzaje graniastosłupów

RvbLXqLqEKAQT1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Prostopadłościan i sześcian są przykładami graniastosłupów prostych.

Graniastosłup prosty ma dwie podstawy w kształcie przystających wielokątów, leżące w równoległych płaszczyznach. Ściany boczne są prostokątami prostopadłymi do podstaw.
Nazwa graniastosłupa zależy od wielokąta, będącego jego podstawą.

Graniastosłup prosty

Definicja: Graniastosłup prosty

Graniastosłup prosty to taka figura przestrzenna, która ma

dwie podstawy będące jednakowymi wielokątami,
ściany boczne będące prostokątami.

Nazwa graniastosłupa zależy od rodzaju wielokąta w podstawie.

RtrXmdhOuXMsr1

Rysunek graniastosłupa prostego trójkątnego, graniastosłupa prostego czworokątnego i graniastosłupa prostego sześciokątnego. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1LVqU6nxvdSW1

Jeśli podstawą graniastosłupa prostego jest wielokąt foremny (np. trójkąt równoboczny, kwadrat, pięciokąt foremny, sześciokąt foremny), wówczas graniastosłup taki nazywamy prawidłowym.

Inny rodzaj graniastosłupów to graniastosłupy pochyłe. Ich ściany boczne są równoległobokami. Najczęściej leżą w płaszczyznach, które nie są prostopadłe do podstaw.

Elementy graniastosłupa

Ważne!

Graniastosłup ma dwie podstawy w kształcie wielokątów. Liczba ścian bocznych zależy od liczby boków podstawy. Ściany boczne są prostokątami (w przypadku graniastosłupów prostych) lub równoległobokami. Krawędzie boczne są równoległe i równe.

Obejrzyj dokładnie model graniastosłupa.

R1XtD0zSn2x2O1

Rysunek graniastosłupa z zaznaczonymi: podstawą górną, podstawą dolną, wierzchołkiem, ścianą boczną, krawędzią podstawy i krawędzią boczną. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RRQ4c2iSsOeok1

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DiN0qGQJP

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY NC 3.0.

Przykład 1

Rysunek przedstawia graniastosłup.

Określ liczbę wierzchołków podstawy dolnej i liczbę wszystkich wierzchołków.
Ile krawędzi bocznych ma ten graniastosłup? Ile ma wszystkich krawędzi?
Ile ścian bocznych ma graniastosłup? Ile ma wszystkich ścian?
R1LEA7uE0KjO71
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przykład 2

Podstawą graniastosłupa prawidłowego jest trójkąt o polu $25 \sqrt{3} c m^{2}$ . Wysokość graniastosłupa jest równa $12 cm$ . Oblicz, ile centymetrów listewek potrzeba na wykonanie szkieletowego modelu tego graniastosłupa.

R11K1PgVK1sTh1

Rysunek graniastosłupa prostego trójkątnego. Wszystkie krawędzie podstawy są równe a, wysokość bryły H. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Graniastosłup jest prawidłowy trójkątny, zatem jego podstawą jest trójkąt równoboczny.
Obliczamy długość a krawędzi podstawy – korzystamy ze wzoru na pole trójkąta równobocznego.

\frac{\sqrt{3}}{4} a^{2} = P \frac{\sqrt{3}}{4} a^{2} = 25 \sqrt{3} a^{2} = 100

a = \sqrt 100 a = 10 cm

Wszystkie krawędzie boczne graniastosłupa są równe i mają długość $12 cm$ .
Graniastosłup ma $6$ krawędzi podstaw i $3$ krawędzie boczne. Zatem potrzeba $6$ listewek długości $10 cm$ i trzech długości $12 cm$ .

6 \cdot 10 + 3 \cdot 12 = 60 + 36 = 96

Odpowiedź.
Na wykonanie modelu graniastosłupa potrzeba $96 cm$ listewek.
Wysokością graniastosłupa nazywamy odległość między płaszczyznami zawierającymi jego podstawy. W przypadku graniastosłupów prostych, wysokość jest równa długości krawędzi bocznej.

RBZaWARuCeRfd1

Rysunek dwóch graniastosłupów o wysokości równej H. Pierwszy graniastosłup pochyły o podstawie kwadratu. Drugi graniastosłup prosty o podstawie sześciokąta. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przekątna graniastosłupa to odcinek łączący dwa wierzchołki leżące w różnych podstawach i różnych ścianach bocznych.

R182WlLIPfwj31

Rysunek graniastosłupa prostego czworokątnego z poprowadzonymi przekątnymi graniastosłupa d i e. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

igLvS3hLwi_d5e253

Rysowanie graniastosłupów

Rysowanie graniastosłupa najlepiej rozpocząć od narysowania jego podstawy dolnej. Następnie rysujemy krawędzie boczne i łączymy ich końce, tworząc wielokąt będący podstawą górną. Niewidoczne krawędzie warto zaznaczyć liniami przerywanymi.

Przykład 3

Narysuj graniastosłup prosty, który w podstawie ma pięciokąt.

RXUaJyVALmbaY1

classicmobile

Ćwiczenie 1

Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

R1KY8nUspAjRU

Podstawą graniastosłupa prawidłowego trójkątnego jest trójkąt prostokątny.
Podstawy graniastosłupa są wzajemnie prostopadłe.
Graniastosłup ma tyle krawędzi bocznych, ile ma wierzchołków.
Każda z podstaw graniastosłupa pochyłego ma inną liczbę krawędzi.

static

Ćwiczenie 2

Uzupełnij tabelę, Określ w każdym z graniastosłupów liczbę ścian bocznych, wierzchołków, krawędzi bocznych i podstaw.

RuFRP6tw81lbz1

Rysunek czterech graniastosłupów: A - graniastosłup o podstawie czworokąta, B - graniastosłup o podstawie trójkąta, C -graniastosłup o podstawie kwadratu, D - graniastosłup o podstawie czworokąta. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Uzupełnij tabelkę.

Tabela. Dane
Nazwa graniastosłupa	Liczba ścian bocznych	Liczba wierzchołków	Liczba krawędzi bocznych	Liczba podstaw
$A$
$B$
$C$

Tabela. Dane
Nazwa graniastosłupa	Liczba ścian bocznych	Liczba wierzchołków	Liczba krawędzi bocznych	Liczba podstaw
$A$	$4$	$8$	$4$	$2$
$B$	$3$	$6$	$3$	$2$
$C$	$4$	$8$	$4$	$2$
$D$	$4$	$8$	$4$	$2$

classicmobile

Ćwiczenie 3

Wskaż figurę, która nie może być podstawą graniastosłupa.

R1YqpNaiqAv3L1

Rysunki czterech figur: siedmiokąta, trapezu, sześciokąta i elipsy. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1TAY9568Iey3

static

classicmobile

Ćwiczenie 4

Pewien graniastosłup ma $16$ wierzchołków. Ile krawędzi ma ten graniastosłup?

R1RzVeHnFTrq5

$32$
$64$
$8$
$24$

static

Ćwiczenie 4

Pewien graniastosłup ma $16$ wierzchołków. Ile krawędzi ma ten graniastosłup?

R17MMtQtRER88

$32$
$64$
$8$
$24$

Ćwiczenie 5

Uzupełnij zdania.

Graniastosłup, który nie ma przekątnej, ma ...krawędzi. Jego podstawą jest…
Sześcian to graniastosłup prawidłowy …
Podstawą graniastosłupa prawidłowego sześciokątnego jest….

$9$ , trójkąt
czworokątny
sześciokąt foremny

classicmobile

Ćwiczenie 6

Nie istnieje graniastosłup, który ma

RJsAWY9rkabCQ

$7$ wierzchołków
$7$ krawędzi bocznych
$7$ krawędzi jednej z podstaw
wysokość równą $7$

static

Ćwiczenie 6

Nie istnieje graniastosłup, który ma

R1cN7EVlQhhpO

$7$ wierzchołków
$7$ krawędzi bocznych
$7$ krawędzi jednej z podstaw
wysokość równą $7$

classicmobile

Ćwiczenie 7

Prawdą jest, że

R1KTL2Z10MyHy

W graniastosłupie prawidłowym wszystkie krawędzie są równe.
Jeśli wszystkie krawędzie graniastosłupa są równe, to jest to graniastosłup prawidłowy.
Liczba wszystkich krawędzi graniastosłupa prawidłowego jest zawsze parzysta.
Krawędzie boczne graniastosłupa prostego są równe.

static

classicmobile

Ćwiczenie 8

Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

RDhM4vqd8CSMP

Każdy prostopadłościan jest graniastosłupem prostym.
Każdy graniastosłup prawidłowy czworokątny jest sześcianem.
Każdy sześcian jest graniastosłupem prawidłowym czworokątnym.

static

igLvS3hLwi_d5e618

classicmobile

Ćwiczenie 9

Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

R1IDZ05DTEbUX

Jeśli w graniastosłupie prostym wszystkie ściany są przystającymi kwadratami, to graniastosłup ten jest prawidłowy.
Jeśli w graniastosłupie prostym podstawy są wielokątami przystającymi, to graniastosłup ten jest prawidłowy.
Jeśli w graniastosłupie prostym ściany boczne są przystającymi prostokątami, to graniastosłup ten jest prawidłowy.

static

classicmobile

Ćwiczenie 10

Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

RJpOnqc88RTS1

W graniastosłupie prostym ściany boczne są prostokątami.
W graniastosłupie krawędzie boczne są prostopadłe do podstaw.
Graniastosłup prawidłowy jest graniastosłupem prostym.
W graniastosłupie prawidłowym podstawy są wielokątami foremnymi.
W graniastosłupie prawidłowym ściany boczne są przystającymi prostokątami

static

R2LhxdsrcqaLn1

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DiN0qGQJP

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY NC 3.0.

classicmobile

Ćwiczenie 11

Zaznaczony odcinek w graniastosłupie to:

R1J5Bqr3gOB6w1

Rysunek graniastosłupa o podstawie pięciokąta wklęsłego. Zaznaczono odcinek, który łączy dwa wierzchołki należące do różnych podstaw i różnych ścian bocznych. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ru7eleVr4Kx0N

przekątna ściany bocznej
wysokość
przekątna podstawy
przekątna graniastosłupa

static

Ćwiczenie 12

R1b0WUkCDmadh1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 13

Podaj, ile krawędzi, ścian i wierzchołków ma graniastosłup, którego podstawa jest:

ośmiokątem
dwudziestokątem
stukątem

$24$ krawędzie, $8$ ścian $+$ $2$ podstawy, $16$ wierzchołków
$60$ krawędzi, $20$ ścian $+$ $2$ podstawy, $40$ wierzchołków
$300$ krawędzi, $100$ ścian $+ 2$ podstawy, $200$ wierzchołków

Ćwiczenie 14

W miejsce kropek wpisz odpowiednią liczbę.

Liczba krawędzi graniastosłupa o $20$ wierzchołkach. -…
Liczba ścian bocznych graniastosłupa, mającego $15$ krawędzi.-…
Liczba wierzchołków graniastosłupa zbudowanego z $22$ ścian. -…

$30$
$5$
$40$

Ćwiczenie 15

W miejsce kropek wpisz odpowiednią liczbę.

Liczba przekątnych graniastosłupa o podstawie czworokątnej …
Liczba przekątnych graniastosłupa o podstawie pięciokątnej …
Liczba przekątnych graniastosłupa o podstawie sześciokątnej …
Liczba przekątnych graniastosłupa o podstawie siedmiokątnej …

Ćwiczenie 16

RVLm3fmd2UBiE1

Uzupełnij.

a) Graniastosłup o podstawie czworokątnej posiada ............ przekątne.
b) Graniastosłup o podstawie pięciokątnej posiada ............ przekątnych.
c) Graniastosłup o podstawie sześciokątnej posiada ............ przekątnych.
d) Graniastosłup o podstawie siedmiokątnej posiada ............ przekątnych.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 17

Ile przekątnych ma

graniastosłup ośmiokątny?
graniastosłup stukątny?
graniastosłup n‑kątny?

$40$
$(100 - 3) \cdot 100$
$(n - 3) \cdot n$

classicmobile

Ćwiczenie 18

Podstawą graniastosłupa prostego o wysokości $10 cm$ jest trójkąt prostokątny, którego przyprostokątne mają długości $2 cm$ i $3 cm$ . Najdłuższa z przekątnych ścian bocznych ma długość

RG2V5th29SDpU

$\sqrt 113 cm$
$10 cm$
$\sqrt 9 cm$
$\sqrt 13 cm$

static

Ćwiczenie 18

RA5BxnYPi0AY4

$\sqrt 113 cm$
$10 cm$
$\sqrt 9 cm$
$\sqrt 13 cm$

Ćwiczenie 19

Przekątna ściany bocznej graniastosłupa prawidłowego trójkątnego jest nachylona do podstawy pod kątem $60 °$ . Krawędź podstawy ma długość $2 cm$ . Oblicz długość tej przekątnej i wysokość graniastosłupa.

długość przekątnej - $4 cm$ , wysokość - $2 \sqrt{3} cm$

Ćwiczenie 20

W graniastosłupie prawidłowym, którego wysokość jest równa $10 cm$ , podstawą jest sześciokąt o krawędzi długości $2 cm$ . Oblicz długości przekątnych tego graniastosłupa.

$d_{1} = \sqrt{112} cm$ , $d_{2} = \sqrt{116} cm$

Ćwiczenie 21

Oblicz sumę długości krawędzi graniastosłupa prawidłowego o wysokości równej $4 dm$ , którego podstawą jest:

trójkąt o boku długości $9 cm$
kwadrat o boku długości $5 cm$
pięciokąt o boku długości $1 dm$

$174 cm$
$200 cm$
$300 cm$

Prostopadłościan

Pole powierzchni graniastosłupa

Graniastosłup - opis

Rodzaje graniastosłupów

Elementy graniastosłupa

Rysowanie graniastosłupów