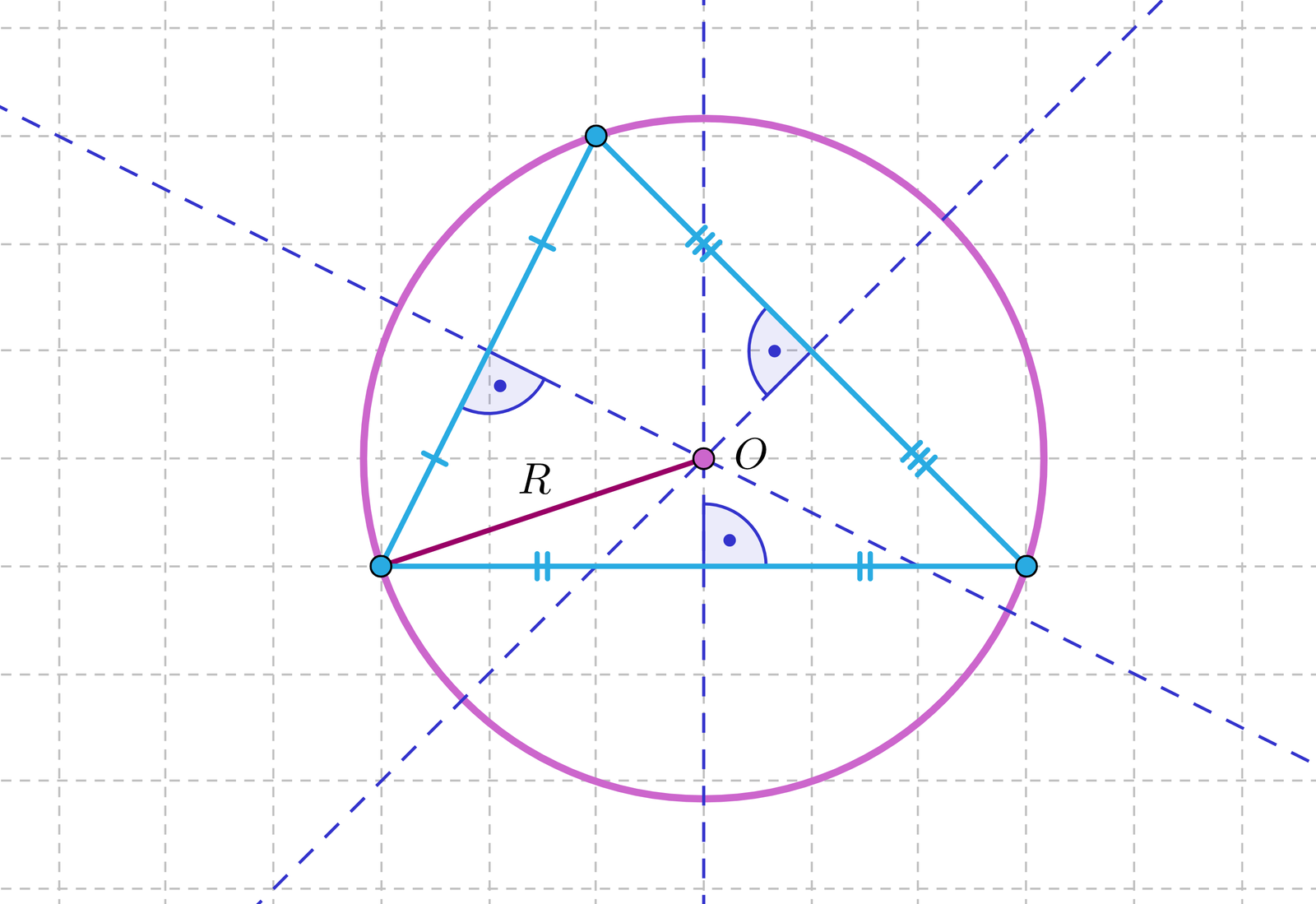
Aplet
Polecenie 1
Przeanalizuj działanie apletu. Za każdym razem określ położenie środka okręgu opisanego na trójkącie, w zależności od wybranego rodzaju trójkąta.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dn75LnvG4
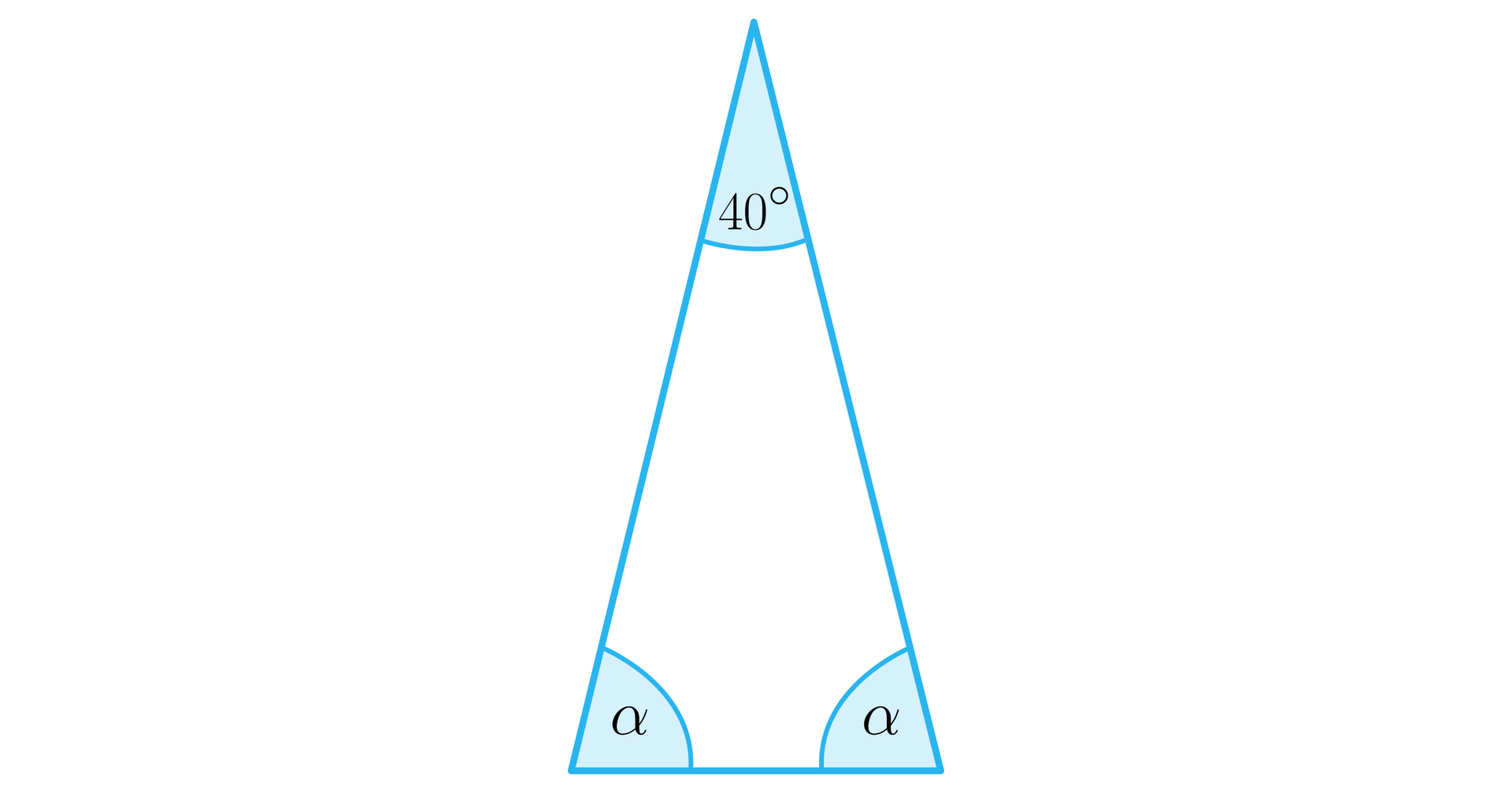
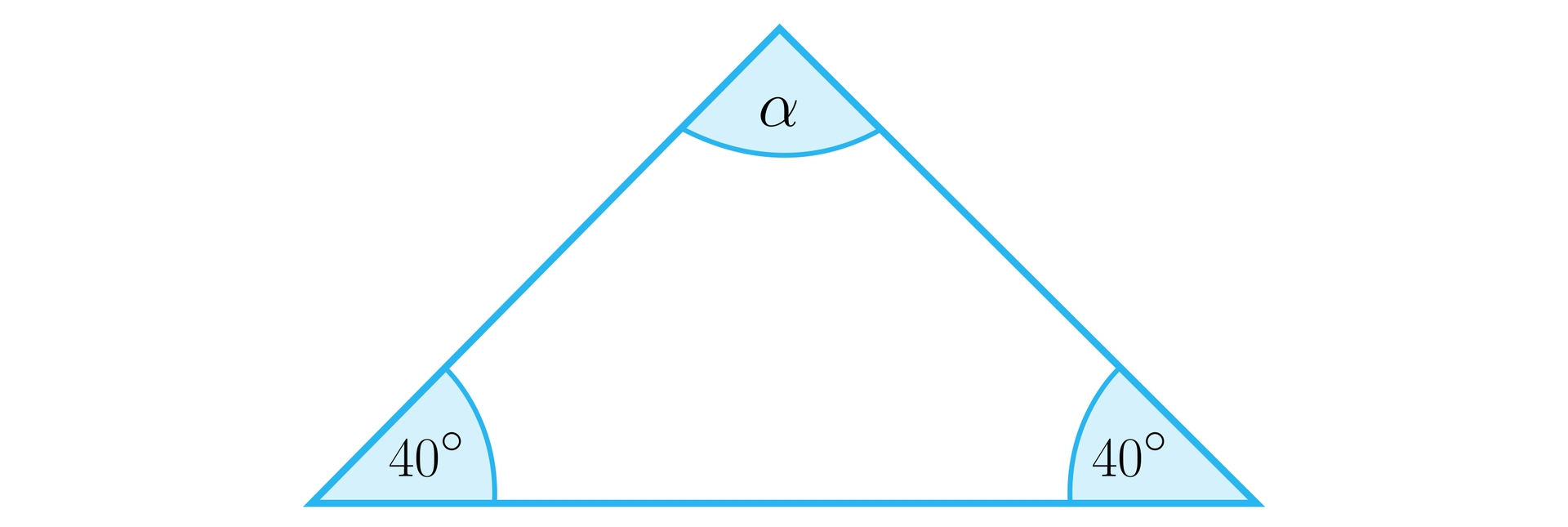
Polecenie 2
W trójkącie równoramiennym jeden z kątów ma miarę . Określ położenie środka okręgu opisanego na tym trójkącie.