Własności figur geometrycznych na płaszczyźnie
2. Kąty wierzchołkowe i przyległe
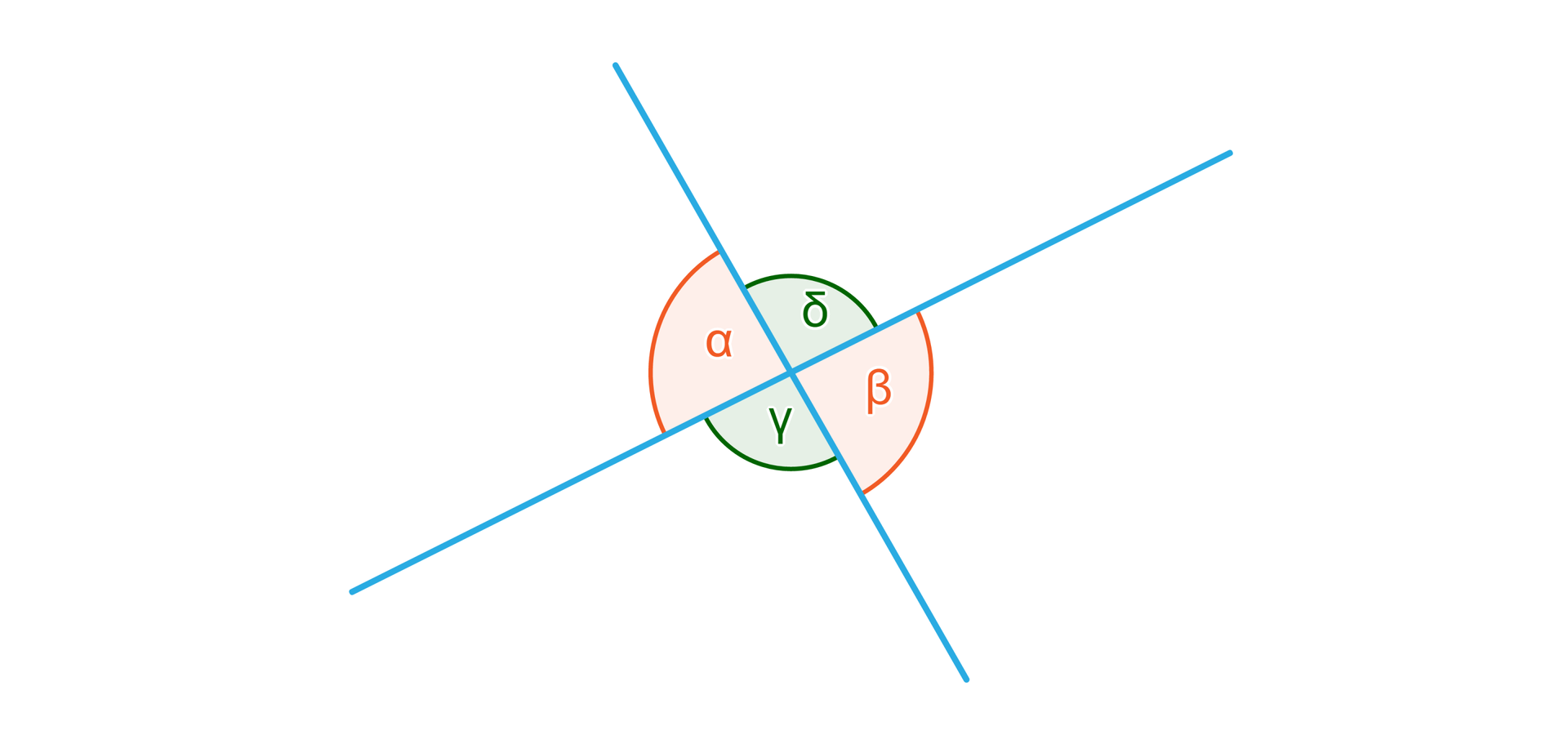
Dwie przecinające się proste wyznaczają cztery kąty. Wiele takich sytuacji możemy zauważyć w otaczajacym nas świecie.

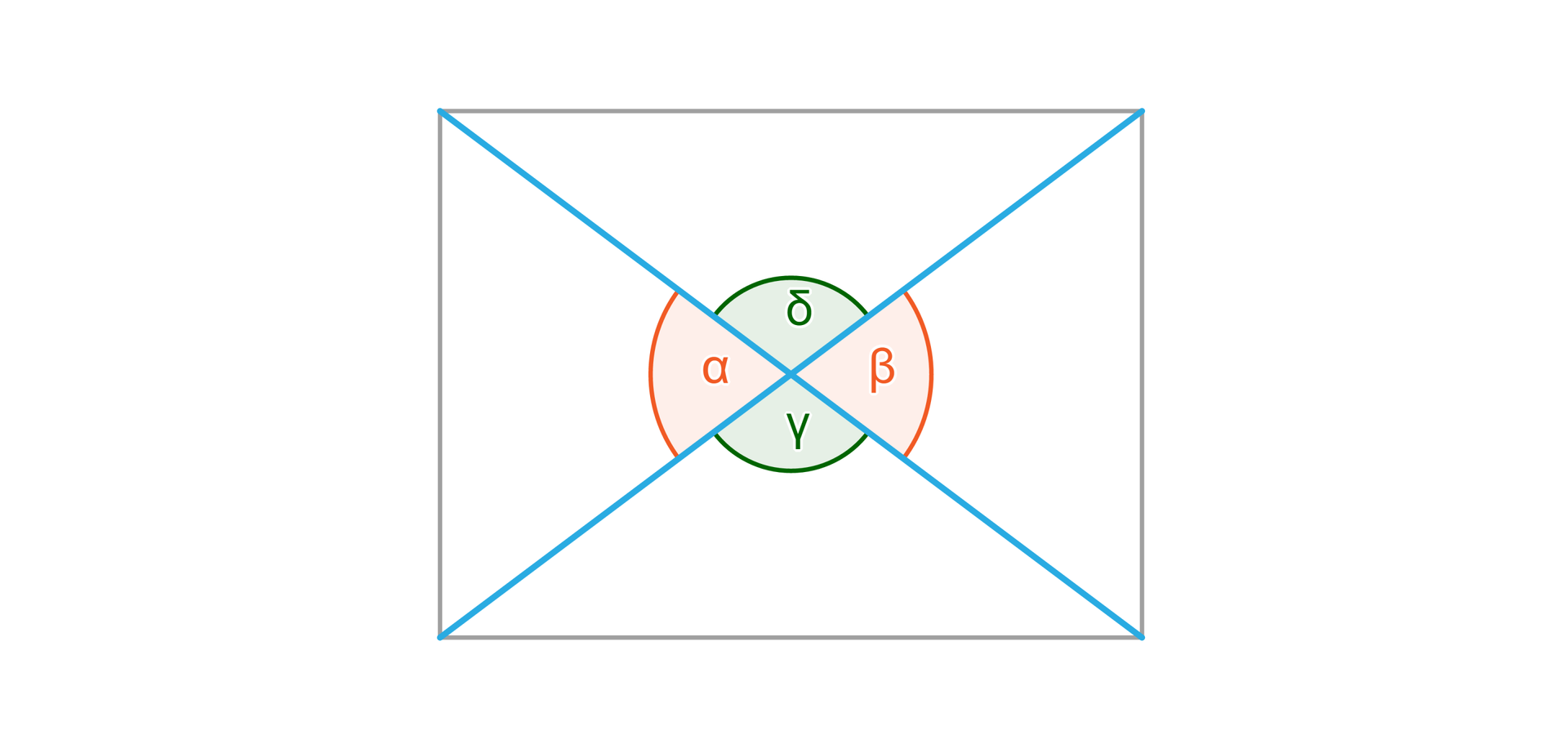
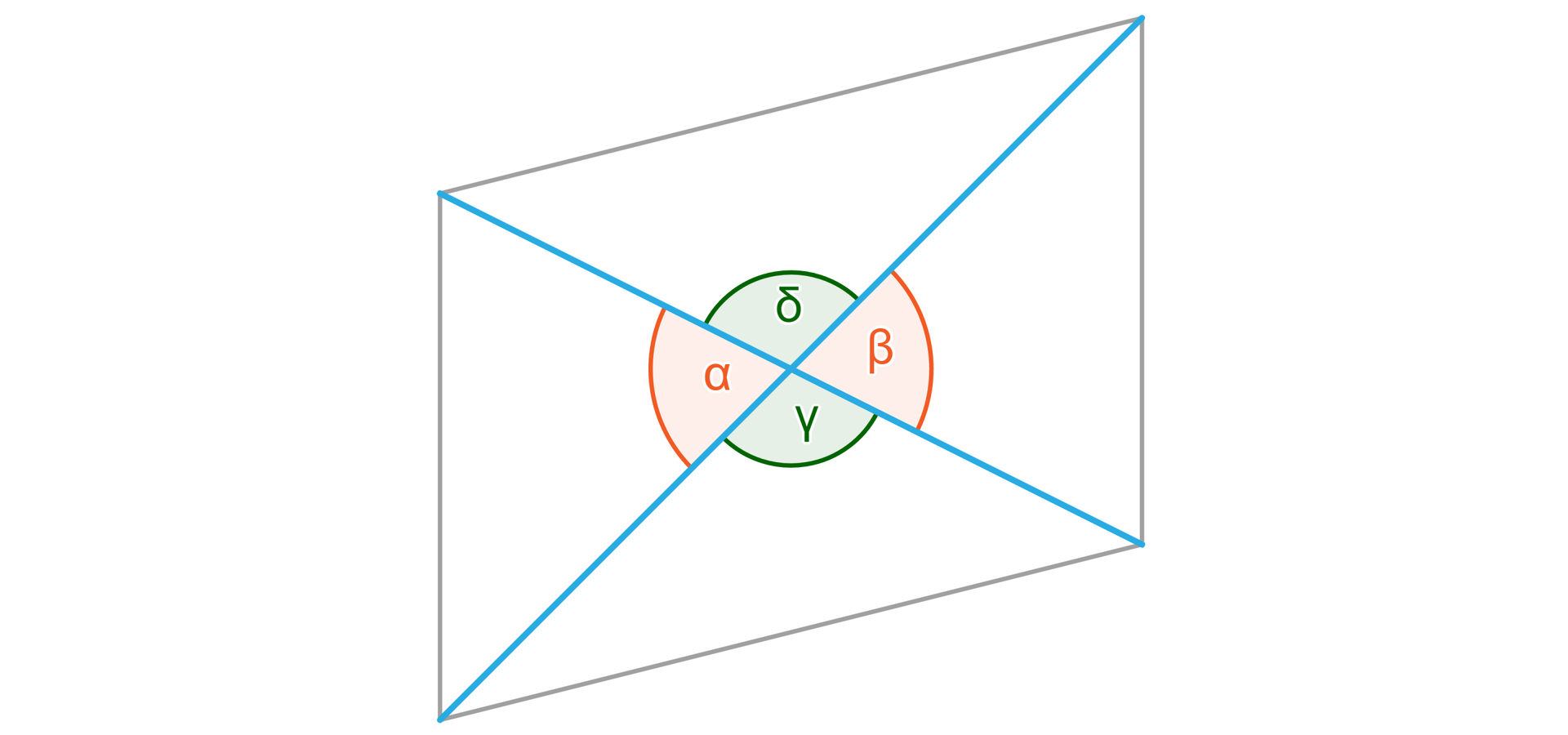
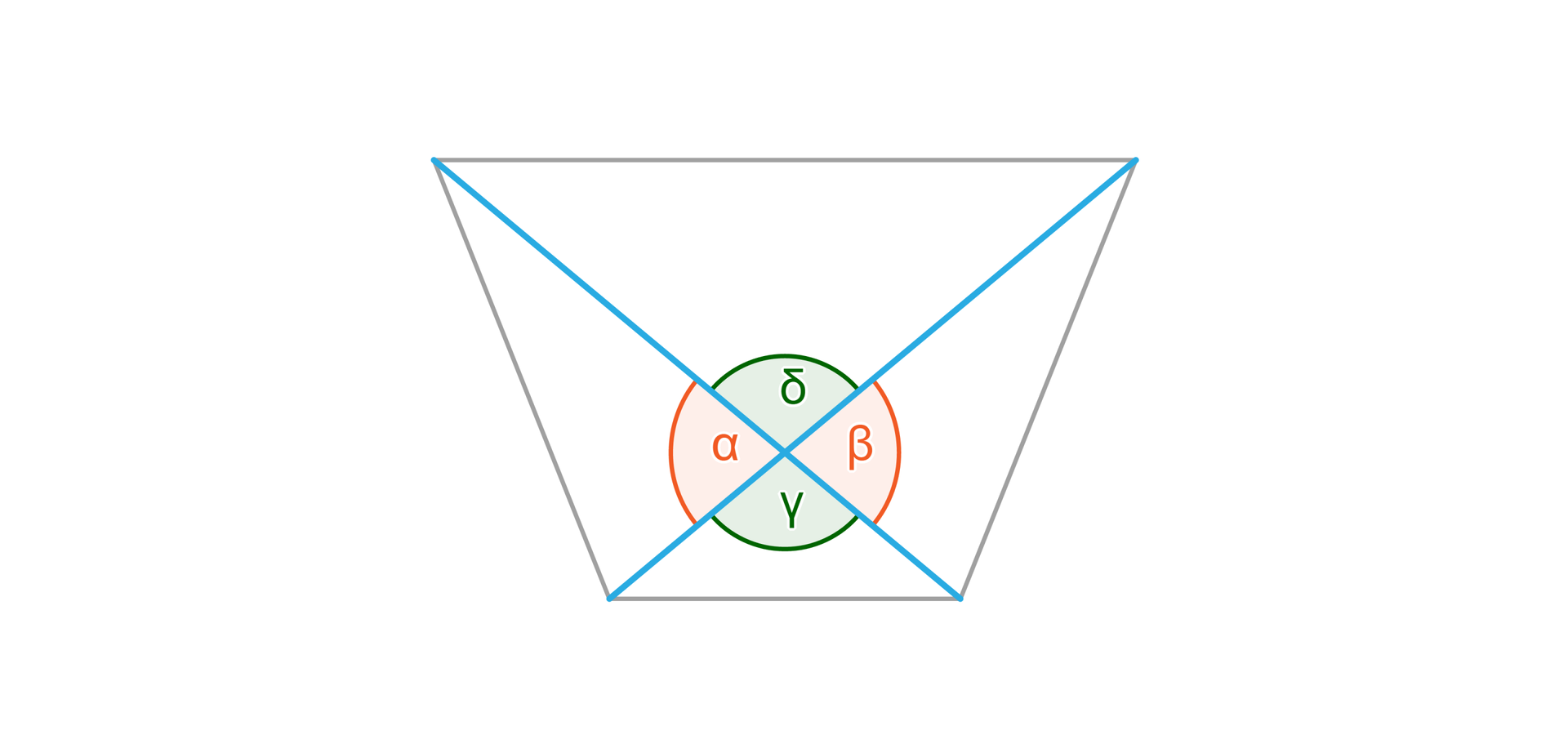
Podobnie przekątne w czworokącie wypukłym przecinają się i wyznaczają cztery kąty. Na poniższych rysunkach widać dwie przecinające się proste oraz przekątne w prostokącie, równoległoboku i trapezie.
W tym materiale poznasz zależności między tymi czterema kątami
Dwie półproste o wspólnym początku rozcinają płaszczyznę na dwie części. Każdą z tych części, wraz z tymi półprostymi nazywamy kątem.
Wierzchołkiem kąta nazywamy wspólny początek obu półprostych, a każdą z półprostych nazywamy ramieniem kąta.
Półproste i wyznaczają dwa kąty. Każdy z nich możemy oznaczyć symbolem . Aby wskazać o który kąt chodzi, zaznaczamy go odpowiednim łukiem.
Zapoznaj się z poniższą animacją, która opisuje konstrukcję i budowę kąta.

Film dostępny pod adresem /preview/resource/R1eL9Qx42gfYG
Co to jest kąt?
Rodzaje kątów
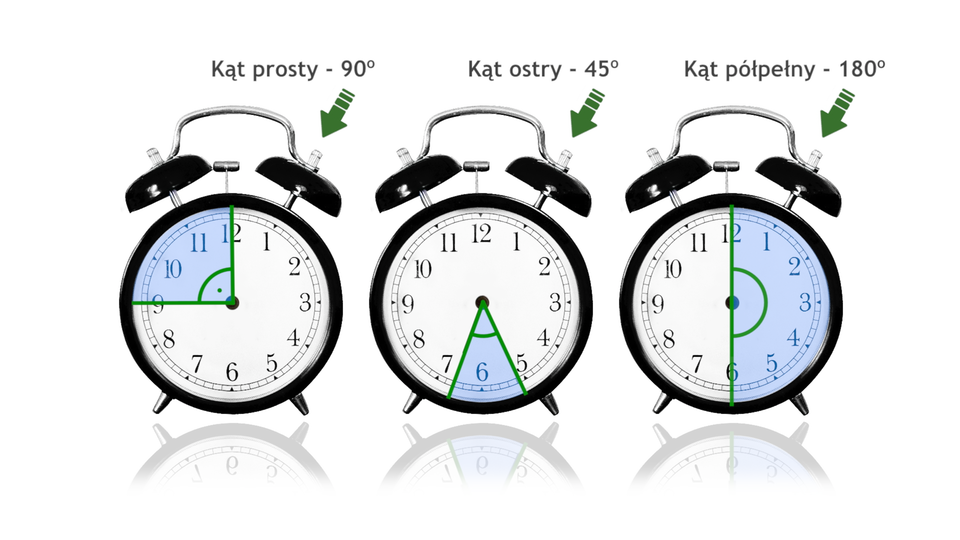
Film dostępny pod adresem /preview/resource/RPW9Gng89MtTs
Filmik pokazujący różne kąty za pomocą zegarów.
Jeśli ramiona kąta uzupełniają się do prostej, to taki kąt nazywamy półpełnym.
RUFhnMnsNPAkA1 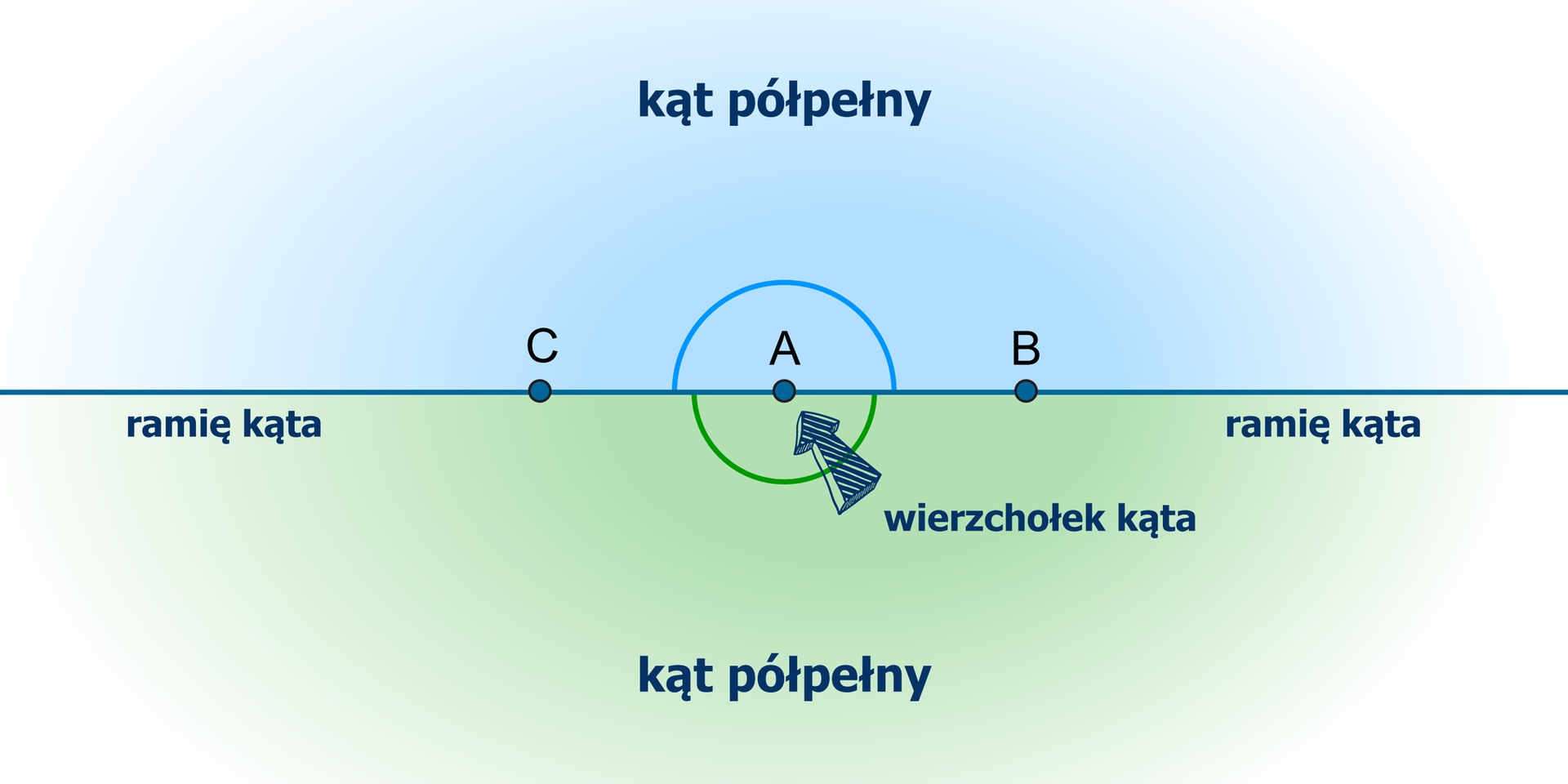 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Gdy ramiona kąta pokrywają się, wyznaczają kąt pełny lub kąt zerowy.
R1FbgaGlBjWeF1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Najczęściej używaną jednostką miary kąta jest stopień.
Jeden stopień to minut kątowych . Jedna minuta to sekund .
Kąty mające tę samą miarę nazywać będziemy kątami równymi lub przystającymi.
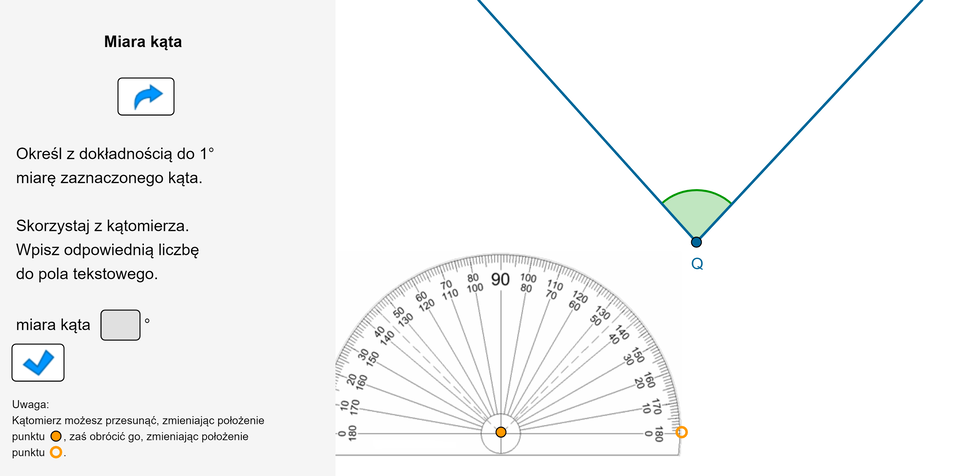
Uruchom aplet, aby wykonać polecenie w nim zawarte.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DqIN54whO
Jeśli ramiona kąta uzupełniają się do prostej, to taki kąt nazywamy 1. kątomierza, 2. półpełnym.
Przesuwając punkt , ustaw ramię kąta tak, aby miara tego kąta była równa podanej wartości. Skorzystaj z kątomierza.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DqIN54whO
Kąt, którego miara jest mniejsza od , ale większa od , nazywamy kątem ostrym.
Kąt, którego miara jest równa , nazywamy kątem prostym.
Kąt, którego miara jest większa od , ale mniejsza od , nazywamy kątem rozwartym.
RXXkRDlXtrjCC1 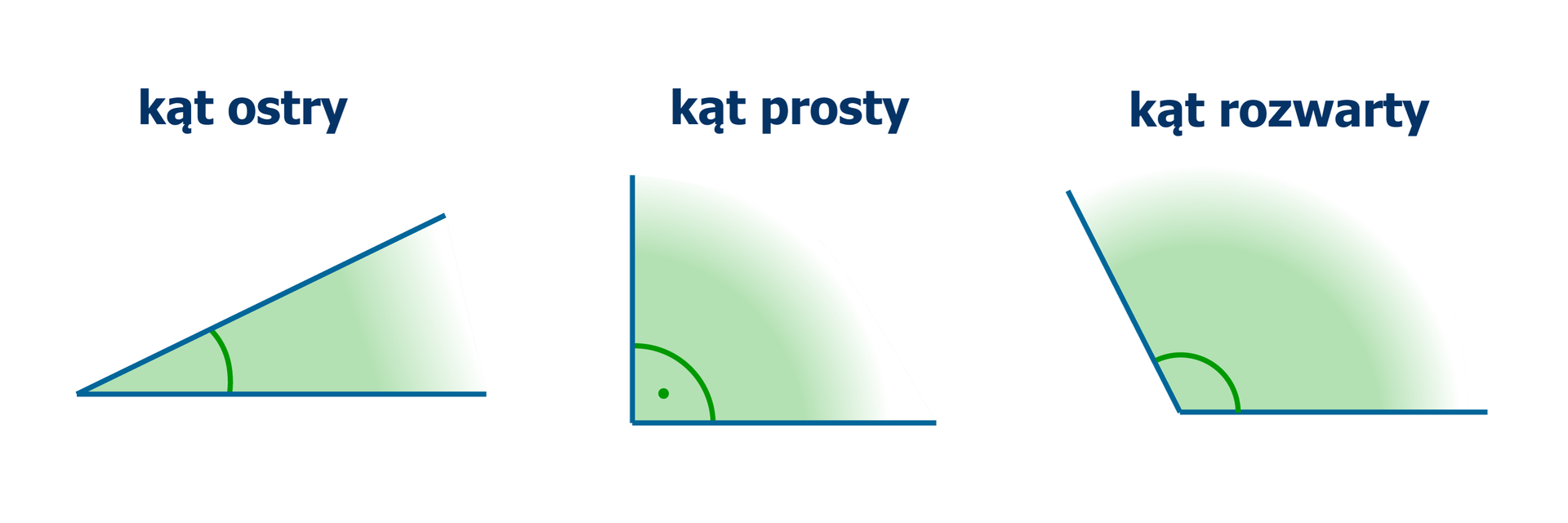 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Kąty, których miara jest mniejsza od lub równa nazywamy kątami wypukłymi.
Kąty, których miara jest większa od , ale mniejsza od , to kąty wklęsłe.
R1EO4gfhBPYa31  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
W naukach przyrodniczych najczęściej wykorzystywaną miarą kąta jest miara łukowa. Jednostką jest radian. Miary kątów pojawiają się w wielu wzorach fizycznych. Kąty wyrażone w radianach dają prostsze wyniki niż miary wyrażone w stopniach. Jednakże mierzenie kątów w stopniach w życiu codziennym jest tak popularne, że matematycy i przyrodnicy nie rezygnują całkowicie ze stosowania miary stopniowej.
Kąty wierzchołkowe i przyległe
Zapoznaj się z przykładem zawartym w poniższym aplecie.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DqIN54whO
Zapoznaj się z przykładem zawartym w poniższym aplecie
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DqIN54whO
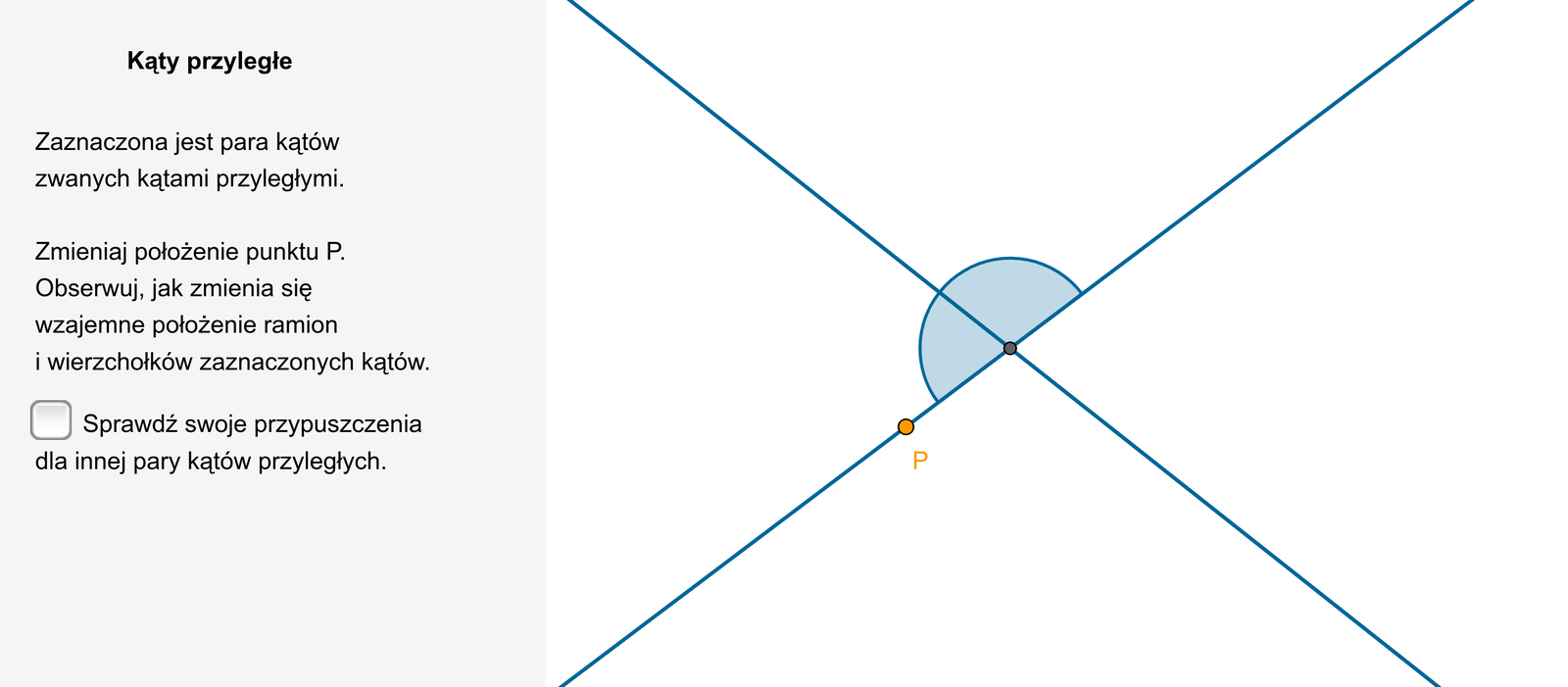
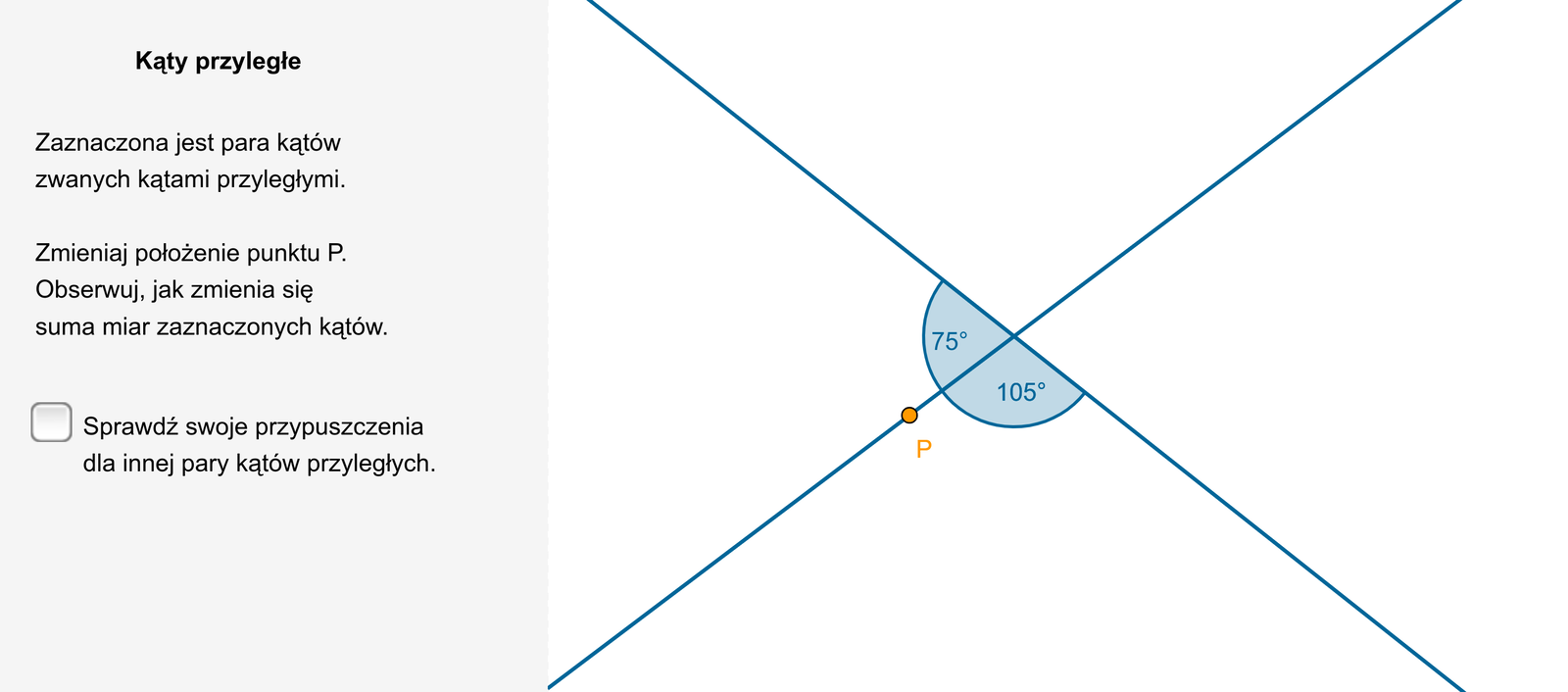
Kąty przyległe to dwa kąty wypukłe, które mają jedno ramię wspólne, a pozostałe ramiona dopełniają się do prostej.
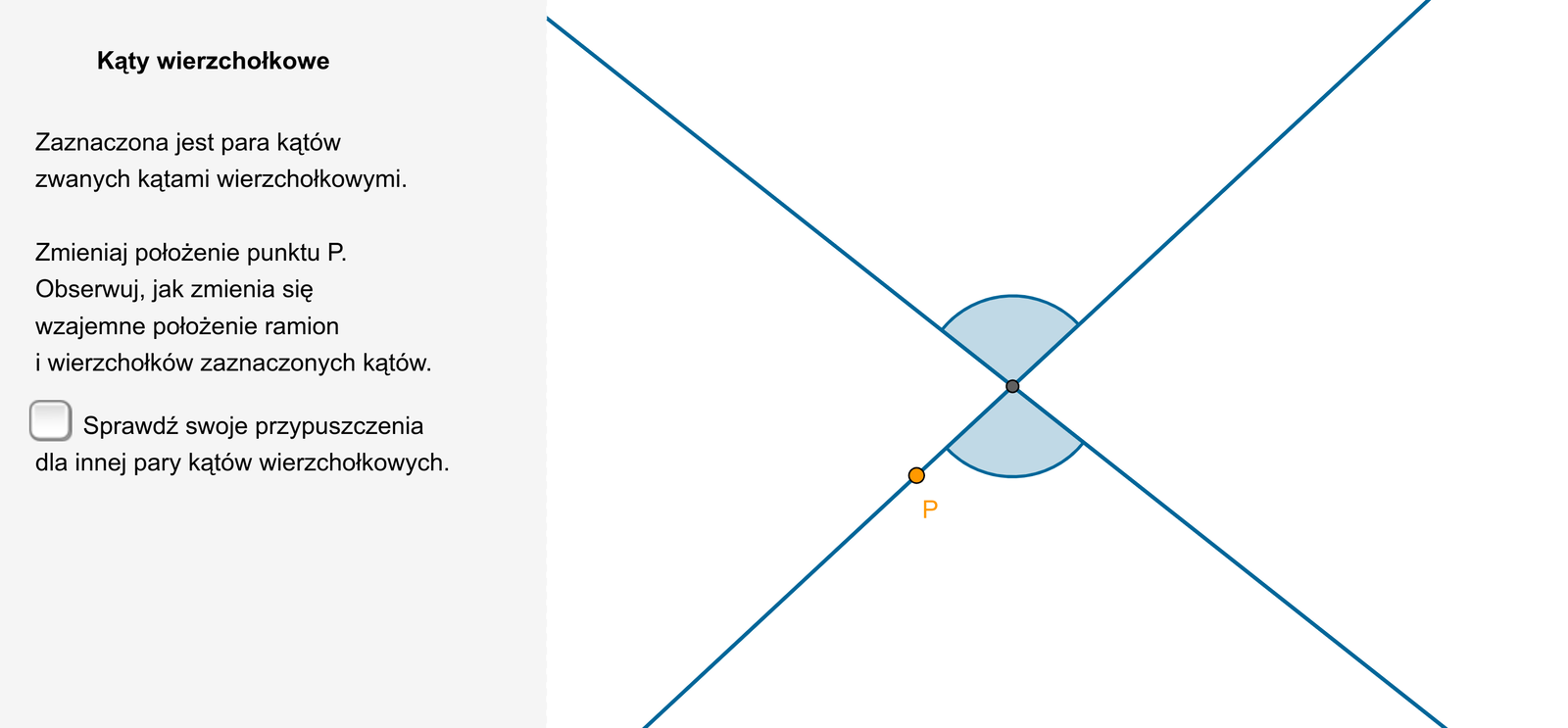
Kąty wierzchołkowe to dwa kąty wypukłe, które mają wspólny wierzchołek i przedłużeniem ramion jednego kąta są odpowiednie ramiona drugiego kąta.
R5pEX3r0V622H1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Na przykład i na rysunku są kątami przyległymi. Pary kątów wierzchołkowych to i oraz i .
Zapoznaj się z przykładem zawartym w poniższym aplecie.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DqIN54whO
Suma miar kątów przyległych jest równa .
Zapoznaj się z przykładem zawartym w poniższym aplecie.
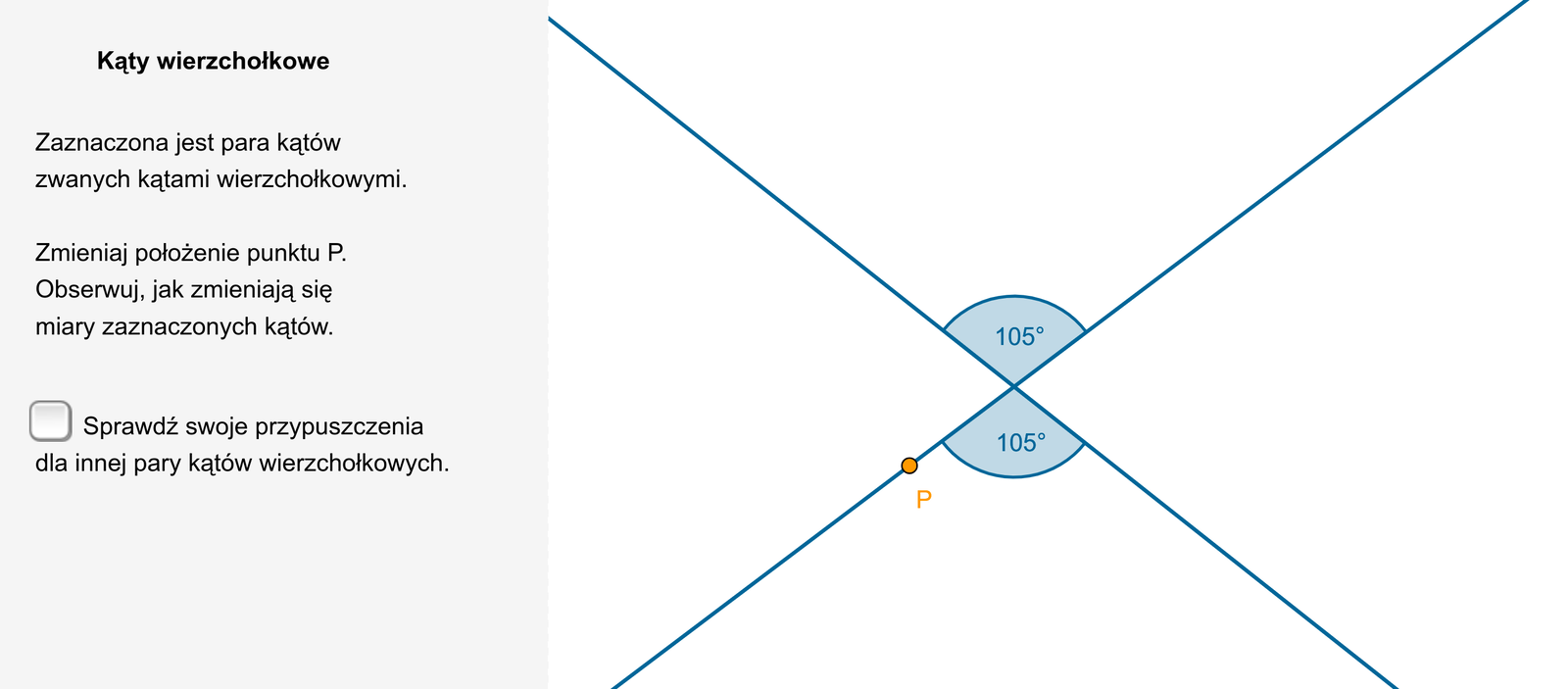
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DqIN54whO
Kąty wierzchołkowe mają równe miary.
Dowód:
Wprost z twierdzenia o sumie miar kątów przyległych wynika, że
oraz
Stąd . Wynika stąd, że kąty wierzchołkowe są równe.
Obliczmy miary kątów , i zaznaczonych na rysunku.
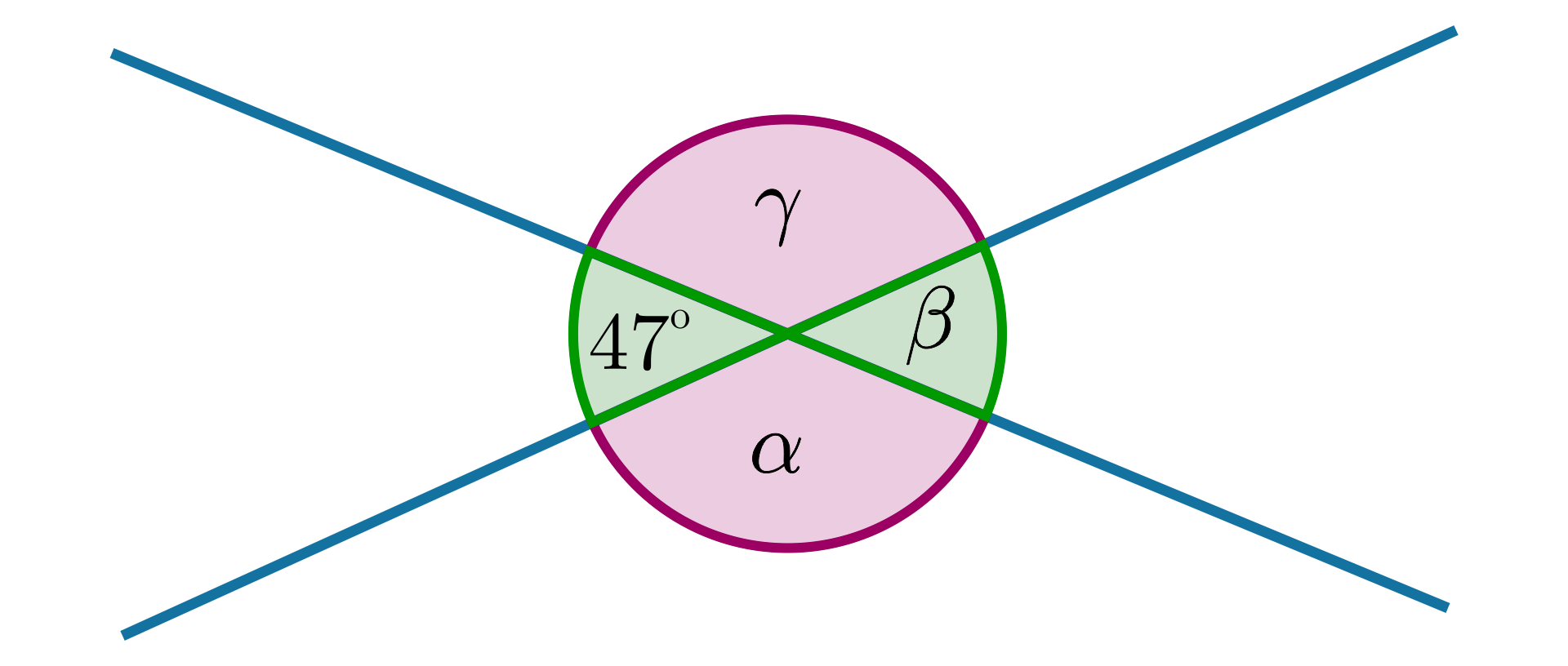
Kąty o miarach i to kąty wierzchołkowe, więc . Każdy z kątów i jest przyległy do kąta o mierze . Zatem
Wyznaczymy miary kątów równoległoboku .

Rozwiązanie:
Kąty i to kąty wierzchołkowe, mają więc równe miary.
Suma kątów równoległoboku leżących przy jednym boku jest równa .
Kąty i leżą przy jednym boku.
W równoległoboku kąty leżące naprzeciw siebie mają równe miary.
Kąt leży naprzeciw kąta , kąty te mają więc równe miary.
Podobnie kąt leży naprzeciw kąta , kąty te mają równe miary.
Odpowiedź: Miary kątów równoległoboku są równe: , , , .
Zapoznaj się z animacją, pokazującą porównywanie kątów.

Film dostępny pod adresem /preview/resource/R9ncwkBcQcxZS
Animacja o porównywaniu kątów.
Zapoznaj się z przykładem zawartym w poniższym aplecie.
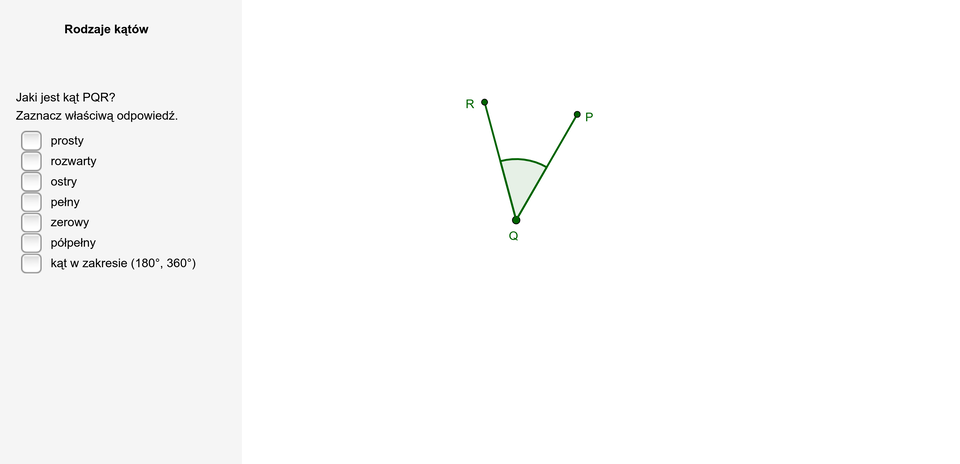
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DqIN54whO
- Kąt półpełny jest kątem ostrym.
- Kąty przyległe mają równe miary.
- Kąty wierzchołkowe mają równe miary.
- Kąt prosty jest kątem wypukłym.
Zapoznaj się z poniższym rysunkiem.

- i
- i
- i
- i
Narysuj romb. Podaj miary kątów wierzchołkowych oraz przyległych, jakie tworzą przekątne w tym rombie.
Wyobraź sobie dowolny romb. Podaj miary kątów wierzchołkowych oraz przyległych, jakie tworzą przekątne w tym rombie.
Zapoznaj się z poniższym rysunkiem. Oblicz miary kątów , , .

Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.