3. Losowanie bez zwracania

RrOCpVV4ZVTid

RNBVAlfRrNgY91

Ilustracja przedstawia rycerzy okrągłego stołu. Mężczyźni w płaszczach oraz koronach. Jeden z nich stoi. — Rycerze Okrągłego Stołu i święty Graal. Malunek z XV w.
Źródło: dostępny w internecie: commons.wikimedia.org, domena publiczna.

Czy jadąc windą z kilkoma osobami zdarzyło ci się zastanawiać na ile sposobów mogą wysiąść na różnych piętrach te osoby? A może znajomi, którzy przyszli do ciebie na imieniny i siadali przy okrągłym stole, zadali ci pytanie – na ile sposobów mogą to zrobić?

Po zapoznaniu się z tym materiałem, na pewno bez problemu odpowiesz na podobne pytania.

W życiu codziennym przeprowadzamy wiele doświadczeń. Jeżeli myślimy o kombinatoryce to mamy do czynienia z doświadczeniami losowymi.

Doświadczenie losowedoświadczenie losoweDoświadczenie losowe, to doświadczenie, które może być powtarzane dowolnie wiele razy w identycznych (lub zbliżonych) warunkach, które ma kilka możliwych wyników i którego wyniku nie daje się jednoznacznie przewidzieć.

W obliczeniach wykorzystamy regułę mnożenia.

reguła mnożenia

Definicja: reguła mnożenia

Zasada, za pomocą której określa się liczbę wszystkich możliwych wyników doświadczenia, polegającego na wykonaniu po kolei czynności, z których pierwsza może zakończyć się na jeden z $k_{1}$ sposobów, druga – na jeden z $k_{2}$ sposobów, trzecia – na jeden z $k_{3}$ sposobów i tak dalej do tej czynności, która może zakończyć się na jeden z $k_{n}$ sposobów. Liczba ta jest równa $k_{1} \cdot k_{2} \cdot k_{3} \cdot \dots \cdot k_{n}$ .

Załóżmy, że mamy do dyspozycji $6$ poziomych pasów o różnych barwach. Na ile różnych sposobów można utworzyć z tych pasów flagę składającą się z trzech poziomych pasów?

RjMhMpYCTf7Jw

Ilustracja przedstawia sześć pasków w różnych kolorach. Kolory tych pasków to: czarny, czerwony, żółty, zielony, biały i niebieski. — Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

R18dJgdpZtioO

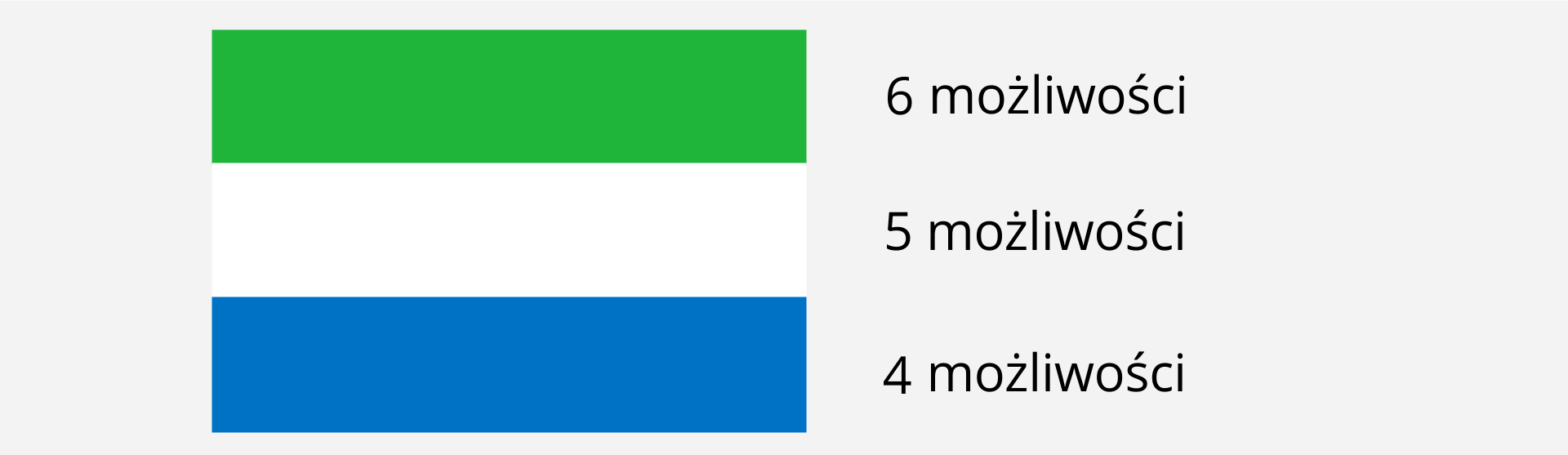
Ilustracja przedstawia flagę złożoną z trzech pasków o różnych kolorach. Przy dolnym pasku widnieje napis: 6 możliwości, przy środkowym pasku widnieje napis: 5 możliwości, a przy górnym pasku widnieje napis: 4 możliwości. — Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Zauważmy, że mamy konkretną liczbę możliwości wyboru koloru dla poszczególnych pasów, wynikającą z poprzednich wyborów, więc:

kolor pierwszego pasa możemy wybrać na $6$ sposobów, spośród sześciu dostępnych pasów,
kolor drugiego pasa możemy wybrać na $5$ sposobów, spośród pięciu pozostałych pasów,
kolor trzeciego pasa możemy wybrać na $4$ sposoby, spośród czterech pozostałych pasów.

Zatem liczba możliwych ustawień kolorów w trzypasmowej fladze wynosi:

$6 \cdot 5 \cdot 4 = 120$ .

W opisanym przykładzie mamy do czynienia z losowaniem bez zwracania.

Zwróćmy uwagę, że jest to rodzaj wielokrotnego losowania, w którym wylosowane elementy nie trafiają z powrotem do puli.

Przykładami losowania bez zwracania są np.:

losowanie po kolei kilku kul z urny, przy czym wylosowanych kul nie wrzucamy z powrotem do urny,
wybór przewodniczącego, zastępcy oraz skarbnika klasowego z grupy klasowej, czyli losowanie kolejnych osób do wskazanych funkcji,
rozmieszczanie osób w pokojach hotelowych, przy czym do każdego pokoju przydzielamy tylko jedną osobę, czyli losowanie kolejnych pokoi dla gości lub losowanie kolejnych osób do wskazanych pokoi.

W poniższych przykładach omówimy kilka zastosowań losowania bez zwracania w różnych doświadczeniach losowych.

Przykład 1

Kod do walizki tworzymy z trzech liter wybranych spośród następujących: $A$ , $B$ , $C$ , $D$ , $E$ , $F$ , $G$ , $H$ , $I$ , $J$ , $K$ , przy czym litery nie mogą się powtarzać. Obliczymy, ile jest takich kodów.

Rozwiązanie:

Zauważmy, że na pierwszym miejscu kodu możemy wpisać jedną z jedenastu liter, na drugim - jedną z pozostałych dziesięciu, a na trzecim - jedną z pozostałych dziewięciu.

Wobec tego liczba wszystkich możliwych kodów jest równa:

$11 \cdot 10 \cdot 9 = 990$ .

Przykład 2

Z pojemnika, w którym znajduje się $15$ kul, w tym $7$ białych i $8$ czarnych losujemy dwie kule bez zwracania. Obliczymy, ile jest możliwości wylosowania kul w różnych kolorach.

Rozwiązanie:

Przedstawmy rozwiązania zadania za pomocą drzewa. Niech $B$ oznacza kulę białą, a $C Z$ kulę czarną.

RVFPfaUoELAOp

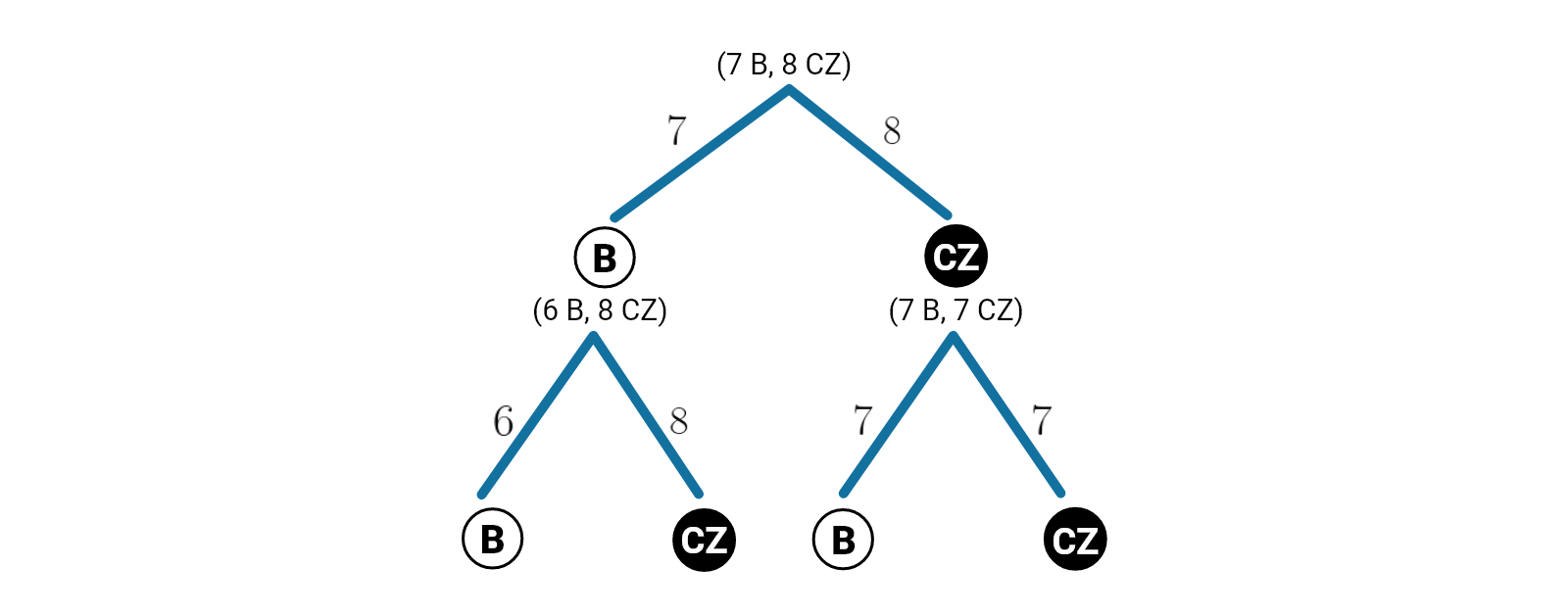
Ilustracja — Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

W poniższym schemacie przedstawiono drzewko stochastyczne ilustrujące możliwości wylosowania czarnej i białej kuli w dwóch kolejnych losowaniach bez zwracania. Literą B oznaczono sytuację, w której wylosowana kula ma kolor biały, natomiast literami C Z oznaczono sytuację, w której wylosowana kula ma kolor czarny. Lista elementów:

Nazwa kategorii: START
Na tym etapie jest 7 kul białych i 8 kul czarnych.
Elementy należące do kategorii START
- Nazwa kategorii: B ( $I$ losowanie).
  Na tym etapie jest 6 kul białych i 8 kul czarnych.
  Elementy należące do kategorii B ( $I$ losowanie)
  - Nazwa kategorii: B ( $II$ losowanie).
  - Nazwa kategorii: C Z ( $II$ losowanie).
- Nazwa kategorii: C Z ( $I$ losowanie). Na tym etapie jest 7 kul białych i 7 kul czarnych.
  Elementy należące do kategorii C Z ( $I$ losowanie)
  - Nazwa kategorii: B ( $II$ losowanie).
  - Nazwa kategorii: C Z ( $II$ losowanie).

Ponieważ interesuje nas wylosowanie kul w różnych kolorach, zatem do rozwiązania zadania bierzemy dwie możliwości:

Ze wszystkich kul wylosujemy najpierw kulę białą, a z pozostałych kulę czarną. Takich możliwości jest:
$7 \cdot 8 = 56$ .
Ze wszystkich kul wylosujemy najpierw kulę czarną, a z pozostałych kulę białą. Takich możliwości jest:
$8 \cdot 7 = 56$ .

Wobec tego, stosując regułę dodawania, liczba wszystkich możliwych wyników doświadczenia losowego, polegającego na wylosowaniu kul w różnych kolorach wynosi:

$7 \cdot 8 + 8 \cdot 7 = 56 + 56 = 112$ .

Przykład 3

Obliczymy, ile jest:

wszystkich liczb trzycyfrowych, w których zapisie nie występuje cyfra zero i cyfry się nie powtarzają,
wszystkich liczb pięciocyfrowych o niepowtarzających się cyfrach, jeśli pierwsza cyfra jest parzysta, a pozostałe są nieparzyste.

Rozwiązanie:

Ponieważ w rozpatrywanych liczbach nie występuje cyfra $0$ , zatem wszystkich liczb trzycyfrowych, w których cyfry się nie powtarzają jest:
$9 \cdot 8 \cdot 7 = 504$ .
W rozpatrywanych liczbach pierwsza cyfra musi być parzysta, zatem możemy je wybrać spośród $4$ cyfr: $2$ , $4$ , $6$ , $8$ .

Następne cztery cyfry muszą być nieparzyste, więc wybieramy je spośród cyfr: $1$ , $3$ , $5$ , $7$ , $9$ . Ponieważ cyfry się nie powtarzają, zatem takich wyborów jest:

$5 \cdot 4 \cdot 3 \cdot 2 = 120$ .

Zatem wszystkich rozważanych liczb pięciocyfrowych jest:

$4 \cdot 5 \cdot 4 \cdot 3 \cdot 2 = 480$ .

Przykład 4

Do windy zatrzymującej się na $8$ piętrach wsiadły $3$ osoby. Obliczymy, na ile sposobów te osoby mogą opuścić windę, jeśli każda z nich wysiada:

na innym piętrze,
na innym piętrze i nikt nie wysiada na dwóch ostatnich piętrach.

Rozwiązanie:

Jeżeli każda z osób wysiada na innym piętrze, to liczba sposobów, na które te osoby mogą opuścić windę wynosi:
$8 \cdot 7 \cdot 6 = 336$ .
Jeżeli każda z osób wysiada na innym piętrze i nikt nie wysiada na piętrach $7$ i $8$ , to liczba sposobów, na które te osoby mogą opuścić windę wynosi:
$6 \cdot 5 \cdot 4 = 120$ .

Przykład 5

W konkursie matematycznym wzięło udział $50$ uczestników. Przyznawane są tylko miejsca od $I$ do $III$ . Obliczymy, ile jest możliwości przyznania trzech miejsc w tym konkursie.

Rozwiązanie:

Ponieważ w konkursie przyznaje się miejsca $I$ , $II$ oraz $III$ , zatem $I$ miejsce może zdobyć jeden z $50$ uczestników, $II$ miejsce zdobędzie jeden z pozostałych $49$ , a $III$ - jeden z pozostałych $48$ uczestników. Wobec tego liczba wszystkich możliwości przyznania trzech miejsc jest równa:

$50 \cdot 49 \cdot 48 = 117600$ .

Notatnik

R1KmIqiPdxbI4

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Prezentacja multimedialna

Obejrzyj prezentację multimedialną, a następnie wykonaj poniższe polecenia.

RHfNW66FGu3It

R1PAtB41UieMA

Transkrypcjaazurewhite

RwMi8fDUmkAbR

R9M8Z8ed1q3lq

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

RHNKbCBgEkKrZ

R1eK64KmjJ8n9

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Ile jest wszystkich liczb trzycyfrowych, w których zapisie wstępują tylko cyfry $1, 2, 3, 4, 5$ i cyfry się nie powtarzają?

R1Nk4GjYdECYy

RtZkwXLrRUezw

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Na ile sposobów $32$ – osobowa klasa może wybrać trzy różne osoby do zajmowania stanowisk przewodniczącego, zastępcy przewodniczącego oraz skarbnika?

R1HZJxiVWz0K7

RLiQ8WT7I2wiA

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Do windy zatrzymującej się na $12$ piętrach wsiadły $4$ osoby o imionach zaczynających się na litery A, B, C, D. Na ile sposobów te osoby mogą opuścić windę, jeżeli każda z nich wysiada na innym piętrze i osoby te wysiadają w kolejności A, B, C, D?

RGetlkZfvIW2Z

RAUO3nN7ZUWoJ

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Do windy zatrzymującej się na $12$ piętrach wsiadły $4$ osoby: A, B, C, D. Na ile sposobów te osoby mogą opuścić windę, jeżeli każda z nich wysiada na innym piętrze i nikt nie wysiada na pierwszych dwóch piętrach?

RzGfOQn4CeIjf

RROCjvwtJlpHV

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Ile można utworzyć kodów składających się z $5$ różnych liter, w których mogą występować litery: A, B, C, D, E, F i żadna litera się nie powtarza?

R1ZP0c6BvYaLy

Ru80GwBePBUow

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Ile można utworzyć kodów trzyliterowych, w których może wystąpić każda z $26$ liter alfabetu i żadna litera się nie powtarza?

RwdsymCpYtfkK

RkdC3PBrniQSd

Transkrypcjaazurewhite

RGYdkSrtKA7X8

R12hCNzw2uTKt

Transkrypcjaazurewhite

W pojemniku znajduje się $10$ kul białych oraz $6$ kul czarnych. Losujemy kolejno $2$ kule bez zwracania. Wyznaczymy, ile jest możliwych wyników losowania, jeżeli wylosujemy co najmniej jedną kulę białą.

Przedstawmy liczbę możliwych wyników za pomocą drzewa, w którym każdy poziom oznacza jedno losowanie.

R1EQJtX4DwGp3

RbFNgVKkuPKhH

Transkrypcjaazurewhite

W pojemniku znajduje się $12$ kul białych oraz $10$ kul czarnych. Losujemy kolejno $2$ kule bez zwracania. Wyznaczymy, ile jest możliwych wyników losowania, jeżeli wylosujemy kule tego samego koloru.

Przedstawmy liczbę możliwych wyników za pomocą drzewa, w którym każdy poziom oznacza jedno losowanie.

RvRgS6LFrhLcb

RtdYRGkYs9Vii

Transkrypcjaazurewhite

W pojemniku znajduje się $4$ kule białych oraz $5$ kul czarnych. Losujemy kolejno $3$ kule bez zwracania. Wyznaczymy, ile jest możliwych wyników losowania, jeżeli wylosujemy kule tego samego koloru.

Przedstawmy rozwiązanie zadania za pomocą drzewa, w którym kolejne poziomy oznaczają jedno losowanie.

RE0jFItjIJRr3

RijGej6MrRxc4

Transkrypcjaazurewhite

W pojemniku znajduje się $5$ kul białych oraz $6$ kul czarnych. Losujemy kolejno $3$ kule bez zwracania. Wyznaczymy, ile jest możliwych wyników losowania, jeżeli wylosujemy dokładnie jedną kulę białą.

Przedstawmy rozwiązanie zadania za pomocą drzewa, w którym kolejne poziomy oznaczają jedno losowanie.

Rbcp8p9MxHoEq

R1eynJN7BKB2d

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Przeanalizuj działanie schematu interaktywnego dotyczącego losowania kolejno $3$ kul bez zwracania przy zadanym warunku.

Slajd pierwszy:

Na tle z rozsypanymi liczbami zapisano tytuł prezentacji: Losowanie bez zwracania.

Slajd drugi:

Przykład pierwszy.

Ile jest liczb trzycyfrowych, w których cyfry się nie powtarzają?

Rozwiązanie:
Cyfra setek – dziewięć możliwości, ponieważ wybieramy jedną cyfrę bez cyfry zero, cyfra dziesiątek – dziewięć możliwości, ponieważ wybieramy jedną z pozostałych dziewięciu cyfr. Cyfra jedności - osiem możliwości ponieważ wybieramy jedną z pozostałych ośmiu cyfr. Razem jest to dziewięć razy dziewięć razy osiem równa się sześćset czterdzieści osiem.

Odpowiedź:
Jest sześćset czterdzieści osiem liczb trzycyfrowych, w których cyfry się nie powtarzają.

Slajd trzeci:

Przykład drugi.

Ile jest wszystkich liczb trzycyfrowych, w których zapisie występują tylko cyfry jeden, dwa, trzy, cztery, pięć i cyfry się nie powtarzają? Cyfra setek – pięć możliwości, ponieważ wybieramy jedną cyfrę z cyfr jeden, dwa, trzy, cztery, pięć , cyfra dziesiątek – cztery możliwości, ponieważ wybieramy jedną z czterech pozostałych cyfr. Cyfra jedności – trzy możliwości, ponieważ wybieramy z trzech pozostałych cyfr. Razem jest to pięć razy cztery razy trzy równa się sześćdziesiąt.

Odpowiedź:
Jest sześćdziesiąt liczb trzycyfrowych, w których zapisie cyfry się nie powtarzają i w zapisie występują tylko cyfry jeden, dwa, trzy, cztery, pięć.

Slajd czwarty:

Przykład trzeci.

Na ile sposobów trzydziestu dwu osobowa klasa może wybrać trzy różne osoby do zajmowania stanowisk przewodniczącego, zastępcy przewodniczącego oraz skarbnika?

Rozwiązanie:
Wybór przewodniczącego – trzydzieści dwie możliwości, ponieważ wybieramy jedną osobę z trzydziestu dwóch. Wybór zastępcy przewodniczącego – trzydzieści jeden możliwości, ponieważ wybieramy jedną osobę z pozostałych trzydziestu jeden osób, Wybór skarbnika – trzydzieści możliwości, ponieważ wybieramy jedną osobę z pozostałych trzydziestu osób. Razem jest to trzydzieści dwa razy trzydzieści jeden razy trzydzieści równa się dwadzieścia dziewięć tysięcy sześćset siedemdziesiąt.

Odpowiedź:
Jest dwadzieścia dziewięć tysięcy sześćset siedemdziesiąt różnych możliwości wyboru przewodniczącego, zastępcy przewodniczącego oraz skarbnika.

Slajd piąty:

Przykład czwarty.

Do windy zatrzymującej się na dwunastu piętrach wsiadły cztery osoby o imionach zaczynających się na litery A, B, C, D. Na ile sposobów te osoby mogą opuścić windę, jeżeli każda z nich wysiada na innym piętrze i osoby te wysiadają w kolejności A, B, C, D?

Osoba A ma dwanaście możliwości wyboru piętra, Osoba B ma jedenaście możliwości wyboru piętra, Osoba C ma dziesięć możliwości wyboru piętra oraz Osoba D ma dziewięć możliwości wyboru piętra. Razem to jest dwanaście razy jedenaście razy dziesięć razy dziewięć równa się jedenaście tysięcy osiemset osiemdziesiąt.

Odpowiedź:
Jest jedenaście tysięcy osiemset osiemdziesiąt różnych sposobów, na które 4 osoby o imionach zaczynających się na litery A, B, C, D mogą opuścić windę, jeżeli każda z nich wysiada na innym piętrze i osoby te wysiadają w kolejności A, B, C, D.

Slajd szósty:

Przykład piąty.

Do windy zatrzymującej się na dwunastu piętrach wsiadły cztery osoby: A, B, C, D. Na ile sposobów te osoby mogą opuścić windę, jeżeli każda z nich wysiada na innym piętrze i nikt nie wysiada na pierwszych dwóch piętrach?

Rozwiązanie:
Osoba A ma dziesięć możliwości wyboru piętra, bez piętra pierwszego i drugiego, Osoba B ma dziewięć możliwości wyboru piętra, Osoba C ma osiem możliwości wyboru piętra oraz Osoba D ma siedem możliwości wyboru piętra. Razem to jest dziesięć razy dziewięć razy osiem razy siedem równa się pięć tysięcy czterdzieści.

Odpowiedź:
Jest pięć tysięcy czterdzieści. różnych sposobów, na które cztery osoby A, B, C, D mogą opuścić windę, jeżeli każda z nich wysiada na innym piętrze i nikt nie wysiada na pierwszych dwóch piętrach.

Slajd siódmy:

Przykład szósty.

Ile można utworzyć kodów składających się z pięciu różnych liter, w których mogą występować litery: A, B, C, D, E, F i żadna litera się nie powtarza?

Rozwiązanie:
Na pierwszym miejscu możemy umieścić jedną z sześciu liter: A, B, C, D, E, F, na drugim miejscu możemy umieścić jedną z pięciu pozostałych liter, na trzecim miejscu możemy umieścić jedną z czterech pozostałych liter, na czwartym miejscu możemy umieścić jedną z trzech z pozostałych liter, na piątym miejscu możemy umieścić jedną z dwóch pozostałych liter. Razem jest to sześć razy pięć razy cztery razy trzy razy dwa równa się siedemset dwadzieścia.

Odpowiedź:
Można utworzyć siedemset dwadzieścia kodów pięcioliterowych o różnych literach ze zbioru liter: A, B, C, D, E, F.

Slajd ósmy:

Przykład siódmy.

Ile można utworzyć kodów trzyliterowych, w których może wystąpić każda z dwudziestu sześciu liter liter alfabetu i żadna litera się nie powtarza?

Rozwiązanie:
Na pierwszym miejscu możemy umieścić jedną z dwudziestu sześciu liter

Na drugim miejscu możemy umieścić jedną z dwadzieścia pięć pozostałych liter.

Na trzecim miejscu możemy umieścić jedną z dwudziestu czterech pozostałych liter.

Razem jest to dwadzieścia sześć razy dwadzieścia pięć razy dwadzieścia cztery równa się piętnaście tysięcy sześćset.

Odpowiedź:
Można utworzyć piętnaście tysięcy sześćset kodów trzyliterowych o różnych literach ze zbioru dwudziestu sześciu liter.

Slajd dziewiąty:

Przykład ósmy.

Losujemy dwie liczby ze zbioru liczb pierwszych mniejszych od trzydziestu. Ile jest możliwych wyników w przypadku losowania bez zwracania?

Rozwiązanie:
Liczby pierwsze mniejsze od trzydziestu: dwa, trzy, pięć, ,siedem, jedenaście, trzynaście, siedemnaście, dziewiętnaście, dwadzieścia trzy, dwadzieścia dziewięć. Jest dziesięć liczb pierwszych mniejszych od trzydziestu. Liczba możliwych wyników wylosowania pierwszej liczby jest równa dziesięć, a liczba możliwych wyników wylosowania drugiej liczby jest równa dziewięć. Razem jest to dziesięć razy dziewięć równa się dziewięćdziesiąt.

Odpowiedź:
Jest dziewięćdziesiąt możliwych wyników.

Slajd dziesiąty:

Przykład dziewiąty.

W pojemniku znajduje się dziesięć kul białych oraz sześć kul czarnych. Losujemy dwie kule bez zwracania. Wyznaczymy, ile jest możliwych wyników losowania, jeżeli wylosujemy co najmniej jedną kulę białą.

Rozwiązanie:
Przedstawmy liczbę możliwych wyników za pomocą drzewa, w którym każdy poziom oznacza jedno losowanie.

Nazwa kategorii: START
Na tym etapie jest dziesięć kul białych i sześć kul czarnych.
Elementy należące do kategorii START
- Nazwa kategorii: B ( $I$ losowanie).
- Nazwa kategorii: C Z ( $I$ losowanie)
Elementy należące do kategorii B ( $I$ losowanie). Na tym etapie jest dziewięć kul białych i sześć kul czarnych
- Nazwa kategorii: B ( $II$ losowanie).
- Nazwa kategorii: C Z ( $II$ losowanie).
Elementy należące do kategorii C Z ( $I$ losowanie). Na tym etapie jest dziesięć kul białych i pięć kul czarnych.
- Nazwa kategorii: B ( $II$ losowanie).
- Nazwa kategorii: C Z ( $II$ losowanie).

Liczba wszystkich wyników losowania co najmniej jednej kuli białej wynosi $10 \cdot 9 + 10 \cdot 6 + 6 \cdot 10 = 90 + 60 + 60 = 210$ .

Slajd jedenasty:

Przykład dziesiąty.

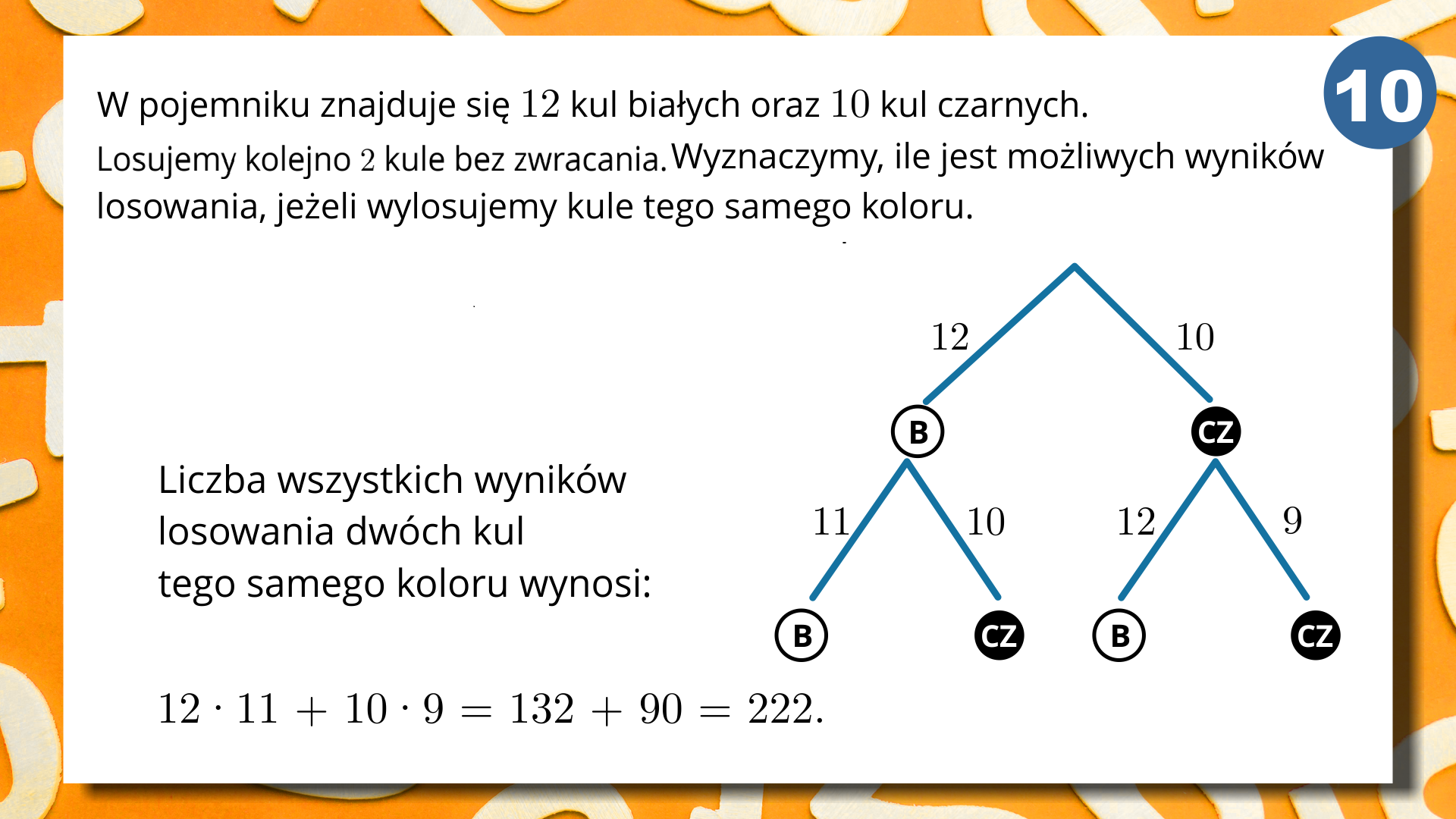
W pojemniku znajduje się dwanaście kul białych oraz dziesięć kul czarnych. Losujemy dwie kule bez zwracania. Wyznaczymy, ile jest możliwych wyników losowania, jeżeli wylosujemy kule tego samego koloru.

Rozwiązanie:
Przedstawmy liczbę możliwych wyników za pomocą drzewa, w którym każdy poziom oznacza jedno losowanie.

Nazwa kategorii: START
Na tym etapie jest dwanaście kul białych i dziesięć kul czarnych..
Elementy należące do kategorii START
- Nazwa kategorii: B ( $I$ losowanie).
- Nazwa kategorii: C Z ( $I$ losowanie)
Elementy należące do kategorii B ( $I$ losowanie). Na tym etapie jest jedenaście kul białych i dziesięć kul czarnych.
- Nazwa kategorii: B ( $II$ losowanie).
- Nazwa kategorii: C Z ( $II$ losowanie).
Elementy należące do kategorii C Z ( $I$ losowanie). Na tym etapie jest dwanaście kul białych i dziewięć kul czarnych.
- Nazwa kategorii: B ( $II$ losowanie).
- Nazwa kategorii: C Z ( $II$ losowanie).

Liczba wszystkich wyników losowania dwóch kul tego samego koloru wynosi $12 \cdot 11 + 10 \cdot 9 = 132 + 90 = 222$ .

Slajd dwunasty:

Przykład jedenasty.

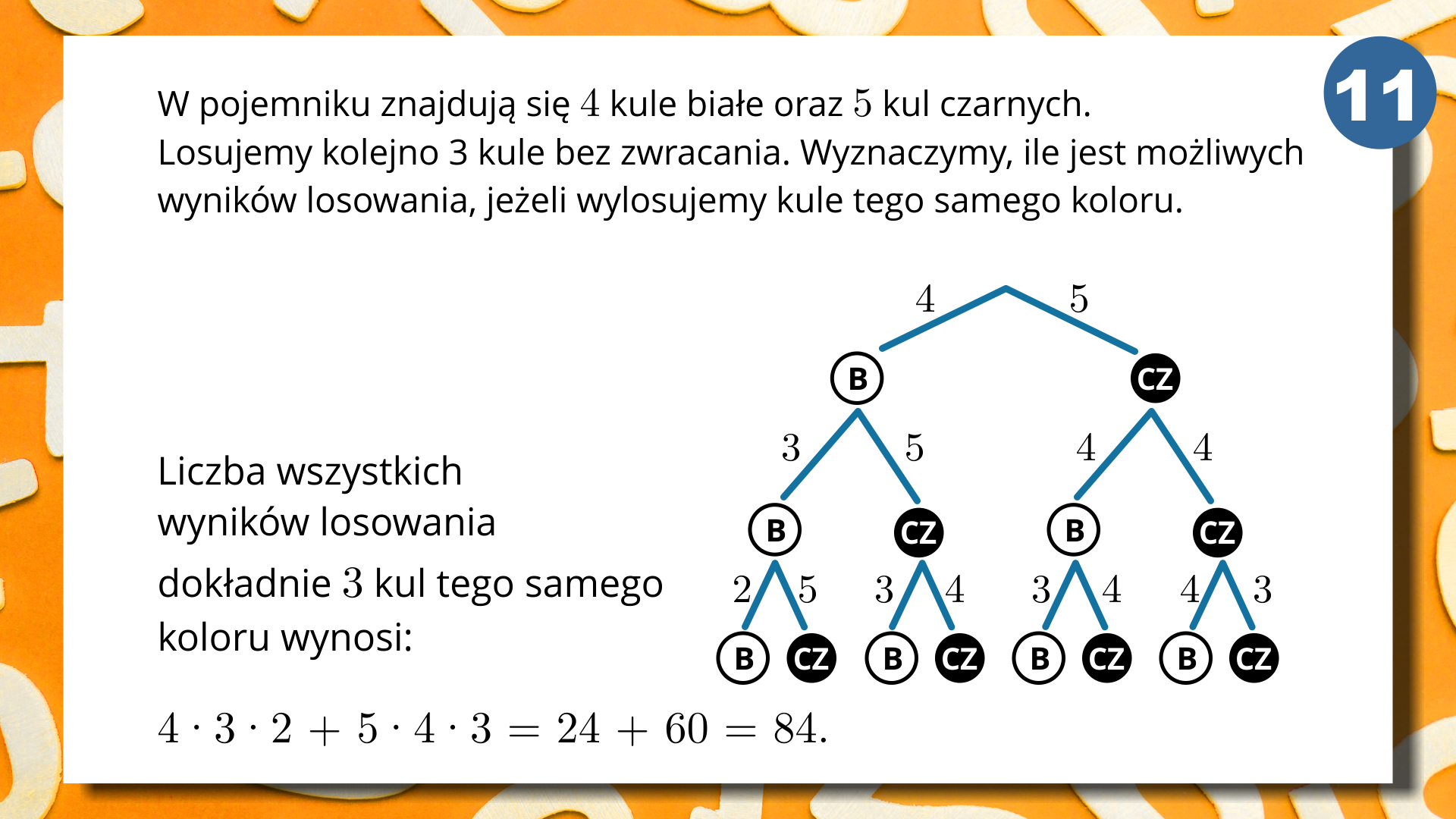
W pojemniku znajdują się 4 kule białe oraz 5 kul czarnych. Losujemy 3 kule bez zwracania. Wyznaczymy, ile jest możliwych wyników losowania, jeżeli wylosujemy kule tego samego koloru.

Rozwiązanie:
Przedstawmy rozwiązanie zadania za pomocą drzewa, w którym kolejne poziomy oznaczają jedno losowanie.

Nazwa kategorii: START
Na tym etapie są cztery kule białe i pięć czarnych.
Elementy należące do kategorii START
- Nazwa kategorii: B ( $I$ losowanie).
- Nazwa kategorii: C Z ( $I$ losowanie)
Elementy należące do kategorii B ( $I$ losowanie). Na tym etapie są trzy kule białe i pięć czarnych.
- Nazwa kategorii: B ( $II$ losowanie).
- Nazwa kategorii: C Z ( $II$ losowanie).
Elementy należące do kategorii B ( $II$ losowanie). Na tym etapie są dwie kule białe i pięć czarnych.
- Nazwa kategorii: B ( $III$ losowanie).
- Nazwa kategorii: C Z ( $III$ losowanie).
Elementy należące do kategorii C Z ( $II$ losowanie). Na tym etapie są trzy kule białe i cztery czarne.
- Nazwa kategorii: B ( $III$ losowanie).
- Nazwa kategorii: C Z ( $III$ losowanie).
Elementy należące do kategorii C Z ( $I$ losowanie). Na tym etapie są cztery kule białe i cztery czarne.
- Nazwa kategorii: B ( $II$ losowanie).
- Nazwa kategorii: C Z ( $II$ losowanie).
Elementy należące do kategorii B ( $II$ losowanie). Na tym etapie są trzy kule białe i cztery czarne.
- Nazwa kategorii: B ( $III$ losowanie).
- Nazwa kategorii: C Z ( $III$ losowanie).
Elementy należące do kategorii C Z ( $II$ losowanie). Na tym etapie są cztery kule białe i trzy czarne.
- Nazwa kategorii: B ( $III$ losowanie).
- Nazwa kategorii: C Z ( $III$ losowanie).

Liczba wszystkich wyników losowania dokładnie 3 kul tego samego koloru wynosi: $4 \cdot 3 \cdot 2 + 5 \cdot 4 \cdot 3 = 24 + 60 = 84$ .

Slajd trzynasty:

Przykład dwunasty.

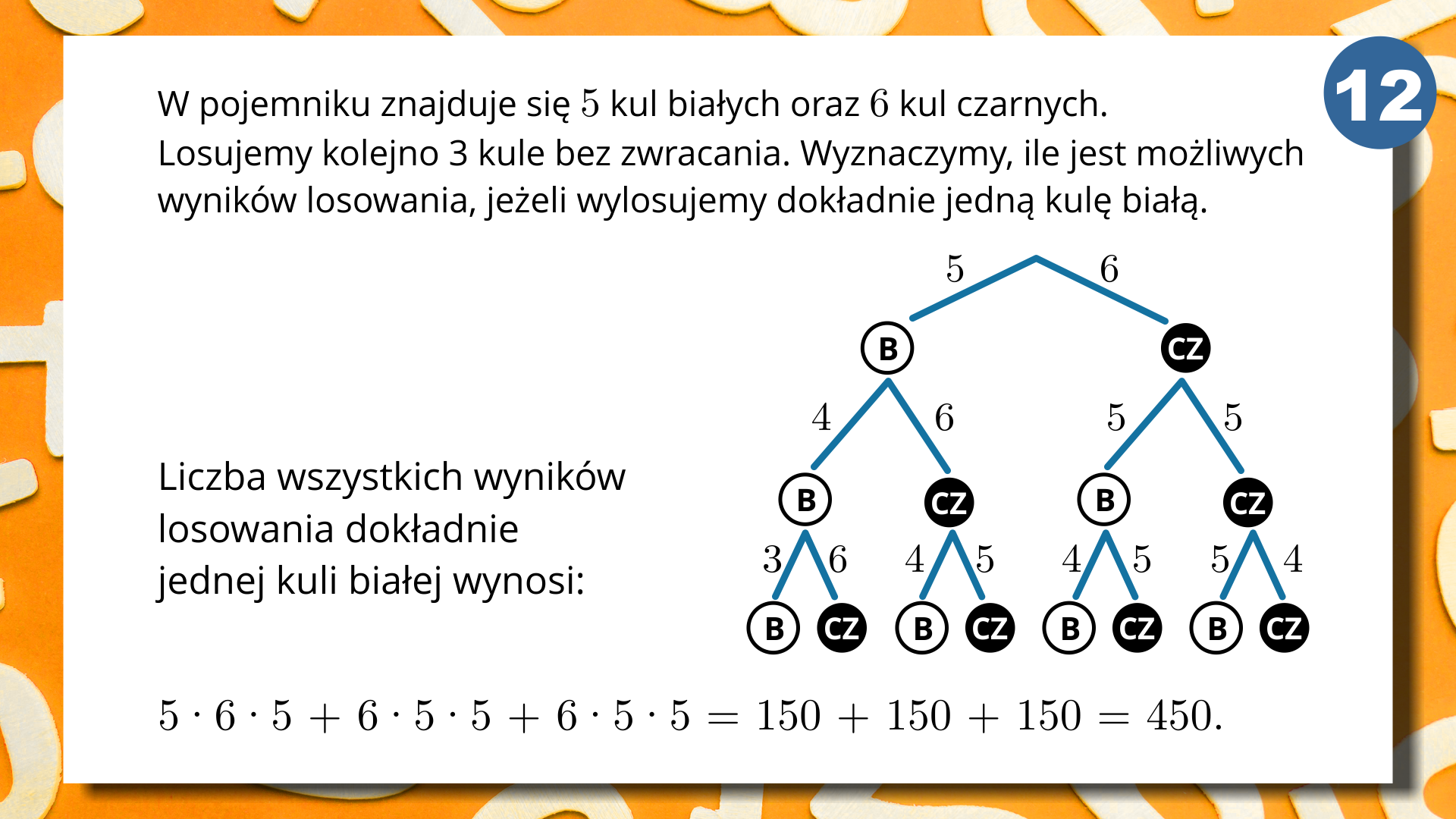
W pojemniku znajdują się pięć kul białych oraz sześć kul czarnych. Losujemy trzy kule bez zwracania. Wyznaczymy, ile jest możliwych wyników losowania, jeżeli wylosujemy kule tego samego koloru.

Rozwiązanie:
Przedstawmy rozwiązanie zadania za pomocą drzewa, w którym kolejne poziomy oznaczają jedno losowanie.

Nazwa kategorii: START
Na tym etapie jest pięć kul białych oraz sześć kul czarnych.
Elementy należące do kategorii START
- Nazwa kategorii: B ( $I$ losowanie).
- Nazwa kategorii: C Z ( $I$ losowanie)
Elementy należące do kategorii B ( $I$ losowanie). Na tym etapie są cztery kule białe i sześć czarnych.
- Nazwa kategorii: B ( $II$ losowanie).
- Nazwa kategorii: C Z ( $II$ losowanie).
Elementy należące do kategorii B ( $II$ losowanie). Na tym etapie są trzy kule białe i sześć czarnych.
- Nazwa kategorii: B ( $III$ losowanie).
- Nazwa kategorii: C Z ( $III$ losowanie).
Elementy należące do kategorii C Z ( $II$ losowanie). Na tym etapie są cztery kule białe i pięć czarnych.
- Nazwa kategorii: B ( $III$ losowanie).
- Nazwa kategorii: C Z ( $III$ losowanie).
Elementy należące do kategorii C Z ( $I$ losowanie). Na tym etapie jest pięć kul białych i pięć czarnych.
- Nazwa kategorii: B ( $II$ losowanie).
- Nazwa kategorii: C Z ( $II$ losowanie).
Elementy należące do kategorii B ( $II$ losowanie). Na tym etapie są cztery kule białe i pięć czarnych.
- Nazwa kategorii: B ( $III$ losowanie).
- Nazwa kategorii: C Z ( $III$ losowanie).
Elementy należące do kategorii C Z ( $II$ losowanie). Na tym etapie jest pięć kul białych i cztery czarne.
- Nazwa kategorii: B ( $III$ losowanie).
- Nazwa kategorii: C Z ( $III$ losowanie).

Liczba wszystkich wyników losowania dokładnie jednej kuli białej wynosi: $5 \cdot 6 \cdot 5 + 6 \cdot 5 \cdot 5 + 6 \cdot 5 \cdot 5 = 150 + 150 + 150 = 450$ .

Koniec prezentacji.

Polecenie 1

W pojemniku znajduje się $6$ kul czerwonych i $4$ kule zielone. Losujemy kolejno dwie kule bez zwracania. Oblicz, ile jest wszystkich możliwości wylosowania dwóch kul tego samego koloru.

RJBszBGuiEEvh

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Jeżeli wylosujemy dwie kule tego samego koloru, to liczba możliwych wyborów wynosi:

dla dwóch kul czerwonych: $6 \cdot 5 = 30$ ,
dla dwóch kul zielonych: $4 \cdot 3 = 12$ .

Wobec tego, liczba wszystkich możliwych wyborów dwóch kul tego samego koloru wynosi:

$6 \cdot 5 + 4 \cdot 3 = 30 + 12 = 42$ .

Polecenie 2

W pojemniku znajduje się $7$ kul czerwonych i $3$ kule zielone. Losujemy kolejno dwie kule bez zwracania. Oblicz, ile jest wszystkich możliwych wyborów dwóch kul o różnych kolorach.

RDqG4yDJmkQzf

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Jeżeli wylosujemy dwie kule różnego koloru, to liczba możliwych wyborów wynosi:

dla pierwszej kuli czerwonej, a drugiej zielonej: $7 \cdot 3 = 21$ ,
dla pierwszej kuli zielonej, a drugiej czerwonej: $3 \cdot 7 = 21$ .

Wobec tego, liczba wszystkich możliwych wyborów dwóch kul o różnych kolorach wynosi:

$7 \cdot 3 + 3 \cdot 7 = 21 + 21 = 42$ .

Polecenie 3

Wzorując się na zadaniu rozwiązanym w Prezentacji, oblicz ile jest wszystkich liczb trzycyfrowych o niepowtarzających się cyfrach, większych od $199$ .

RFTReo3WnVBRO

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Liczby trzycyfrowe większe od $199$ , to: $200, 201, 202, . . . ., 999 .$

Cyfra setek – $8$ możliwości,

cyfra dziesiątek – $9$ możliwości,

cyfra jedności – $8$ możliwości.

$8 \cdot 9 \cdot 8 = 576$ .

Jest $576$ takich liczb.

Zestaw ćwiczeń interaktywnych

RMtKa0tqDjw2y

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

R1WcYiMjcdhVW

Ćwiczenie 2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1aVK7DYkuOx4

Ćwiczenie 3

Tworzymy liczby wielocyfrowe o różnych cyfrach ze zbioru

\{1, 2, 3, 5, 7, 8, 9\}

. Połącz w pary liczbę cyfr z liczbą różnych możliwości jej otrzymania. liczba dwucyfrowa Możliwe odpowiedzi: 1.

5040

, 2.

840

, 3.

210

, 4.

42

liczba czterocyfrowa Możliwe odpowiedzi: 1.

5040

, 2.

840

, 3.

210

, 4.

42

liczba sześciocyfrowa Możliwe odpowiedzi: 1.

5040

, 2.

840

, 3.

210

, 4.

42

liczba trzycyfrowa Możliwe odpowiedzi: 1.

5040

, 2.

840

, 3.

210

, 4.

42

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RnAo7Cnsz7lYB

Ćwiczenie 4

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

R1VYZDzD5OvvE

Ćwiczenie 5

Do windy zatrzymującej się na

n

piętrach wsiadło

k

osób. Pogrupuj elementy zgodnie z podanym opisem. Jeżeli

n = 9

, to liczba sposobów, na które osoby te mogą opuścić windę, przy założeniu, że każdy wysiada na innym piętrze wynosi: Możliwe odpowiedzi: 1. dla

k = 3

wynosi

720

, 2. dla

k = 4

wynosi

5040

, 3. dla

k = 5

wynosi

30240

, 4. dla

k = 4

wynosi

3024

, 5. dla

k = 5

wynosi

15120

, 6. dla

k = 3

wynosi

504

Jeżeli

n = 11

, to liczba sposobów, na które osoby te mogą opuścić windę, przy założeniu, że każdy wysiada na innym piętrze i nikt nie wysiada na ostatnim piętrze wynosi: Możliwe odpowiedzi: 1. dla

k = 3

wynosi

720

, 2. dla

k = 4

wynosi

5040

, 3. dla

k = 5

wynosi

30240

, 4. dla

k = 4

wynosi

3024

, 5. dla

k = 5

wynosi

15120

, 6. dla

k = 3

wynosi

504

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

R6rnyqa1a2LdI

Ćwiczenie 6

Wstaw w tekst odpowiednie liczby.

4

- osobową kolejkę wybierając ludzi z

13

- osobowej grupy możemy ustawić na 1.

17160

, 2.

100000

, 3.

1320

, 4.

1728

, 5.

28561

, 6.

30240

sposobów.

5

- osobową kolejkę wybierając ludzi z

10

- osobowej grupy możemy ustawić na 1.

17160

, 2.

100000

, 3.

1320

, 4.

1728

, 5.

28561

, 6.

30240

sposobów.

3

- osobową kolejkę wybierając ludzi z

12

- osobowej grupy możemy ustawić na 1.

17160

, 2.

100000

, 3.

1320

, 4.

1728

, 5.

28561

, 6.

30240

sposobów.

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 7

Oblicz, ile jest wszystkich:

ośmiocyfrowych numerów telefonicznych, rozpoczynających się od $32$ , w których żadna cyfra się nie powtarza,
dziewięciocyfrowych numerów telefonicznych, rozpoczynających się od $3125$ , w których żadna cyfra się nie powtarza.

Rttc1nhAidXZr

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Jeżeli numer telefonu rozpoczyna się od cyfr $3$ oraz $2$ i żadna cyfra się nie powtarza, to mamy do dyspozycji cyfry $0, 1, 4, 5, 6, 7, 8, 9$ .

Zauważmy, że pierwsza i druga cyfra numeru telefonicznego są zajęte, zatem mamy do dyspozycji $8$ cyfr, które musimy rozmieścić na pozostałych $6$ miejscach tak, aby cyfry się nie powtarzały.
Zatem liczba możliwych wyników omawianego doświadczenia losowego wynosi:
$8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 = 20160$ .
Zauważmy, że pierwsze cztery cyfry numeru telefonicznego są zajęte, zatem mamy do dyspozycji $6$ cyfr, które musimy rozmieścić na pozostałych $5$ miejscach tak, aby cyfry się nie powtarzały.
Zatem liczba możliwych wyników omawianego doświadczenia losowego wynosi:
$6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 = 720$ .

Ćwiczenie 8

W pojemniku znajdują się ponumerowane kartki z cyframi od $1$ do $9$ . Losujemy bez zwracania kolejno trzy kartki i z otrzymanych cyfr układamy liczbę tak, że pierwsza wylosowana cyfra jest cyfrą setek, druga cyfrą dziesiątek, trzecia cyfrą jedności. Oblicz, ile jest możliwych wyników doświadczenia losowego polegającego na otrzymaniu liczby, która jest podzielna przez $5$ .

RwExk8vMn8nK4

Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.

Liczba jest podzielna przez $5$ , gdy cyfrą jej jedności jest $0$ lub $5$ .

Zauważmy, że liczba wszystkich możliwych wyników doświadczenia losowego wynosi:

$9 \cdot 8 \cdot 7 = 504$ .

Wypiszmy liczby, które spełniają warunki zadania, gdy cyfrą setek tej liczby jest:

$1$ : $125$ , $135$ , $145$ , $165$ , $175$ , $185$ , $195$
$2$ : $215$ , $235$ , $245$ , $265$ , $275$ , $285$ , $295$ ,
$3$ : $315$ , $325$ , $345$ , $365$ , $375$ , $385$ , $395$ ,
$4$ : $415$ , $425$ , $435$ , $465$ , $475$ , $485$ , $495$ ,
$6$ : $615$ , $625$ , $635$ , $645$ , $675$ , $685$ , $695$ ,
$7$ : $715$ , $725$ , $735$ , $745$ , $765$ , $785$ , $795$ ,
$8$ : $815$ , $825$ , $835$ , $845$ , $865$ , $875$ , $895$ ,
$9$ : $915$ , $925$ , $935$ , $945$ , $965$ , $975$ , $985$ .

Zatem liczba wszystkich wyników omawianego doświadczenia losowego, spełniających warunki zadania wynosi:

$8 \cdot 7 \cdot 1 = 56$ .

Słownik

kombinatoryka

dziedzina matematyki zajmująca się zbiorami, wyznaczaniem liczby elementów zbiorów, oraz odwzorowaniami jednego zbioru w drugi zgodnie z wyznaczonymi kryteriami

doświadczenie losowe

procedura, którą można powtarzać wielokrotnie, mająca określony zbiór wyników, których nie da się przewidzieć

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

2. Losowanie ze zwracaniem

Kombinatoryka