Rozwiązywanie problemów z fizyki jest niczym innym jak liczbowym opisem zjawisk otaczającego nas świata. Wyznaczamy konkretne wartości wielkości fizycznych mających wpływ na nasze życie – temperatury, ciśnienia, prędkości, przyspieszenia i wielu innych, których nie sposób w tym miejscu przytoczyć. Dzięki obliczeniom możemy przewidzieć, jak wysoko wzniesie się samolot lub jak głęboko zanurzy się łódź podwodna. Obliczenia i rozwiązywanie problemów są podstawą funkcjonowania cywilizacji technicznej stworzonej przez człowieka. Rozwiązujmy więc zadania…

R115muKEeWmrt1

Już potrafisz

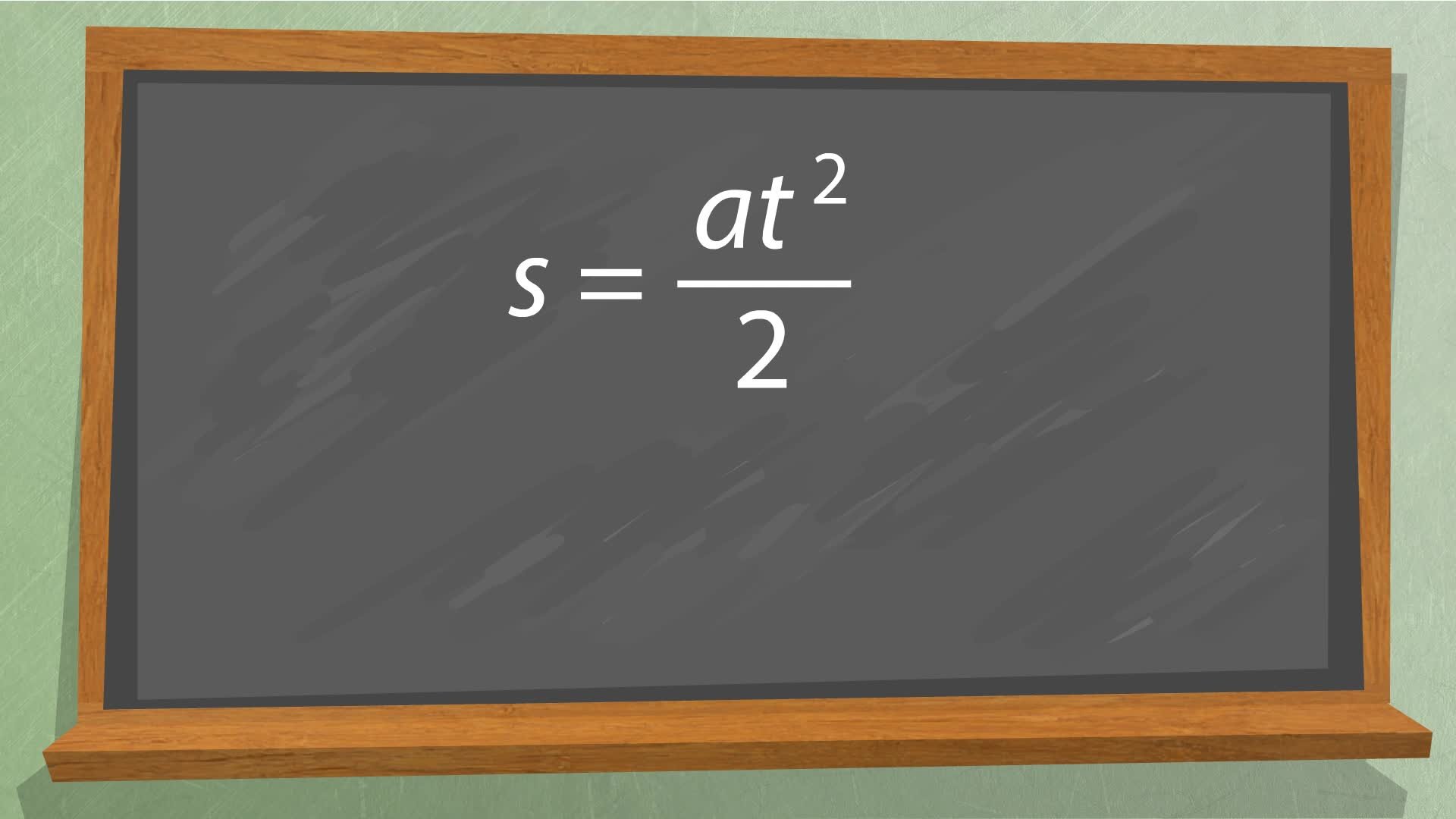
obliczać przyspieszenie, prędkość i drogę w ruchu jednostajnie przyspieszonym prostoliniowym;
tworzyć wykresy zależności: przyspieszenia od czasu a(t), prędkości od czasu v(t) i drogi od czasu s(t) w ruchu jednostajnie przyspieszonym prostoliniowym.

Nauczysz się

rozwiązywać zadania dotyczące ruchu jednostajnie przyspieszonego prostoliniowego.

i4nhNI6Tsq_d5e129

1. Wykorzystanie wzoru na drogę i przyspieszenie

Czasem, rozwiązując zadanie, możemy po prostu wstawić w miejsce ogólnych symboli odpowiadające im wartości. Na przykład obliczając drogę przebytą ruchem jednostajnie przyspieszonym przez ciało poruszające się przez 10 sekund z przyspieszeniem a = 2 m/sIndeks górny 2, korzystamy z odpowiedniej zależności:
$s = \frac{a \cdot t^{2}}{2} = \frac{2 \frac{m}{s^{2}} \cdot {(10 s)}^{2}}{2} = \frac{2 \frac{m}{s^{2}} \cdot 100 s^{2}}{2} = \frac{200 m}{2} = 100 m$
Jak powinniśmy postąpić w przypadku, gdy nie znamy przyspieszenia? Polecenie zawarte w tym zadaniu brzmi: oblicz drogę przebytą przez ciało w ciągu 10 sekund, jeżeli w tym czasie wartość jego prędkości wzrosła od zera do 20 m/s?
Jeśli zapiszemy zależność drogi od czasu tak jak poprzednio: $s = \frac{a \cdot t^{2}}{2}$ , to widzimy, że nieznana jest nam wartość przyspieszenia ciała. Czy jednak na pewno? Przecież znamy definicję przyspieszenia: $a = \frac{∆ v}{∆ t}$ . Czytając jeszcze raz treść zadania, dochodzimy do wniosku, że znamy zmianę wartości prędkości (równą wartości prędkości końcowej, ponieważ prędkość początkowa była równa zero) i czas, w jakim ta zmiana nastąpiła. Obliczamy:
$a = \frac{∆ v}{t} = \frac{20 \frac{m}{s} - 0}{10 s} = \frac{20 \frac{m}{s}}{10 s} = 2 \frac{m}{s^{2}}$ ,
a następnie wykorzystujemy obliczoną wartość przyspieszenia do obliczenia przebytej drogi. Warto podkreślić, że aby obliczyć zmianę wartości prędkości, odejmujemy (zawsze!) od wartości końcowej wartość początkową.

RIndbQk8pWenk1

Jak wyznaczyć drogę i przyspieszenie w ruchu jednostajnie przyspieszonym

Film dostępny na portalu epodreczniki.pl

Jak wyznaczyć drogę i przyspieszenie w ruchu jednostajnie przyspieszonym

W przypadku prostoliniowego ruchu jednostajnie przyspieszonego, w którym ciało nie miało prędkości początkowej, to znaczy spoczywało w chwili t = 0, posługujemy się dwoma podstawowymi wzorami. Znajomość tych wzorów jest wystarczająca do rozwiązywania problemów związanych z ruchem jednostajnie przyspieszonym prostoliniowym. Przykładowo, gdy chcemy obliczyć przyspieszenie. znając przebytą drogę, np. przez rowerzystę, który poruszał się przez pewien czas t, wystarczy przekształcić wzór na drogę: Mnożymy wzór obustronnie przez 2. Następnie dzielimy obustronnie przez t2 i w rezultacie otrzymujemy: Zamieniamy równanie stronami, by otrzymać bardziej elegancką postać: I mamy gotowy wzór na wartość przyspieszenia. Możemy jeszcze dodatkowo sprawdzić, czy otrzymamy prawidłowe jednostki. W miejsce symboli wstawiamy odpowiednie jednostki miary i dostajemy m/s2.

Polecenie 1

Samochód wjeżdżający na drogę szybkiego ruchu musi uzyskać prędkość 90 km/h. Przyjmując, że prędkość początkowa była równa zero, a długość pasa rozbiegowego wynosi 150 m, oblicz minimalne przyspieszenie, z jakim musi poruszać się samochód.

Wskazówka

Pamiętaj o przeliczeniu jednostek na jednostki podstawowe układu SI.

Polecenie 2

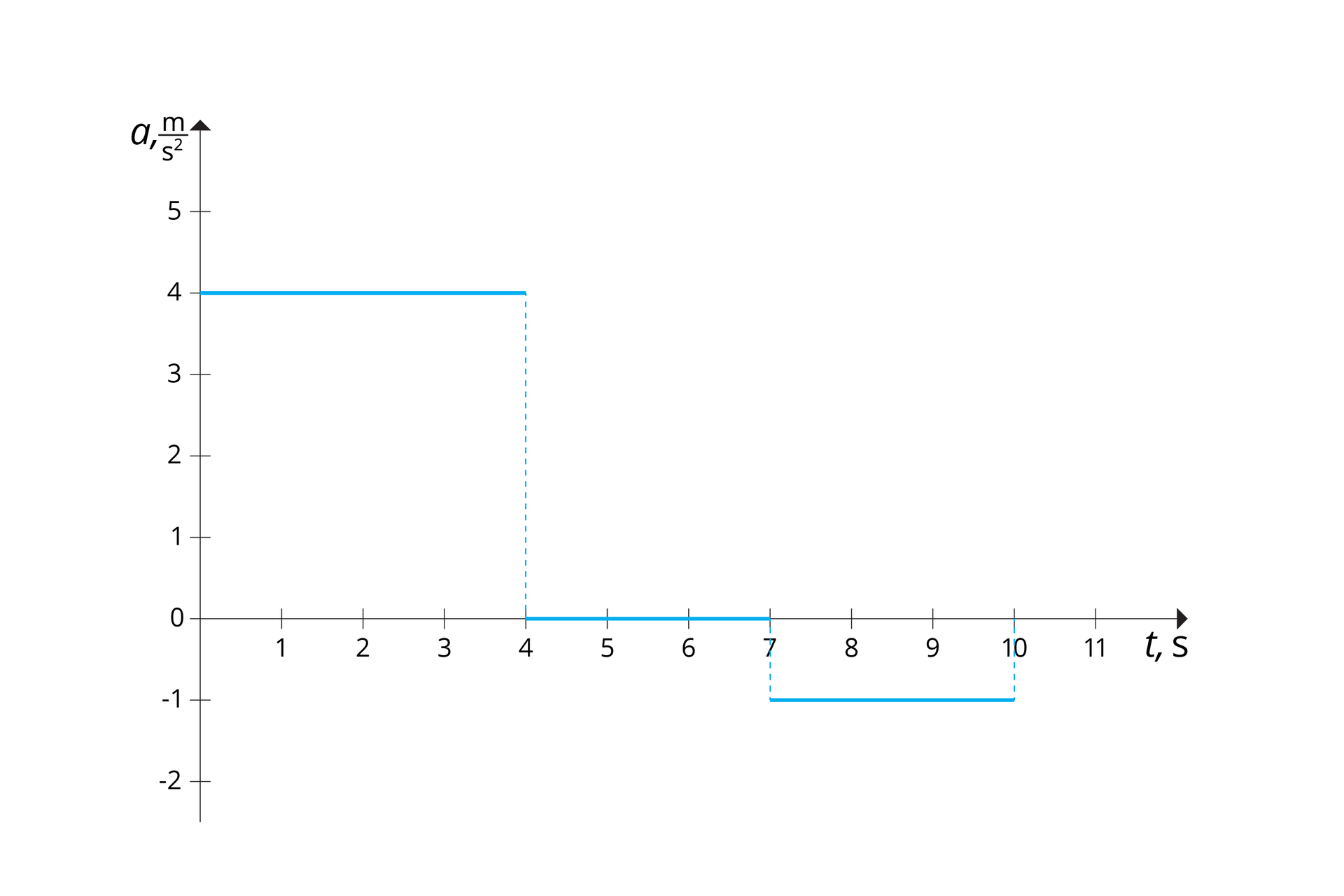
*Na podstawie wykresu zależności przyspieszenia od czasu nazwij rodzaje ruchów, którymi poruszało się ciało, oraz oblicz odpowiadające im prędkości początkowe i końcowe.

R15bdSHjHRPJ21

Ilustracja przedstawia wykres zależności przyspieszenia od czasu. Tło białe. Oś odciętych od 0 do 11, co 1, opisana „t, s”. Oś rzędnych od -2 do 5, co 1, opisana „a, m/s do kwadratu”. Wykres składa się z trzech niebieskich odcinków. Pierwszy: początek (0, 4) i koniec (4, 4). Drugi: początek (4, 0) i koniec (7, 0). Trzeci: początek (-1, 7) i koniec (10, -1).

i4nhNI6Tsq_d5e221

2. Obliczanie czasu trwania ruchu przyspieszonego

Znając przebytą drogę przez ciało i przyspieszenie, z jakim się poruszało, jesteśmy w stanie obliczyć czas trwania ruchu. Zobacz, jak można to zrobić.

REuiMkPHYCf0w1

Jak obliczyć czas trwania ruchu w ruchu jednostajnie przyspieszonym?

Film dostępny na portalu epodreczniki.pl

Jak obliczyć czas trwania ruchu w ruchu jednostajnie przyspieszonym?

Na tablicy pojawiają się wzory oraz działania na nich, o kótych mówi lektor. Czyli: s=at^2/2 pomnożone obustronnie przez 2 co daje 2*s=at^2 podzielone obustronnie przez a. W rezultacie otrzymujemy 2s/a=t^2. Następnie obustronnie pierwiastkujemy to równanie co daje nam t=pierwiastek z 2s/a.

Polecenie 3

Oblicz czas potrzebny do tego, aby samochód mający podczas ruchu stałe przyspieszenie 3 m/sIndeks górny 2 przebył drogę 1,5 km.

Polecenie 4

Jeden z uczniów ułożył następujące zadanie: pociąg wyruszył ze stacji i przejechał 80 km ze stałym przyspieszeniem wynoszącym $1 \frac{m}{s^{2}}$ . Na podstawie tych informacji oblicz czas podróży i wartość prędkości końcowej. Przeanalizuj wyniki i treść zadania, a potem napisz, dlaczego zadanie z takimi założeniami nie ma odzwierciedlenia w rzeczywistości.

Polecenie 5

Kierowca Formuły 1 zauważył zakręt i rozpoczął hamowanie przy szybkości $288 \frac{km}{h}$ . Przed wejściem w zakręt, po przebyciu odległości s = 120 m, licznik prędkościomierza bolidu wskazywał $144 \frac{km}{h}$ . Zakładając, że ruch bolidu był ruchem jednostajnie opóźnionym, oblicz:

przyspieszenie bolidu;
czas, w którym bolid zmniejszył swoją prędkość.

i4nhNI6Tsq_d5e290

3. Jak obliczyć drogę, nie znając przyspieszenia?

Czasami w przypadku obliczeń znamy jedynie prędkość końcową ciała i czas trwania ruchu. Jak wobec tego obliczyć drogę? Sprawdźmy to wspólnie.

RRBWBe2Ho0ViK1

Jak obliczyć drogę, nie znając przyspieszenia w ruchu jednostajnie przyspieszonym?

Film dostępny na portalu epodreczniki.pl

Jak obliczyć drogę, nie znając przyspieszenia w ruchu jednostajnie przyspieszonym?

Zdarzają się przypadki, gdy chcemy obliczyć prędkość końcową ciała lub nie znamy przyspieszenia, a znamy właśnie prędkość końcową. Wówczas możemy podstawić wzór na przyspieszenie do wzoru na drogę. Tym sposobem bez problemu jesteśmy w stanie obliczyć: drogę, znając tylko wartość prędkości końcowej i czas trwania ruchu; wartość prędkości końcowej, znając przebytą drogę oraz czas trwania ruchu; czas trwania ruchu, znając drogę i prędkość końcową.

Polecenie 6

Oblicz, jaką prędkość w ciągu 10 s osiągnie pojazd poruszający się ruchem jednostajnie przyspieszonym prostoliniowym po przebyciu drogi równej 200 m?

Wskazówka: oblicz najpierw przyspieszenie pojazdu (znasz czas i drogę).

Polecenie 7

Samochód ruszył ze skrzyżowania i ruchem jednostajnie przyspieszonym przebył drogę 1000 m w czasie 100 s. Oblicz przyspieszenie pojazdu i wyraź jego prędkość końcową w $\frac{km}{h}$ .
Sporządź wykresy zależności prędkości od czasu v(t), przyspieszenia od czasu a(t) i drogi od czasu s(t) dla tego ruchu.

i4nhNI6Tsq_d5e350

Podsumowanie

Wzory wykorzystywane do rozwiązywania zadań dotyczących ruchu jednostajnie przyspieszonego prostoliniowego
Wzór	Opis
$s = \frac{a t^{2}}{2}$	Droga przebyta przez ciało rozpoczynające ruch ze stanu spoczynku (prędkość początkowa $v_{0} = 0 \frac{m}{s}$ )
$a = \frac{v_{k} - v_{0}}{t}$	Przyspieszenie
$v_{k} = a \cdot t$ $v_{k} = \frac{2 \cdot s}{t}$	Prędkość końcowa ( $v_{0} = 0 \frac{m}{s}$ ) w ruchu przyspieszonym
$t = \sqrt{\frac{2 \cdot s}{a}}$ $t = \frac{v_{k}}{a}$	Czas przebycia danej drogi lub czas osiągnięcia danej prędkości (jeśli znane jest przyspieszenie). Prędkość początkowa $v_{0} = 0 \frac{m}{s}$ .

Praca domowa

Polecenie 8.1

Uzupełnij tabelę dotyczącą prędkości i przebytej drogi w ruchu jednostajnie przyspieszonym prostoliniowym.

Praca domowa
Czas t [s]	1	4	10	20
Prędkość $v [\frac{m}{s}]$	4	......	......	.....
Droga $s [m]$	2	32	......	......

Polecenie 8.2

Oblicz końcową prędkość samochodu, który ruszył z miejsca i w czasie 20 s przebył drogę równą 100 m.

Polecenie 8.3

Pocisk przeciwpancerny porusza się w lufie armaty z przyspieszeniem $a = 8 \cdot 10^{4} \frac{m}{s^{2}}$ przez czas 0,01 s. Oblicz długość lufy i prędkość pocisku na końcu lufy.

i4nhNI6Tsq_d5e411

Zadania

Ćwiczenie 1

R1RycJAkRyIHh1

Który zestaw zależności opisujących ruch jednostajnie przyspieszony zawiera tylko prawdziwe zależności?

$t = \sqrt{\frac{2 \cdot s}{a}}; s = \frac{v_{k} \cdot t}{2}; s = \frac{a \cdot t^{2}}{2}$
$s = \frac{v_{k}}{t}; v_{k} = s \cdot t; t = \frac{v}{s}$
$v_{k} = \frac{s}{t}; s = v_{k} \cdot t; s = \frac{v_{k} \cdot t}{2}$

Ćwiczenie 2

R1cWg3Q6xIK9D1

Uzupełnij puste miejsce.

Samochód, który w czasie 10 s osiągnął wartość prędkości równą 18 m/s przejechał drogę równą ............ m.

Rysowanie i analiza wykresów zależności drogi i prędkości od czasu w ruchu jednostajnie przyspieszonym prostoliniowym

Ruchy jednostajny prostoliniowy i jednostajnie przyspieszony prostoliniowy w zadaniach

Rozwiązywanie zadań dotyczących ruchu jednostajnie przyspieszonego prostoliniowego

1. Wykorzystanie wzoru na drogę i przyspieszenie

2. Obliczanie czasu trwania ruchu przyspieszonego

3. Jak obliczyć drogę, nie znając przyspieszenia?

Podsumowanie

Zadania