Film dostępny pod adresem /preview/resource/R1PVSTBA6DSRM

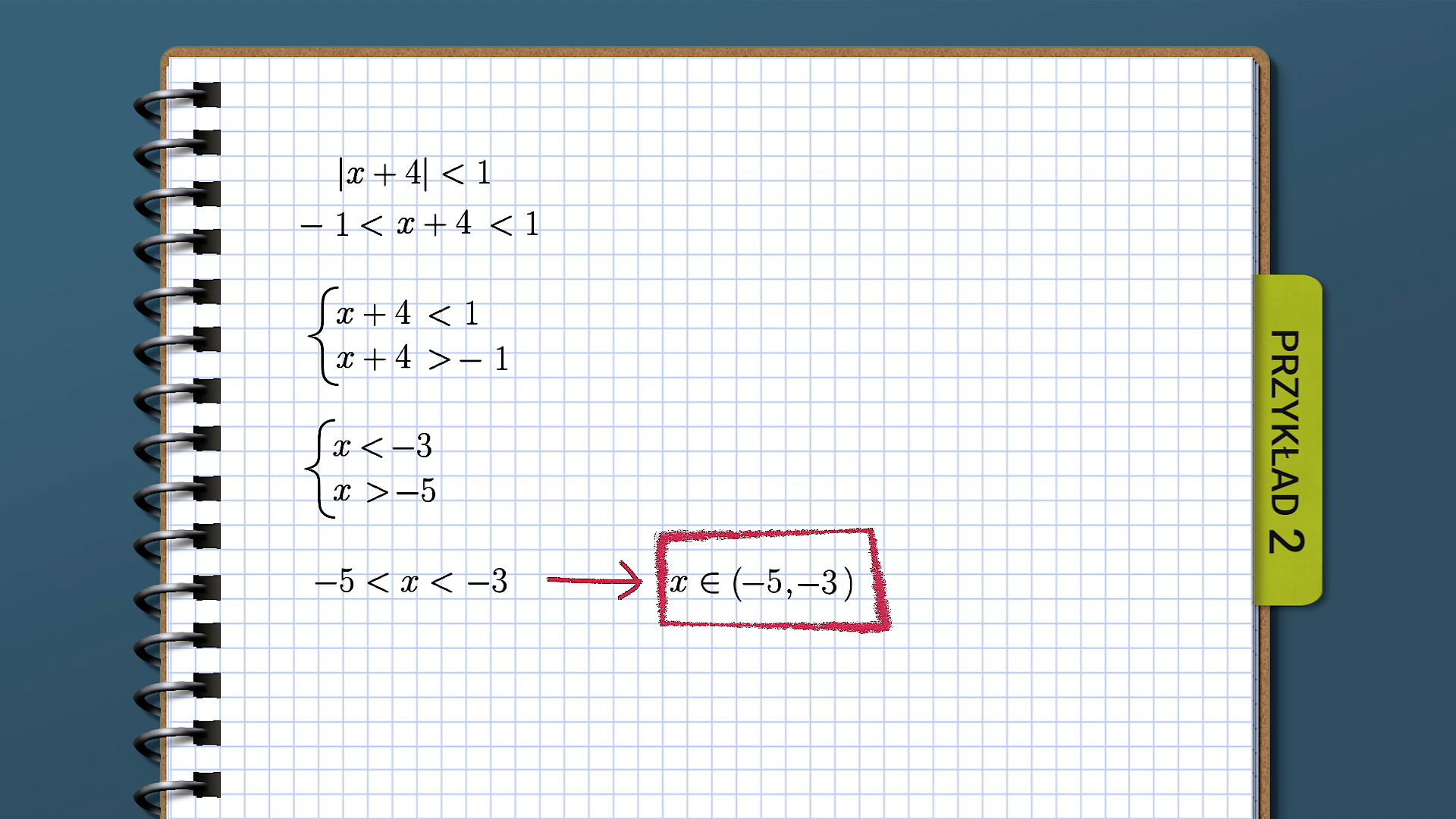
Przykład pierwszy: X minus pięć jest mniejsze niż początek ułamka jeden mianownik dwa koniec ułamka razy X plus cztery jest mniejsze niż trzy plus sześć X. Zapisujemy to w postaci układu dwóch nierówności: X minus pięć jest większe niż początek ułamka jeden mianownik dwa koniec ułamka razy X plus cztery oraz początek ułamka jeden mianownik dwa koniec ułamka razy X plus cztery jest mniejsze niż trzy plus sześć X. Przekształcamy każdą z nierówności układu. Pierwsza nierówność przyjmuje postać X minus początek ułamka jeden mianownik dwa koniec ułamka razy X jest mniejsze niż cztery plus pięć. Druga nierówność początek ułamka jeden mianownik dwa koniec ułamka razy X minus sześć X jest mniejsze niż trzy minus cztery. Ponownie przekształcamy każdą z nierówności układu. Pierwsza nierówność przyjmuje postać: początek ułamka jeden mianownik dwa koniec ułamka razy X jest mniejsze niż dziewięć oraz druga nierówność minus pięć i jedna druga razy X jest mniejsze niż minus jeden. Następnie pierwszą nierówność z układu mnożymy przez dwa, a drugą przez minus dwie jedenaste. Wychodzi nam: X jest mniejsze niż osiemnaście oraz X jest większe niż dwie jedenaste. Przykład drugi. Wartość bezwzględna X plus cztery jest mniejsza niż jeden. Zapisujemy nierówność równoważnie. Minus jeden jest mniejsze niż X plus cztery jest mniejsze niż jeden. Zapisujemy w postaci koniunkcji dwóch nierówności: X plus cztery jest mniejsze niż jeden oraz X plus cztery jest większe niż minus jeden. Przekształcając otrzymujemy X jest mniejsze niż minus trzy oraz X jest większe niż minus pięć. Wychodzi nam, że rozwiązaniem jest każda liczba rzeczywista która jest większa niż minus pięć oraz mniejsza niż minus trzy.