Aplet
Polecenie 1
Uruchom aplet, a następnie odczytaj z wykresu funkcji potęgowej następujące własności: dziedzinę, zbiór wartości, miejsca zerowe (o ile istnieją) oraz przedziały monotoniczności.
Zapoznaj się z apletem.
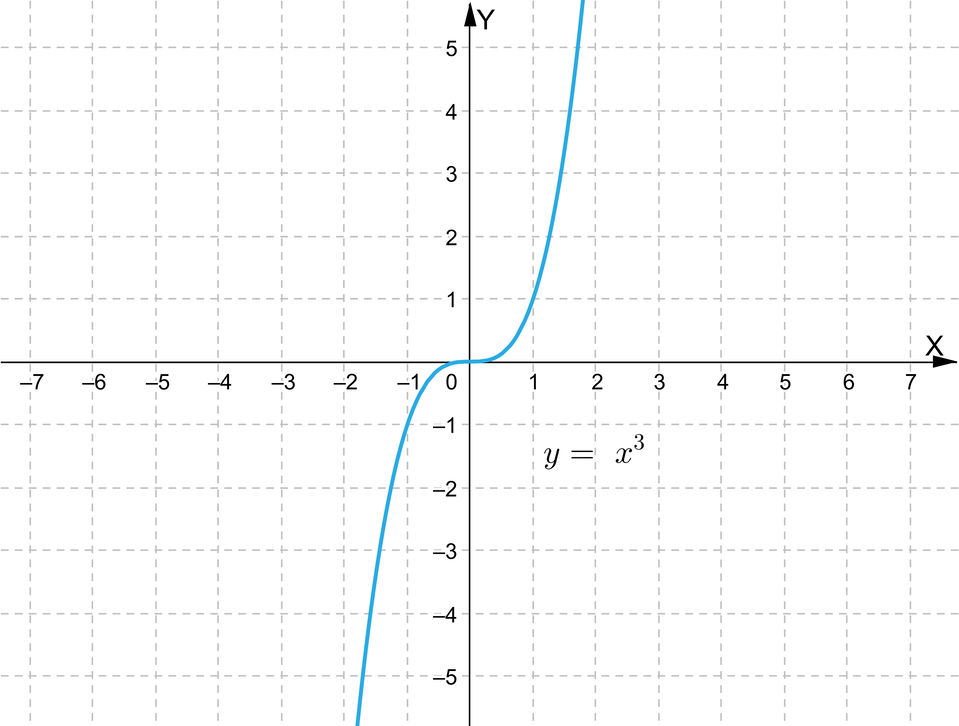
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DcHsoLhCH
Polecenie 2
Na rysunku przedstawiono wykres funkcji potęgowej określonej wzorem .
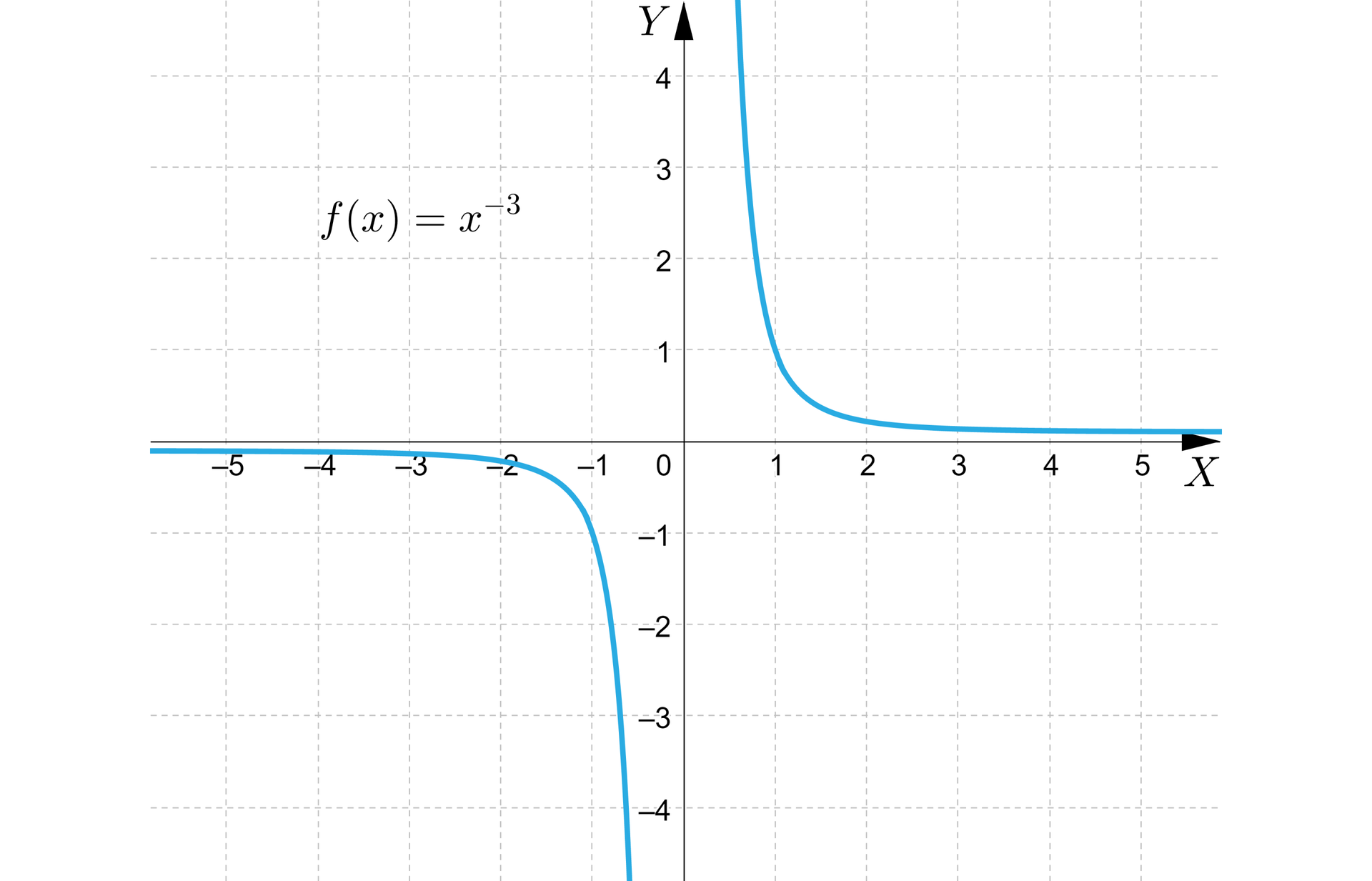
Odczytaj z wykresu:
a) dziedzinę i zbiór wartości funkcji,
b) przedziały monotoniczności funkcji,
c) miejsca zerowe funkcji (o ile istnieją).
Oblicz wartość tej funkcji dla argumentów oraz .