W materiale przypomnimy definicję funkcji potęgowej oraz sklasyfikujemy funkcje potęgowefunkcja potęgowafunkcje potęgowe na podstawie ich wykresów oraz własności.

W zależności od wartości wykładnika $m$ wyróżnia się następujące rodzaje funkcji potęgowych:

1. dla $m=0$

   Funkcja jest określona wzorem $f\left(x\right)=x^0=1$.

   Dziedziną tej funkcji jest zbiór $\mathrm{ℝ}\setminus \left\{0\right\}$, a zbiorem wartości $\left\{1\right\}$.

   Wykres tej funkcji przedstawia się następująco:

   R18YevnoUdy6t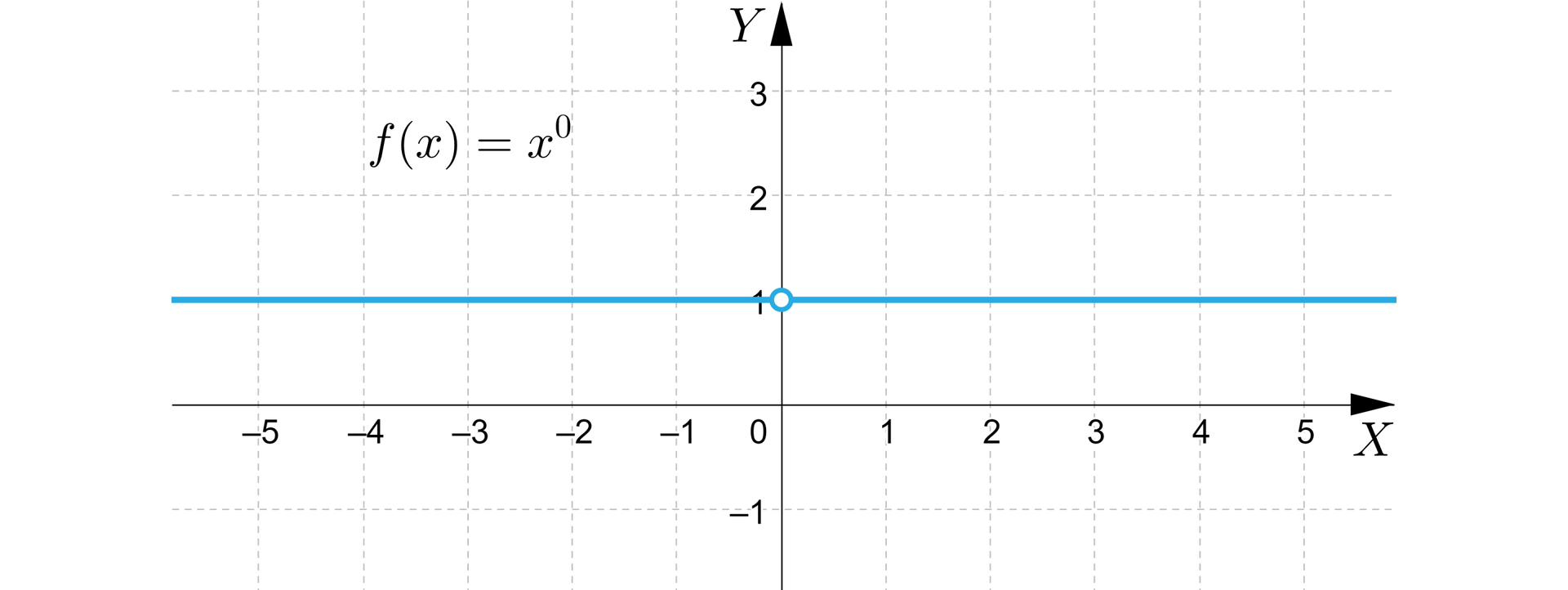

   Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 1 do trzy. W układzie zaznaczono wykres funkcji o równaniu $f\left(x\right)=x^0$. Ma ona kształt poziomej prostej przecinającej oś y w niezamalowanym punkcie o współrzędnych nawias zero średnik jeden zamknięcie nawiasu.

   

   Własności funkcji, której wykres przedstawiono na rysunku:

   • funkcja jest stała w przedziale $\left(-\infty ,0\right)$ oraz $\left(0,\infty \right)$,

   • funkcja nie ma miejsc zerowych,

   • funkcja nie jest różnowartościowa.

2. dla $m=1$

   Funkcja jest określona wzorem $f\left(x\right)=x^1=x$.

   Dziedziną oraz zbiorem wartości tej funkcji jest zbiór liczb $\mathrm{ℝ}$.

   Wykres tej funkcji przedstawia się następująco:

   RglXN1mzjz7oA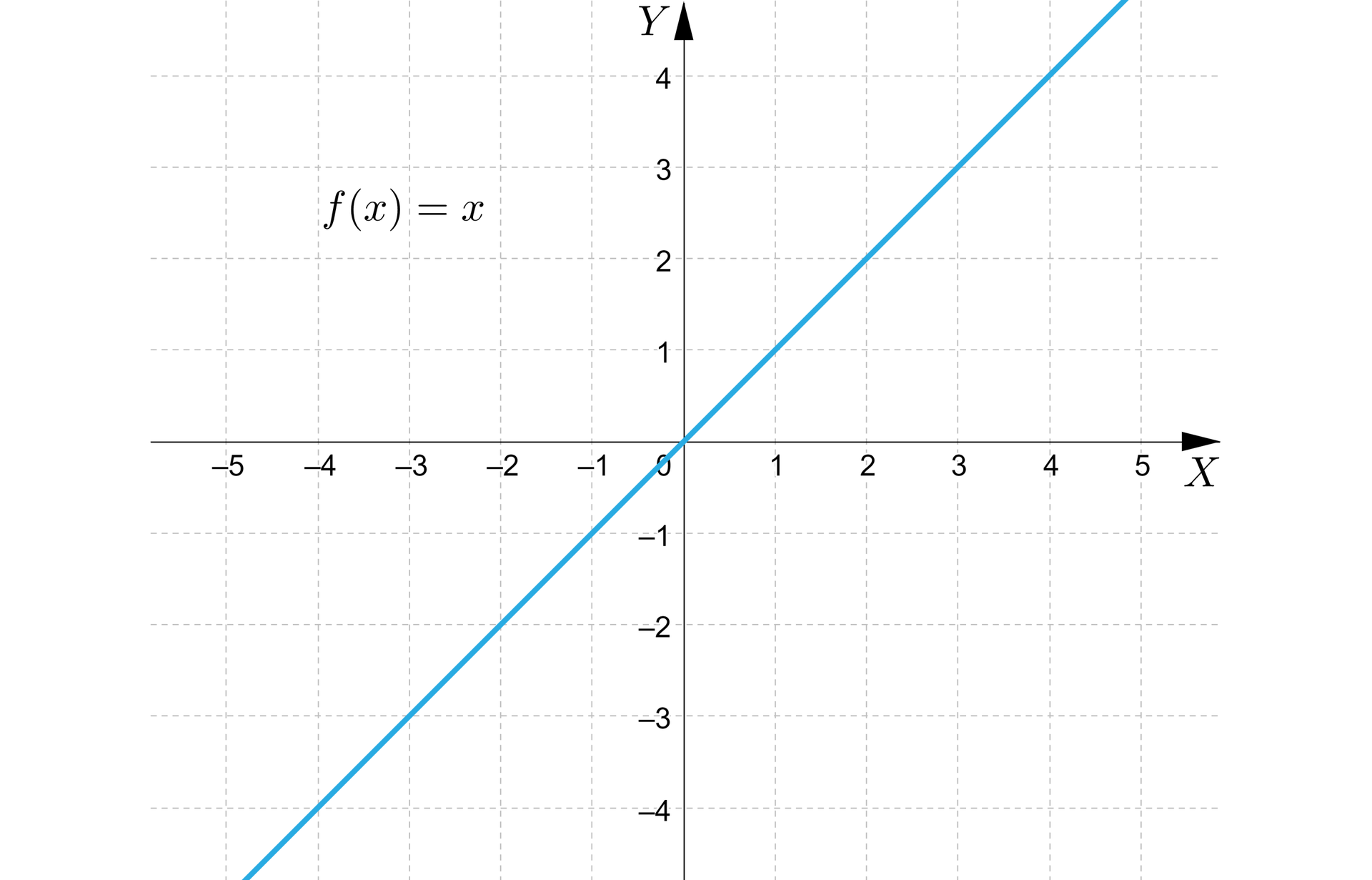

   Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 4 do cztery. W układzie zaznaczono wykres funkcji o równaniu $f\left(x\right)=x$. Ma ona kształt ukośnej prostej która przechodzi przez punkty nawias minus dwa średnik minus dwa zamknięcie nawiasu i nawias trzy średnik trzy zamknięcie nawiasu.

   

   Własności funkcji, której wykres przedstawiono na rysunku:

   • funkcja jest rosnąca w całej swojej dziedzinie,

   • funkcja jest różnowartościowa,

   • miejscem zerowym funkcji jest liczba $0$,

   • funkcja nie ma wartości największej oraz wartości najmniejszej.

3. dla $m>1$, gdy $m$ jest liczbą nieparzystą

   Funkcja jest określona wzorem $f\left(x\right)=x^{2k+1}$, gdzie $m=2k+1$ oraz $k\in {\mathrm{\mathbb{N}}}_{+}$.

   Dziedziną oraz zbiorem wartości tej funkcji jest zbiór liczb $\mathrm{ℝ}$.

   Na przykład wykres funkcji określonej wzorem $f\left(x\right)=x^3$ przedstawia się następująco:

   R1uC9HVLoZ0xz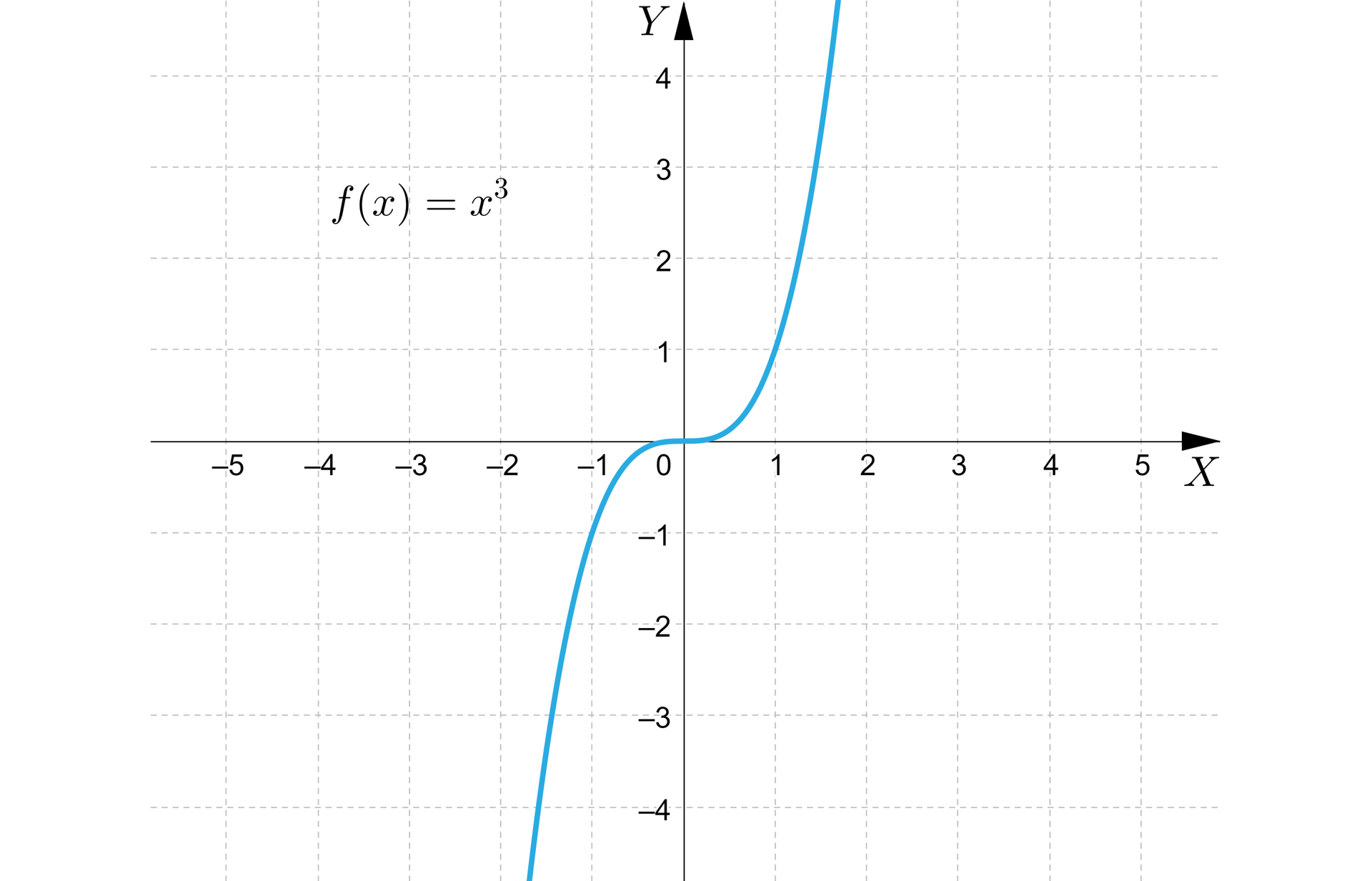

   Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 4 do cztery. W układzie zaznaczono wykres funkcji o równaniu $f\left(x\right)=x^3$. Pojawia się on w trzeciej ćwiartce układu i biegnie delikatnie po łuku przez punkt nawias minus jeden średnik minus jeden zamknięcie nawiasu, następnie występuje wypłaszczenie na osi x i funkcja przechodzi przez środek układu współrzędnych następnie biegnie po łuku przez punkt nawias jeden średnik jeden zamknięcie nawiasu i wychodzi poza płaszczyznę układu w pierwszej ćwiartce.

   

   Własności funkcji, której wykres przedstawiono na rysunku:

   • funkcja jest rosnąca w całej swojej dziedzinie,

   • funkcja jest różnowartościowa,

   • miejscem zerowym funkcji jest liczba $0$,

   • funkcja nie ma wartości największej oraz wartości najmniejszej.

4. dla $m>1$, gdy $m$ jest liczbą parzystą

   Funkcja jest określona wzorem $f\left(x\right)=x^{2k}$, gdzie $m=2k$ oraz $k\in {\mathrm{\mathbb{N}}}_{+}$.

   Dziedziną tej funkcji jest zbiór liczb $\mathrm{ℝ}$, a zbiorem wartości ${\mathrm{ℝ}}_{+}\cup \left\{0\right\}$.

   Na przykład wykres funkcji określonej wzorem $f\left(x\right)=x^4$ przedstawia się następująco:

   R18Z0jyOdOmaT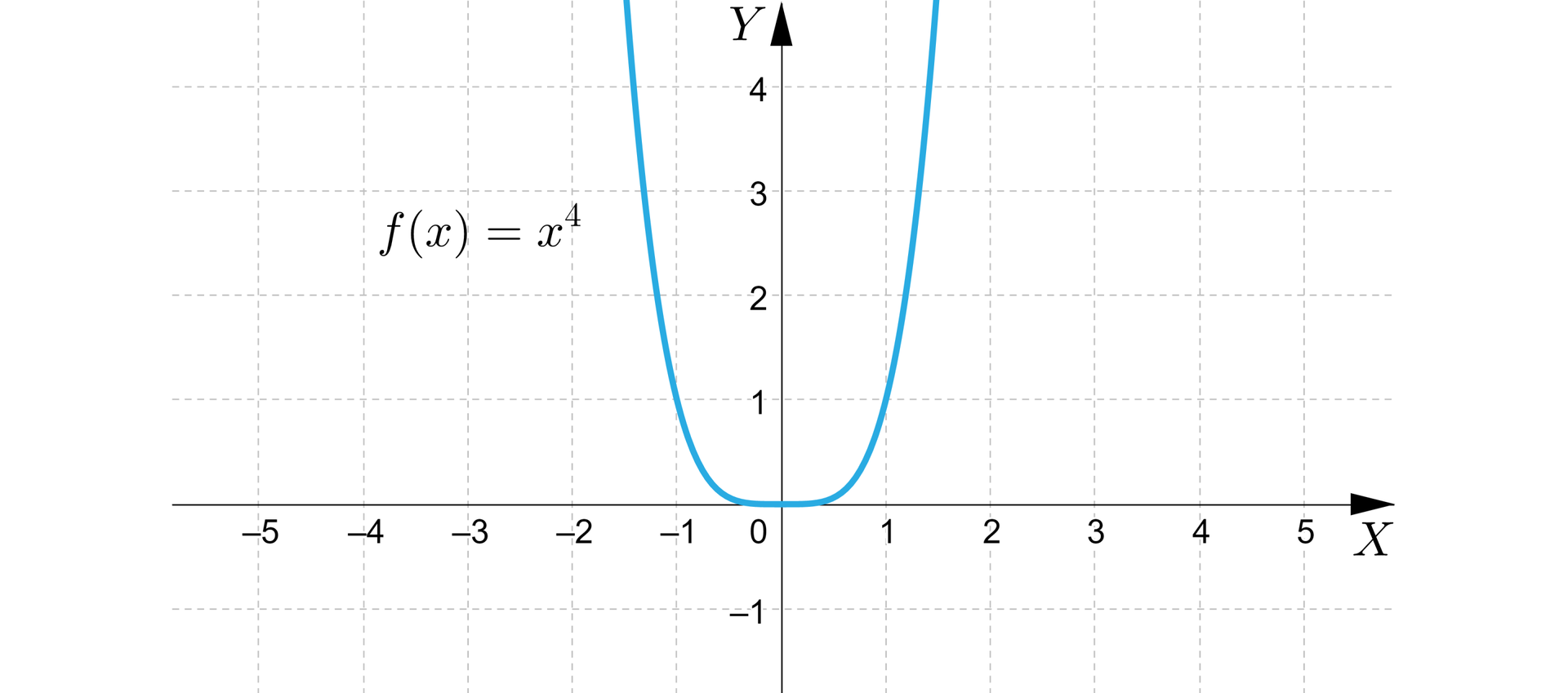

   Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji o równaniu $f\left(x\right)=x^4$. Pojawia się on w drugiej ćwiartce układu i biegnie delikatnie po łuku przez punkt nawias minus jeden średnik jeden zamknięcie nawiasu, następnie wypłaszcza się na osi x, przechodzi przez środek układu współrzędnych, dalej biegnie również po łuku przez punkt nawias jeden średnik jeden zamknięcie nawiasu i wychodzi poza płaszczyznę układu w pierwszej ćwiartce.

   

   Własności funkcji, której wykres przedstawiono na rysunku:

   • funkcja jest malejąca w przedziale $\left(-\infty ,0\right.⟩$ oraz rosnąca w przedziale $\left.⟨0,\infty \right)$,

   • funkcja nie jest różnowartościowa,

   • miejscem zerowym jest liczba $0$,

   • wartość najmniejsza funkcji wynosi $0$.

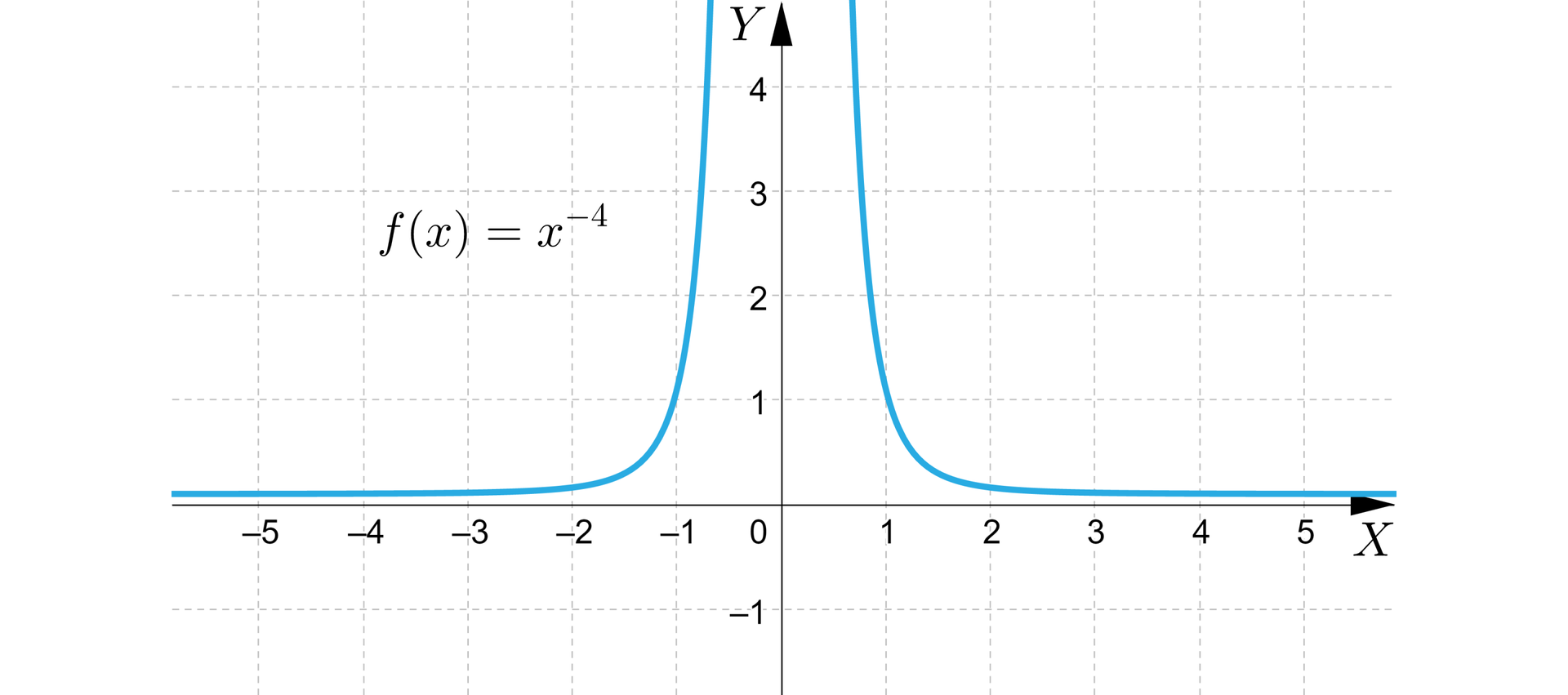
5. dla $m=2k+1$, gdzie $m$ jest liczbą całkowitą ujemną

   Funkcja jest określona wzorem $f\left(x\right)=x^{2k+1}$, gdzie $k\in {\mathrm{\mathbb{Z}}}_{-}$.

   Dziedziną i zbiorem wartości tej funkcji jest zbiór $\mathrm{ℝ}\setminus \left\{0\right\}$.

   Na przykład wykres funkcji określonej wzorem $f\left(x\right)=x^{-1}$ przedstawia się następująco:

   R1FY7CPHtGzC4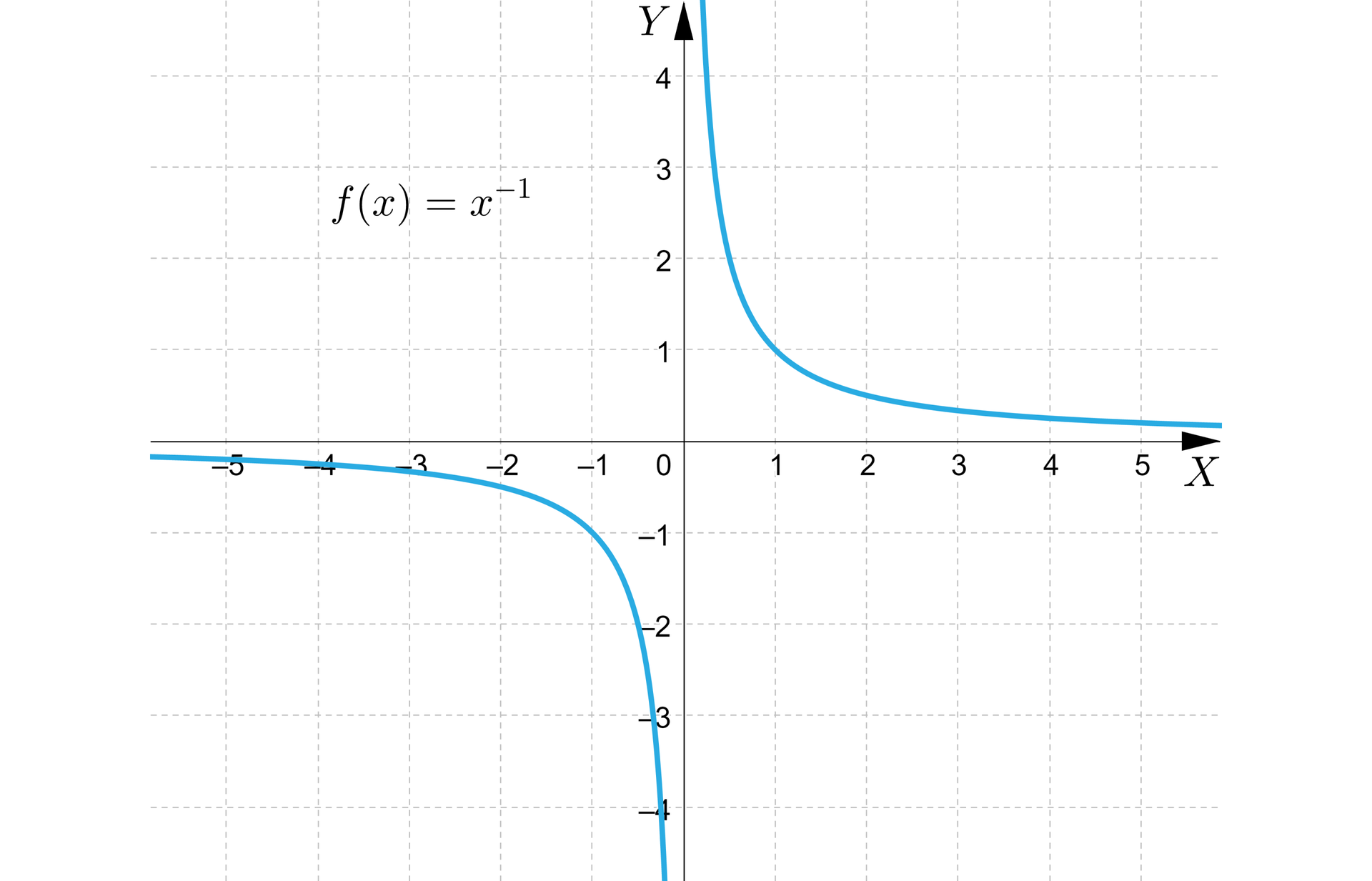

   Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 4 do cztery. W układzie zaznaczono wykres funkcji o równaniu $f\left(x\right)=x^{-1}$. Wykres ma kształt hiperboli, której asymptotami są osie układu współrzędnych. Pierwsza część znajduje się w całości w trzeciej ćwiartce i przechodzi przez punkt nawias minus jeden średnik minus jeden zamknięcie nawiasu. Druga część znajduje się w całości w pierwszej ćwiartce i przechodzi przez punkt nawias jeden średnik jeden zamknięcie nawiasu.

   

   Własności funkcji, której wykres przedstawiono na rysunku:

   • funkcja jest malejąca w przedziałach $\left(-\infty ,0\right)$ oraz $\left(0,\infty \right)$,

   • funkcja jest różnowartościowa,

   • funkcja nie ma miejsc zerowych,

   • funkcja nie ma wartości najmniejszej oraz wartości największej,

   • asymptotami wykresu funkcji są proste o równaniach $x=0$ oraz $y=0$.

6. $m=2k$, gdzie $m$ jest liczbą całkowitą ujemną

   Funkcja jest określona wzorem $f\left(x\right)=x^{2k}$, gdzie $k\in {\mathrm{\mathbb{Z}}}_{-}$.

   Dziedziną tej funkcji jest zbiór $\mathrm{ℝ}\setminus \left\{0\right\}$, a zbiorem wartości zbiór liczb rzeczywistych dodatnich.

   Na przykład wykres funkcji określonej wzorem $f\left(x\right)=x^{-2}$ przedstawia się następująco:

   R1PtM9O33uqCe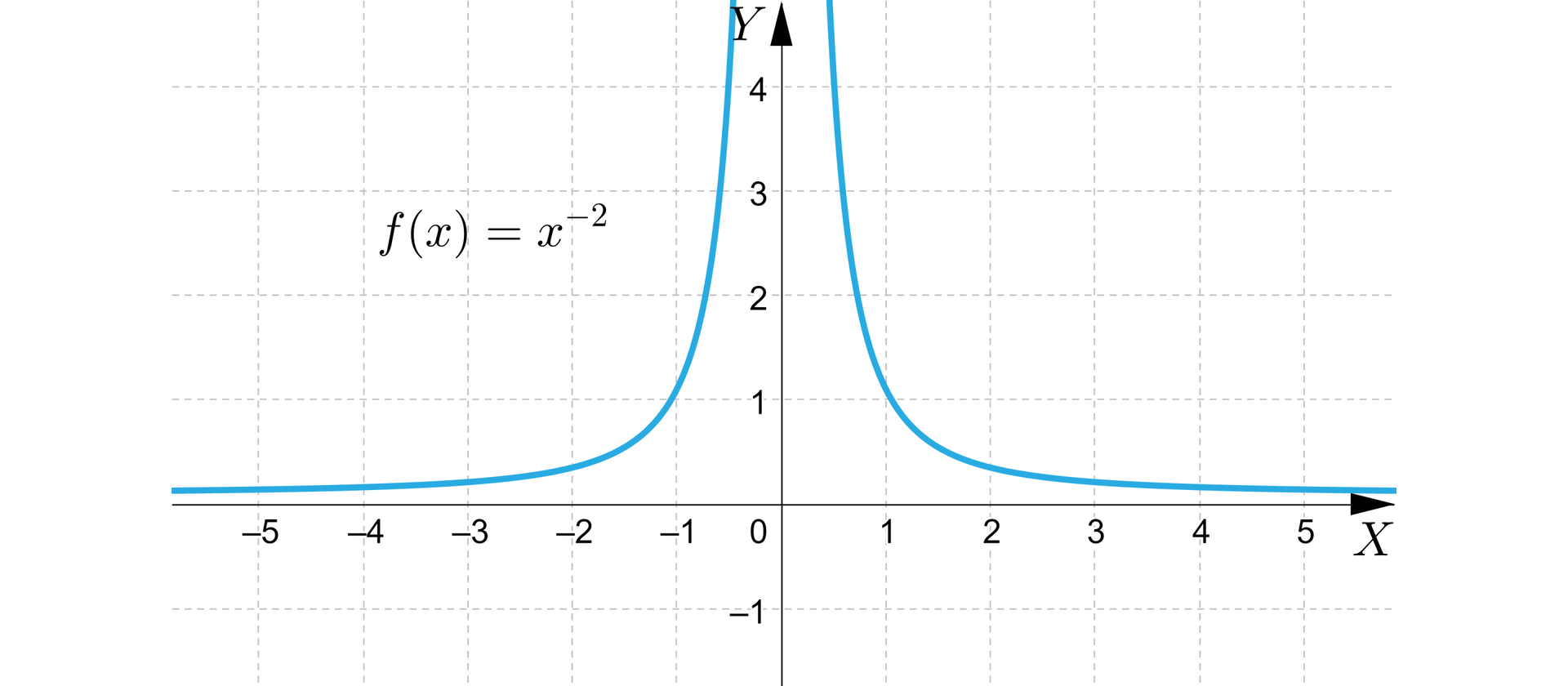

   Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji o równaniu $f\left(x\right)=x^{-2}$. Wykres ma kształt hiperboli, której pierwsza część została odbita symetrycznie wobec osi X. Asymptotami są osie układu współrzędnych. Pierwsza część znajduje się w całości w drugiej ćwiartce i przechodzi przez punkt nawias minus jeden średnik jeden zamknięcie nawiasu i jest rosnąca. Druga część znajduje się w całości w pierwszej ćwiartce i przechodzi przez punkt nawias jeden średnik jeden zamknięcie nawiasu i jest malejąca.

   

   Własności funkcji, której wykres przedstawiono na rysunku:

   • funkcja jest rosnąca w przedziale $\left(-\infty ,0\right)$ oraz malejąca w przedziale $\left(0,\infty \right)$,

   • funkcja nie jest różnowartościowa,

   • funkcja nie ma miejsc zerowych,

   • funkcja nie ma wartości najmniejszej oraz wartości największej,

   • asymptotami wykresu funkcji są proste o równaniach $x=0$ oraz $y=0$.

7. dla $m\in {ℝ}_{+}\setminus \mathrm{Z}$

   Funkcja jest określona wzorem $f\left(x\right)=x^m$, gdzie $m\in {ℝ}_{+}\setminus \mathrm{Z}$.

   Dziedziną i zbiorem wartości tej funkcji jest zbiór liczb rzeczywistych nieujemnych.

   Na przykład wykres funkcji określonej wzorem $f\left(x\right)=x^{\frac{1}{2}}$ przedstawia się następująco:

   R5I6CgUA33TUp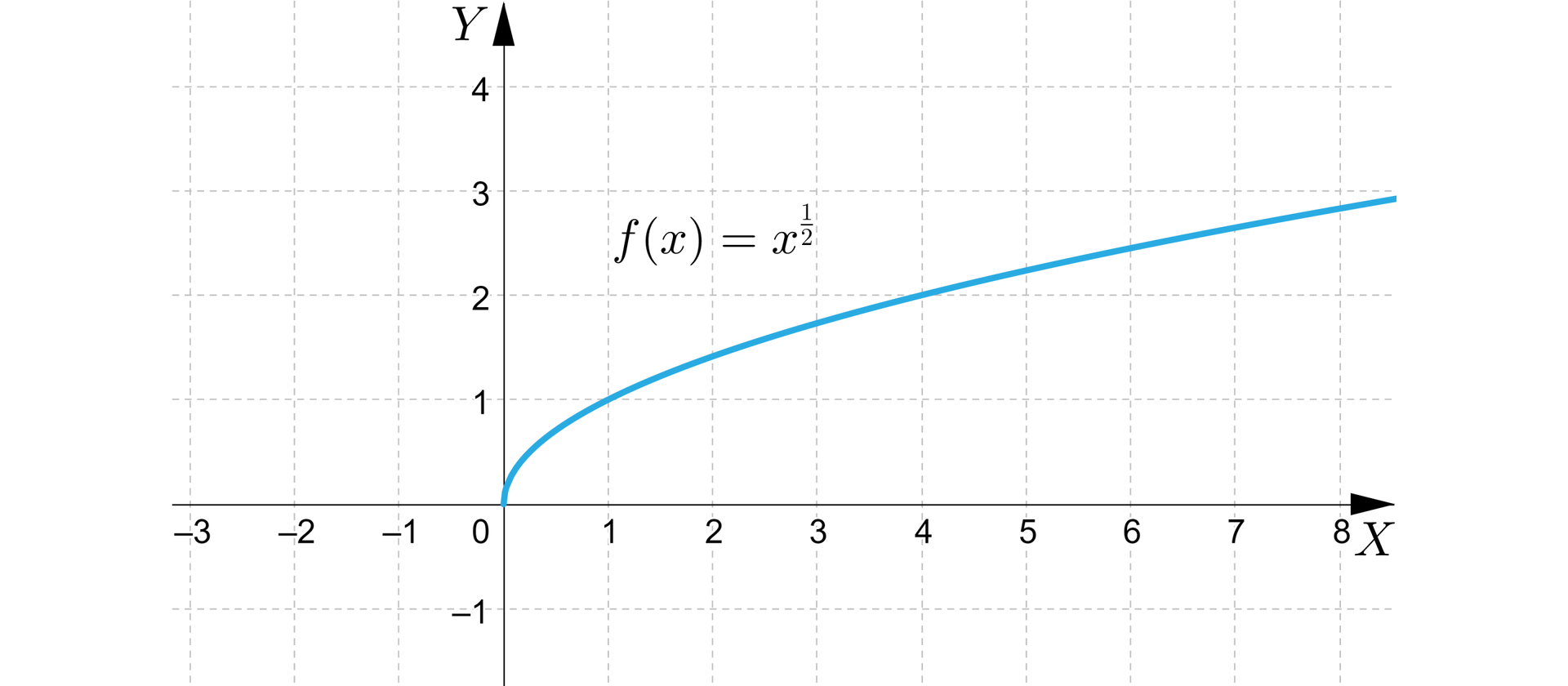

   Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji o równaniu $f\left(x\right)=x^{\frac{1}{2}}$. Wykres ma swój początek w środku układu współrzędnych i dalej biegnie po łuku przez punkty nawias jeden średnik jeden zamknięcie nawiasu i nawias cztery średnik dwa zamknięcie nawiasu i wychodzi poza płaszczyznę układu w pierwszej ćwiartce.

   

   Własności funkcji, której wykres przedstawiono na rysunku:

   • funkcja jest rosnąca w przedziale $\left.⟨0,\infty \right)$,

   • funkcja jest różnowartościowa,

   • miejscem zerowym funkcji jest liczba $0$,

   • funkcja nie ma wartości największej.

8. dla $m\in {ℝ}_{-}\setminus \mathrm{Z}$

   Funkcja jest określona wzorem $f\left(x\right)=x^m$, gdzie $m\in {ℝ}_{-}\setminus \mathrm{Z}$.

   Dziedziną i zbiorem wartości tej funkcji jest zbiór liczb rzeczywistych dodatnich.

   Na przykład wykres funkcji określonej wzorem $f\left(x\right)=x^{-\frac{1}{2}}$ przedstawia się następująco:

   RO8rjtuzdAW5c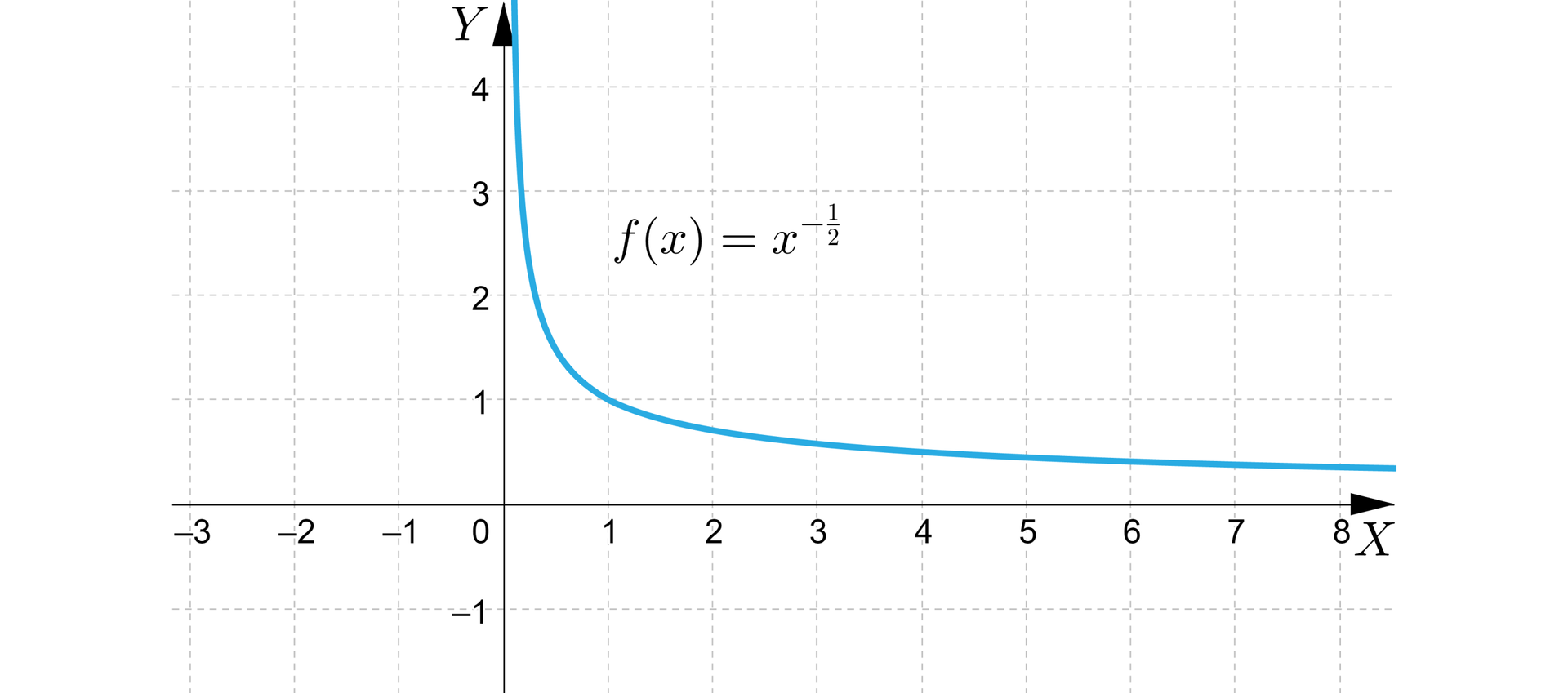

   Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 3 do 8 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji o równaniu $f\left(x\right)=x^{-\frac{1}{2}}$. Wykres ma pojawia się w pierwszej ćwiartce układu ryś przy osi y i biegnie po łuku przez punkt nawias jeden średnik jeden zamknięcie nawiasu, wychodzi poza płaszczyznę układu w pierwszej ćwiartce tuż nad osią x.

   

   Własności funkcji, której wykres przedstawiono na rysunku:

   • funkcja jest malejąca w przedziale $\left(0,\infty \right)$,

   • funkcja jest różnowartościowa,

   • funkcja nie ma miejsc zerowych,

   • funkcja nie ma wartości najmniejszej oraz wartości największej,

   • asymptotami wykresu funkcji są proste o równaniach $x=0$ oraz $y=0$.

Przykład 1

Na rysunku przedstawiono wykres funkcji określonej wzorem $f\left(x\right)=x^{\frac{1}{3}}$.

R19EYURQrClWb

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 3 do trzy. W układzie zaznaczono wykres funkcji o równaniu $f\left(x\right)=x^{\frac{1}{3}}$. Wykres pojawia się w  trzeciej ćwiartce układu i biegnie po łuku przez punkt nawias minus jeden średnik minus jeden zamknięcie nawiasu przez środek układu współrzędnych, dalej biegnie również po łuku przez punkt nawias jeden średnik jeden zamknięcie nawiasu i wychodzi poza płaszczyznę układu w pierwszej ćwiartce.

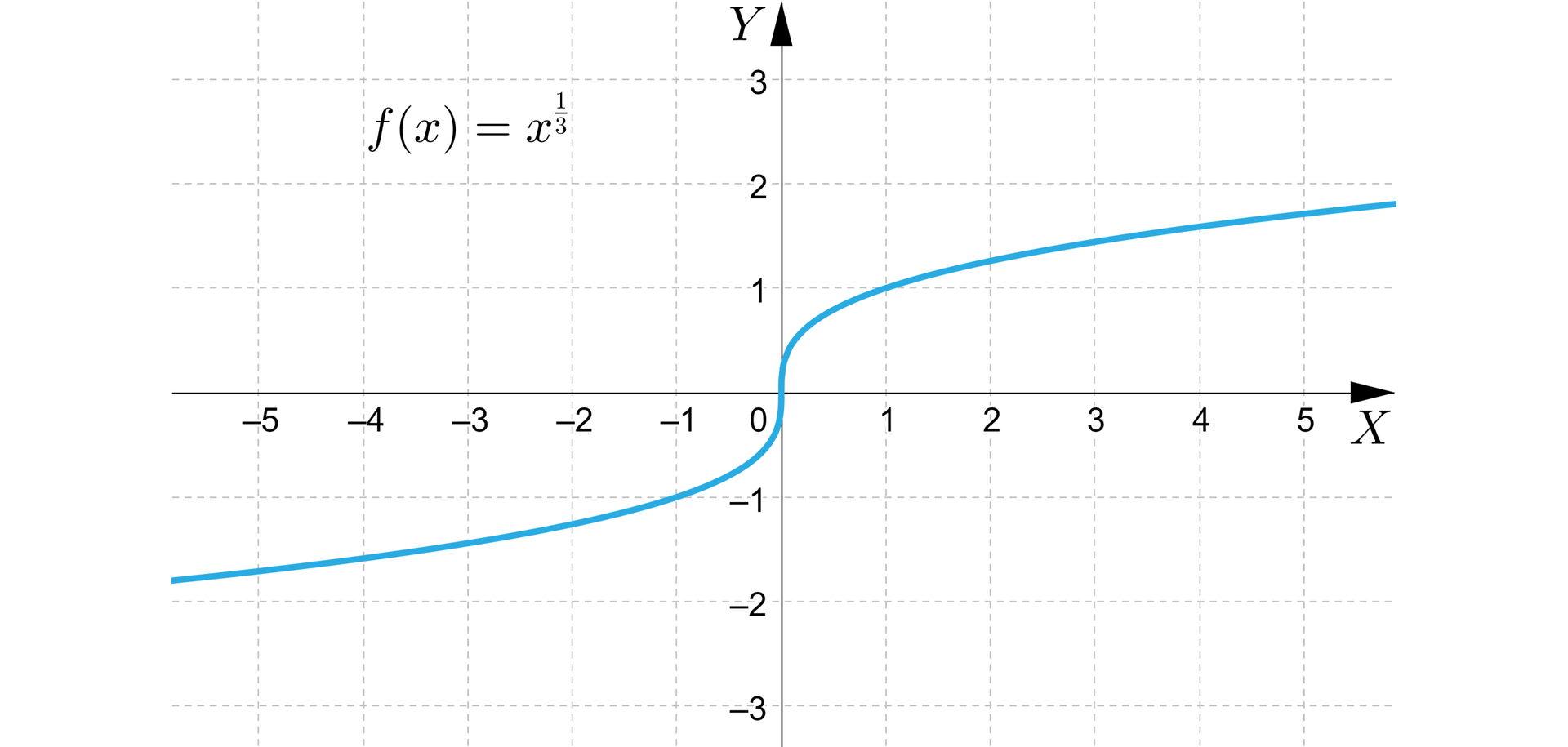
Odczytamy kilka różnych własności tej funkcji.

Rozwiązanie:

Odczytujemy z wykresu podstawowe własności tej funkcji:

• dziedziną funkcji jest zbiór liczb rzeczywistych,

• zbiorem wartości jest zbiór liczb rzeczywistych,

• funkcja nie ma wartości najmniejszej oraz wartości największej,

• funkcja jest rosnąca w całej swojej dziedzinie,

• funkcja jest różnowartościowa,

• funkcja przyjmuje wartości mniejsze od $0$ dla argumentów mniejszych od $0$,

• funkcja przyjmuje wartości większe od $0$ dla argumentów większych  od $0$,

• miejscem zerowym funkcji jest liczba $0$.

Przykład 2

Na rysunku przedstawiono wykres funkcji określonej wzorem $f\left(x\right)=x^m$.

R1OjDYNmPAbbr

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 4 do cztery. W układzie zaznaczono wykres funkcji o równaniu $f\left(x\right)=x^3$. Pojawia się on w trzeciej ćwiartce układu i biegnie delikatnie po łuku przez punkt nawias minus jeden średnik minus jeden zamknięcie nawiasu, następnie występuje wypłaszczenie na osi x i funkcja przechodzi przez środek układu współrzędnych następnie biegnie po łuku przez punkt nawias jeden średnik jeden zamknięcie nawiasu i wychodzi poza płaszczyznę układu w pierwszej ćwiartce. Na wykresie zaznaczono zamalowanymi kropkami następujące punkty: nawias minus dwa średnik minus osiem zamknięcie nawiasu i nawias dwa średnik osiem zamknięcie nawiasu.

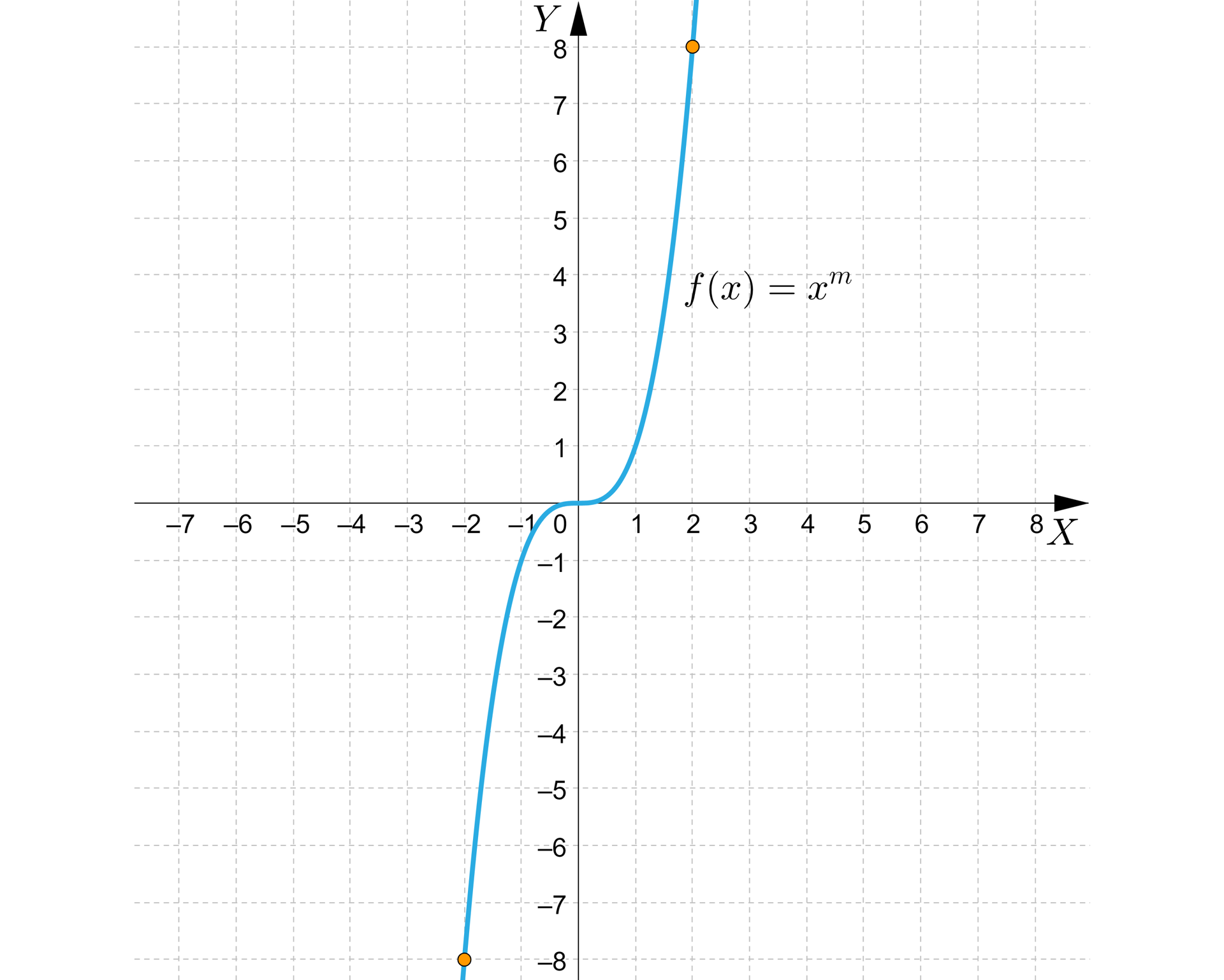
Wyznaczymy wzór tej funkcji, a następnie określimy:

a) dziedzinę i zbiór wartości,

b) argumenty, dla których funkcja przyjmuje wartości dodatnie oraz ujemne.

Rozwiązanie:

Zauważmy, że do wykresu funkcji określonej wzorem $f\left(x\right)=x^m$ należą punkty o współrzędnych $\left(2,8\right)$ oraz $\left(-2,-8\right)$.

Do wyznaczenia wartości $m$ rozwiązujemy równanie:

$8=2^m$, zatem $m=3$

a) dziedziną i zbiorem wartości funkcji z wykresu jest zbiór liczb rzeczywistych,

b) $f\left(x\right)<0$ dla $x<0$,
$f\left(x\right)>0$ dla $x>0$.

Przykład 3

Na rysunku przedstawiono wykres funkcji określonej wzorem $f\left(x\right)=x^{-\frac{1}{2}}$.

RQ7i2iRhIRV3c

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 3 do 8 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji o równaniu $f\left(x\right)=x^{-\frac{1}{2}}$. Wykres ma pojawia się w pierwszej ćwiartce układu ryś przy osi y i biegnie po łuku przez punkt nawias jeden średnik jeden zamknięcie nawiasu, wychodzi poza płaszczyznę układu w pierwszej ćwiartce tuż nad osią x.

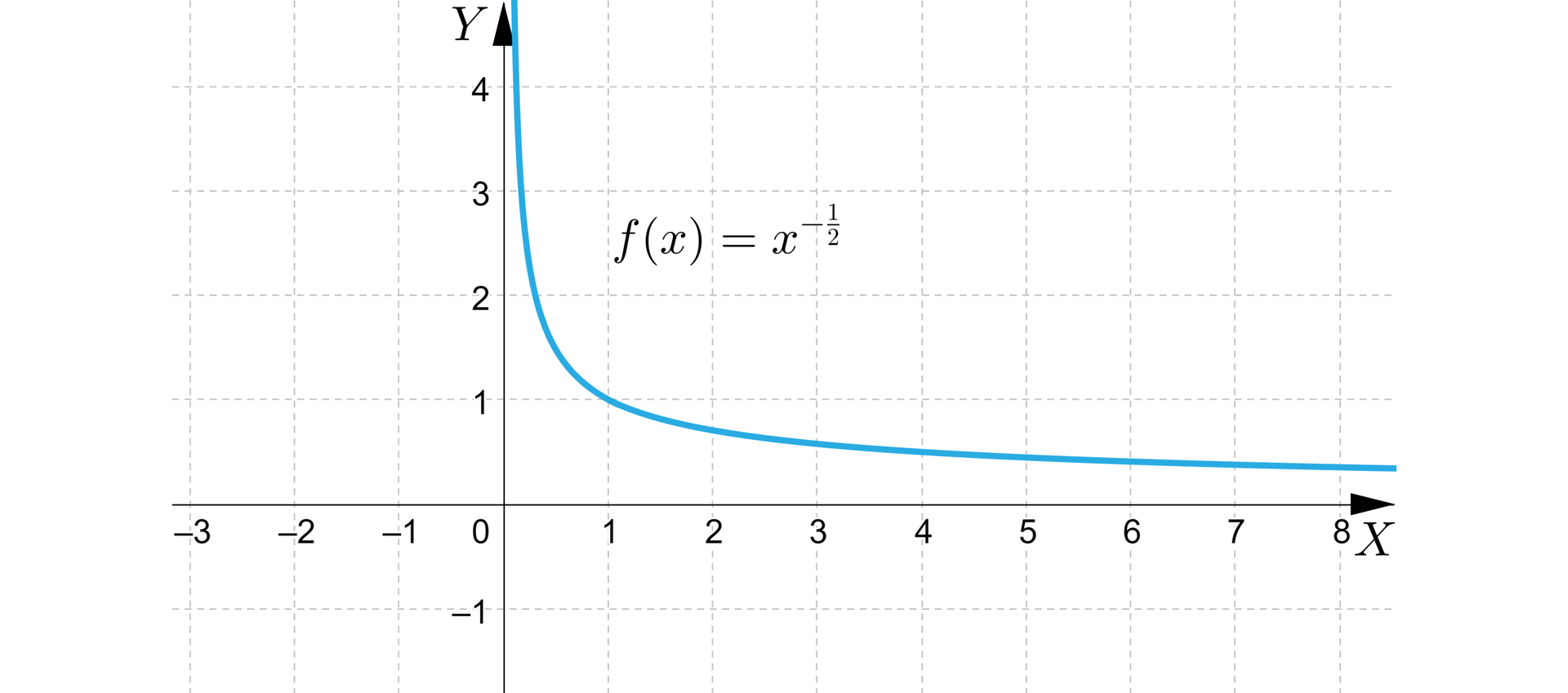
Wyznaczymy:

a) dziedzinę i zbiór wartości tej funkcji,

b) wartości funkcji dla argumentów $4$ i $16$,

c) argumenty, dla których funkcja przyjmuje wartości większe od $1$.

Rozwiązanie:

a) dziedziną i zbiorem wartości funkcji jest zbiór liczb rzeczywistych dodatnich,

b) obliczamy:

$f\left(4\right)=4^{-\frac{1}{2}}=\frac{1}{4^{{\displaystyle \frac{1}{2}}}}=\frac{1}{2}$

$f\left(4\right)={16}^{-\frac{1}{2}}=\frac{1}{{16}^{{\displaystyle \frac{1}{2}}}}=\frac{1}{4}$,

c) z wykresu funkcji odczytujemy, że $f\left(x\right)>1$ dla $x\in \left(0,1\right)$.

Podobnie jak w przypadku innych funkcji, na wykresach funkcji potęgowych można wykonywać różne przekształcenia.

Przykład 4

Na rysunku przedstawiono wykres funkcji określonej wzorem $f\left(x\right)=x^{-4}$.

R1Km3iIYpSMc9

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji o równaniu $f\left(x\right)=x^{-4}$. Wykres ma kształt hiperboli, której pierwsza część została odbita symetrycznie wobec osi X. Asymptotami są osie układu współrzędnych. Pierwsza część znajduje się w całości w drugiej ćwiartce i przechodzi przez punkt nawias minus jeden średnik jeden zamknięcie nawiasu i jest rosnąca. Druga część znajduje się w całości w pierwszej ćwiartce i przechodzi przez punkt nawias jeden średnik jeden zamknięcie nawiasu i jest malejąca.

Naszkicujemy wykres funkcji $g\left(x\right)=-f\left(x\right)$, a następnie określimy:

a) dziedzinę i zbiór wartości funkcji $g$,

b) przedziały monotoniczności funkcji $g$.

Rozwiązanie:

Przekształcenie $-f\left(x\right)$ oznacza odbicie symetryczne wykresu funkcji $f$ względem osi $X$, zatem wykres funkcji $g$ przedstawia się następująco:

Rbl7wwrUZu2XP

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji o równaniu $g\left(x\right)=-f\left(x\right)$. Wykres ma kształt hiperboli, której asymptotami są osie układu współrzędnych. Pierwsza część znajduje się w całości w trzeciej ćwiartce i przechodzi przez punkt nawias minus jeden średnik minus jeden zamknięcie nawiasu. Druga część znajduje się w całości w czwartej ćwiartce i przechodzi przez punkt nawias jeden średnik minus jeden zamknięcie nawiasu.

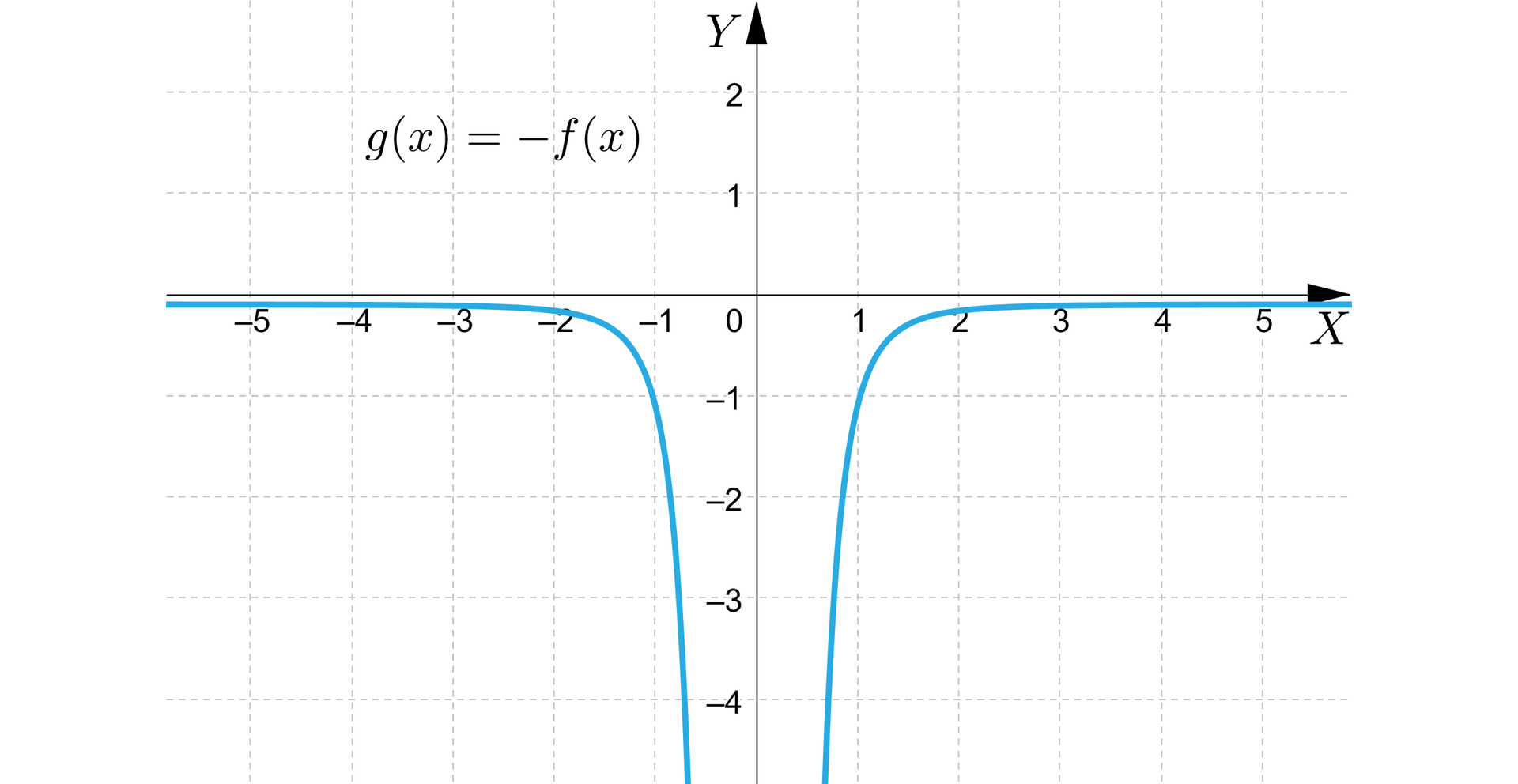
a) dziedziną funkcji $g$ jest zbiór liczb $\mathrm{ℝ}\setminus \left\{0\right\}$, a zbiorem wartości jest zbiór $\left(-\infty ,0\right)$,

b) funkcja $g$ jest malejąca w przedziale $\left(-\infty ,0\right)$ i rosnąca w przedziale $\left(0,\infty \right)$.

Przykład 5

Na rysunku przedstawiono wykresy funkcji określonych wzorami $f\left(x\right)=x^3$ oraz $g\left(x\right)=x^{-3}$.

RB0EIlb9M6fXq

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 4 do cztery. W układzie zaznaczono dwa wykresy. Pierwszy z nich ma równanie $f\left(x\right)=x^3$. Pojawia się on w trzeciej ćwiartce układu i biegnie delikatnie po łuku przez punkt nawias minus jeden średnik minus jeden zamknięcie nawiasu, następnie występuje wypłaszczenie na osi x i funkcja przechodzi przez środek układu współrzędnych następnie biegnie po łuku przez punkt nawias jeden średnik jeden zamknięcie nawiasu i wychodzi poza płaszczyznę układu w pierwszej ćwiartce. Wykres ten zaznaczono kolorem różowym. Drugi wykres ma równanie $g\left(x\right)=x^{-3}$. Wykres ma kształt hiperboli, której asymptotami są osie układu współrzędnych. Pierwsza część znajduje się w całości w trzeciej ćwiartce i przechodzi przez punkt nawias minus jeden średnik minus jeden zamknięcie nawiasu. Druga część znajduje się w całości w pierwszej ćwiartce i przechodzi przez punkt nawias jeden średnik jeden zamknięcie nawiasu.

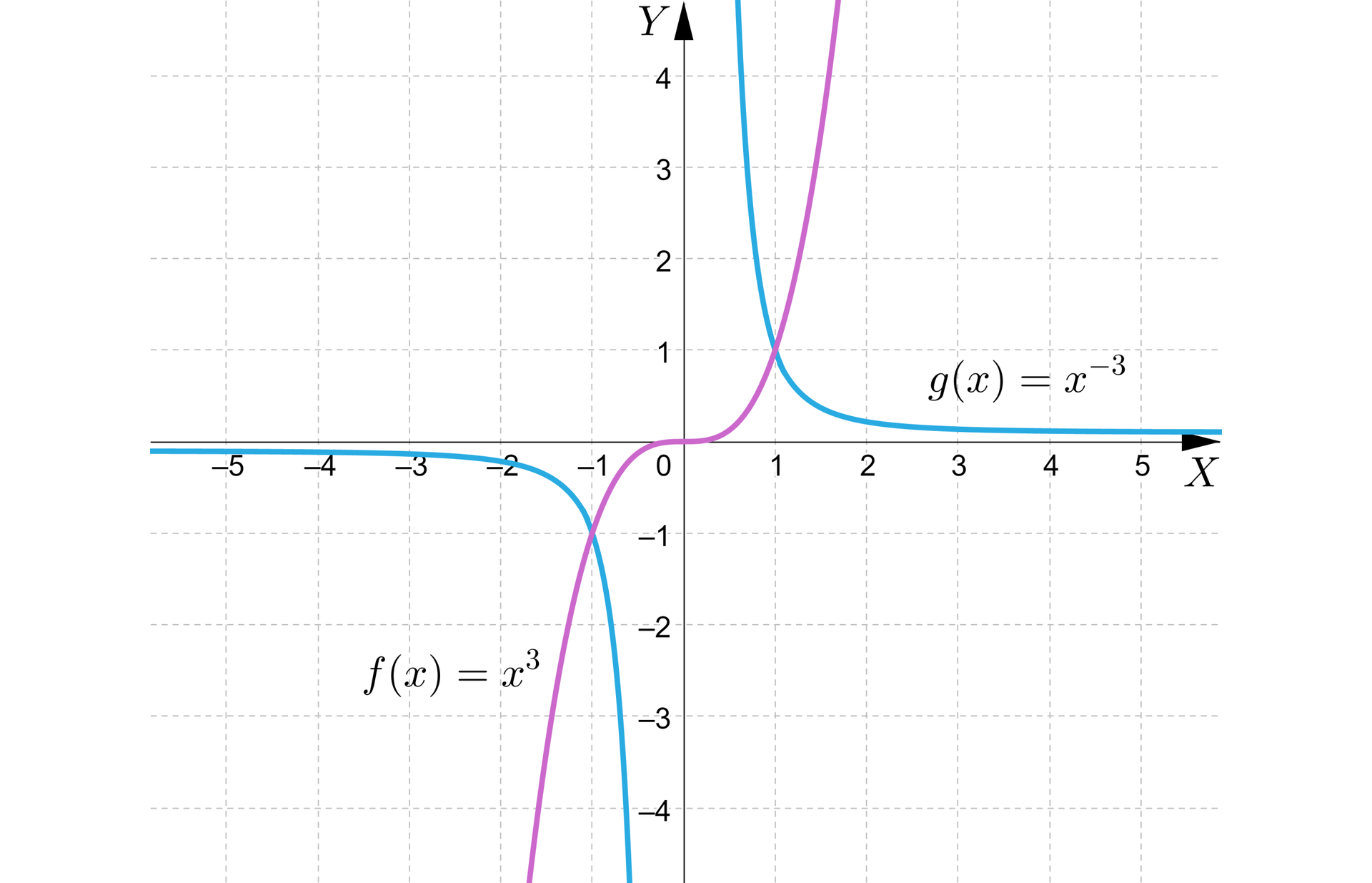
Na podstawie wykresu określimy rozwiązanie:

a) równania $f\left(x\right)=g\left(x\right)$,

b) nierówności $f\left(x\right)>g\left(x\right)$,

c) nierówności $f\left(x\right)<g\left(x\right)$.

Rozwiązanie:

a) $f\left(x\right)=g\left(x\right)$ dla $x\in \left\{-1,1\right\}$,

b) $f\left(x\right)>g\left(x\right)$ dla $x\in \left(-1,0\right)\cup \left(1,\infty \right)$,

c) $f\left(x\right)<g\left(x\right)$ dla $x\in \left(-\infty ,-1\right)\cup \left(0,1\right)$.

Słownik