Sprawdź się

Pokaż ćwiczenia:

RVPAxWQa2DKNw1

Ćwiczenie 1

Wskaż wzór funkcji, który nie przedstawia funkcji potęgowej:

$f (x) = 2^{x}$
$f (x) = x^{\frac{1}{2}}$
$f (x) = x^{- 2}$

Ćwiczenie 2

Rjmu5QXgOaE84

R1NbwiRlNilBI

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 5 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji

y = f (x)

. Wykres ma pojawia się w pierwszej ćwiartce układu przy osi y i biegnie po łuku przez punkt nawias jeden średnik jeden zamknięcie nawiasu, wychodzi poza płaszczyznę układu w pierwszej ćwiartce tuż nad osią x. Możliwe odpowiedzi: 1.

f (x) = x^{4}

, 2.

f (x) = x^{- 2}

, 3.

f (x) = x^{- \frac{1}{2}}

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 5 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji

y = f (x)

. Pojawia się on w drugiej ćwiartce układu i biegnie delikatnie po łuku przez punkt nawias minus jeden średnik jeden zamknięcie nawiasu, następnie wypłaszcza się na osi x, przechodzi przez środek układu współrzędnych, dalej biegnie również po łuku przez punkt nawias jeden średnik jeden zamknięcie nawiasu i wychodzi poza płaszczyznę układu w pierwszej ćwiartce. Możliwe odpowiedzi: 1.

f (x) = x^{4}

, 2.

f (x) = x^{- 2}

, 3.

f (x) = x^{- \frac{1}{2}}

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 5 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji

y = f (x)

. Wykres ma kształt hiperboli, której asymptotami są osie układu współrzędnych. Pierwsza część znajduje się w całości w drugiej ćwiartce i przechodzi przez punkt nawias minus jeden średnik jeden zamknięcie nawiasu. Druga część znajduje się w całości w pierwszej ćwiartce i przechodzi przez punkt nawias jeden średnik jeden zamknięcie nawiasu. Możliwe odpowiedzi: 1.

f (x) = x^{4}

, 2.

f (x) = x^{- 2}

, 3.

f (x) = x^{- \frac{1}{2}}

RKXfCgXMxbsdp1

Ćwiczenie 3

Pogrupuj elementy, zgodnie z podanym opisem. Własności funkcji potęgowej określonej wzorem

f (x) = x^{2}

: Możliwe odpowiedzi: 1. dziedziną funkcji jest zbiór liczb

ℝ

, 2. dziedziną funkcji jest zbiór

ℝ \ \{0\}

, 3. dla argumentu

2

funkcja przyjmuje wartość

4

, 4. dla argumentu

2

funkcja przyjmuje wartość

\frac{1}{4}

, 5. funkcja jest rosnąca w przedziale

(- \infty, 0 ⟩

, 6. funkcja jest malejąca w przedziale

(- \infty, 0)

Własności funkcji potęgowej określonej wzorem

f (x) = x^{- 2}

: Możliwe odpowiedzi: 1. dziedziną funkcji jest zbiór liczb

ℝ

, 2. dziedziną funkcji jest zbiór

ℝ \ \{0\}

, 3. dla argumentu

2

funkcja przyjmuje wartość

4

, 4. dla argumentu

2

funkcja przyjmuje wartość

\frac{1}{4}

, 5. funkcja jest rosnąca w przedziale

(- \infty, 0 ⟩

, 6. funkcja jest malejąca w przedziale

(- \infty, 0)

Pogrupuj elementy, zgodnie z podanym opisem.

dziedziną funkcji jest zbiór <math><mi mathvariant="normal">ℝ</mi><mo>∖</mo><mfenced open="{" close="}"><mn>0</mn></mfenced></math>, dziedziną funkcji jest zbiór liczb <math><mi mathvariant="normal">ℝ</mi></math>, dla argumentu <math><mn>2</mn></math> funkcja przyjmuje wartość <math><mfrac><mn>1</mn><mn>4</mn></mfrac></math>, funkcja jest rosnąca w przedziale <math><mfenced open="(" close="⟩"><mrow><mo>-</mo><mo>∞</mo><mo>,</mo><mn>0</mn></mrow></mfenced></math>, dla argumentu <math><mn>2</mn></math> funkcja przyjmuje wartość <math><mn>4</mn></math>, funkcja jest malejąca w przedziale <math><mfenced><mrow><mo>-</mo><mo>∞</mo><mo>,</mo><mn>0</mn></mrow></mfenced></math>

Własności funkcji potęgowej określonej wzorem $f (x) = x^{2}$ :
Własności funkcji potęgowej określonej wzorem $f (x) = x^{- 2}$ :

RbTsQHIvZE08p2

Ćwiczenie 4

Zaznacz zdania, które są prawdziwe.

Wykres funkcji określonej wzorem $f (x) = x^{- 3}$ znajduje się w $I$ i $III$ ćwiartce układu współrzędnych.
Funkcja określona wzorem $f (x) = x^{- 4}$ jest malejąca w całej swojej dziedzinie.
Funkcja określona wzorem $f (x) = x^{- 2}$ przyjmuje tylko wartości niedodatnie.
Zbiorem wartości funkcji określonej wzorem $f (x) = x^{- 3}$ jest zbiór liczb rzeczywistych.

RG6QAeIyxLOnx2

Ćwiczenie 5

Połącz w pary wzór funkcji ze współrzędnymi punktu, który należy do jej wykresu.

$f (x) = x^{- 1}$
$g (x) = x^{- \frac{1}{2}}$
$h (x) = x^{3}$
$k (x) = x^{\frac{1}{3}}$

Ćwiczenie 6

Na podstawie wykresu funkcji zaznacz zdanie, które jest prawdziwe.

RKaklD5drEy6w

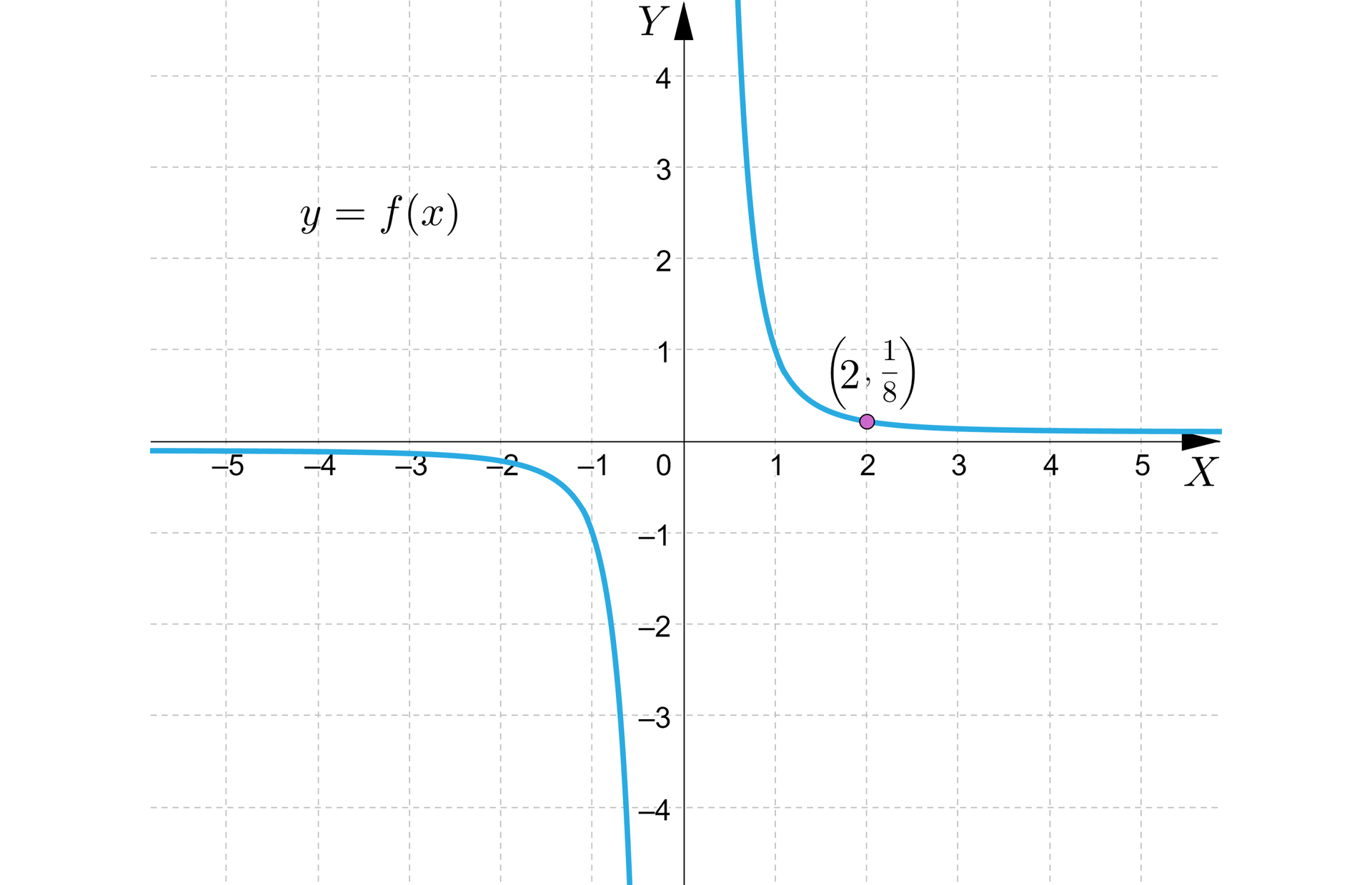
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 4 do cztery. W układzie zaznaczono wykres funkcji y=fx . Wykres ma kształt hiperboli, której asymptotami są osie układu współrzędnych. Pierwsza część znajduje się w całości w trzeciej ćwiartce i przechodzi przez punkt nawias minus jeden średnik minus jeden zamknięcie nawiasu. Druga część znajduje się w całości w pierwszej ćwiartce i przechodzi przez punkty nawias jeden średnik jeden zamknięcie nawiasu oraz nawias dwa średnik jedna czwarta zamknięcie nawiasu.

Rt3Oeqk4z9MLr

Ćwiczenie 7

Funkcja potęgowa określona jest wzorem $f (x) = x^{n}$ oraz $n \in ℕ$ . Wiadomo, że do wykresu tej funkcji należy punkt o współrzędnych $(\sqrt{2}, 4)$ .

Wyznacz:

a) wzór tej funkcji,

b) argumenty, dla których wartość funkcji wynosi $16$ .

a) Jeżeli do wykresu funkcji określonej wzorem $f (x) = x^{n}$ należy punkt o współrzędnych $(\sqrt{2}, 4)$ , to do wyznaczenia wartości $n$ rozwiązujemy równanie:

$4 = {(\sqrt{2})}^{n}$ , czyli $n = 4$ .

Wobec tego funkcja wyraża się wzorem $f (x) = x^{4}$ .

b) Do wyznaczenia argumentów, dla których funkcja przyjmuje wartość $16$ , rozwiązujemy równanie:

$16 = x^{4}$ , czyli $x = - 2$ oraz $x = 2$ .

Ćwiczenie 8

Na rysunku przedstawiono wykres funkcji $f (x) = x^{n}$ oraz wiadomo, że $n$ jest liczbą wymierną ujemną.

RCV0X1ylNpiZU

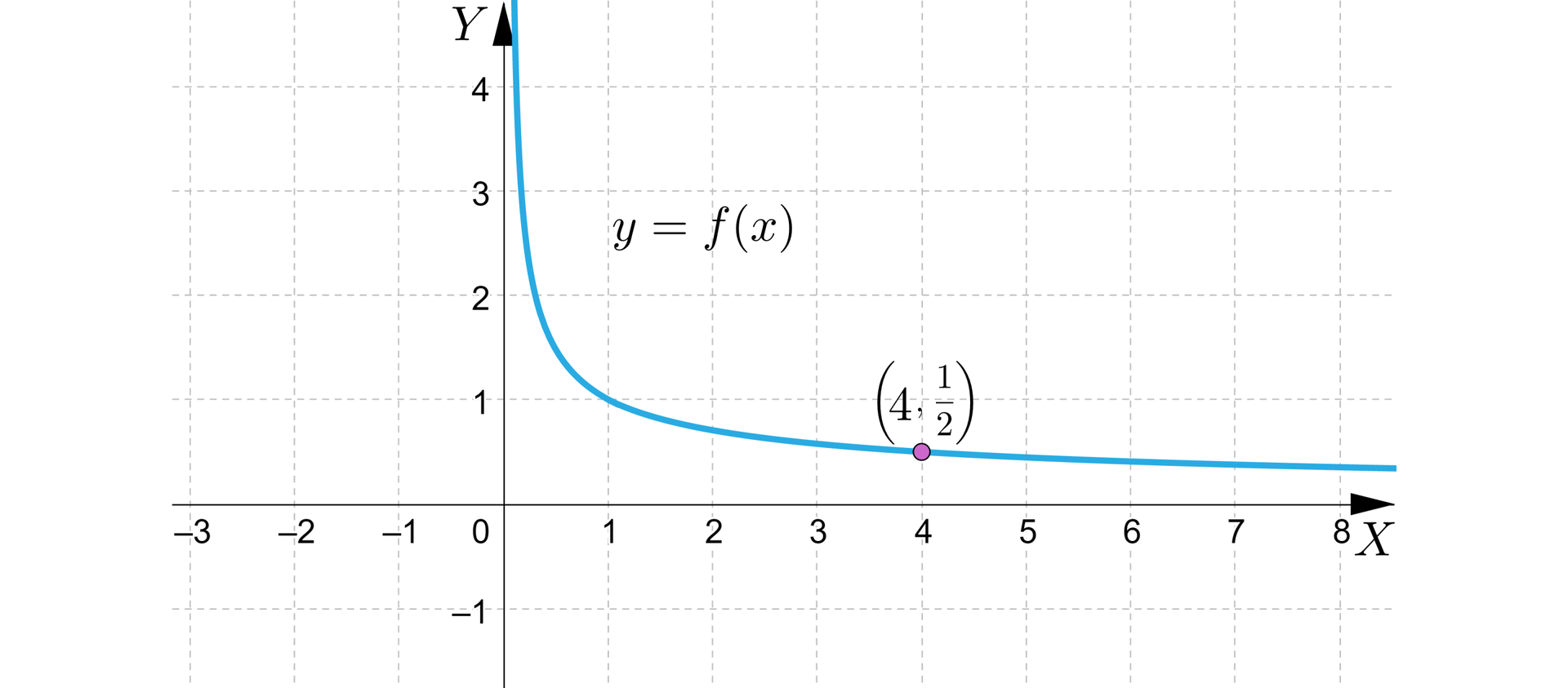
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 8 i pionową osią y od minus 1 do cztery. W układzie zaznaczono wykres funkcji y=fx . Wykres pojawia się w pierwszej ćwiartce układu przy osi y i biegnie po łuku przez punkty nawias jeden średnik jeden zamknięcie nawiasu i nawias cztery średnik jedna druga zamknięcie nawiasu i wychodzi poza płaszczyznę układu w pierwszej ćwiartce tuż nad osią x.

Wyznacz:

a) wzór tej funkcji,

b) argument, dla którego wartość funkcji wynosi $8$ ,

c) wartość tej funkcji dla argumentu $16$ .

a) Odczytujemy współrzędne punktu $(4, \frac{1}{2})$ , który należy do wykresu tej funkcji.

Do wyznaczenia wartości $n$ rozwiązujemy równanie:

$4^{n} = \frac{1}{2}$

$2^{2 n} = 2^{- 1}$ , czyli $n = - \frac{1}{2}$ .

Wobec tego funkcja jest określona wzorem $f (x) = x^{- \frac{1}{2}}$ .

b) Rozwiązujemy równanie:

$8 = x^{- \frac{1}{2}}$

$x = 8^{- 2} = \frac{1}{64}$ .

c) Obliczamy wartość funkcji dla argumentu $16$ :

$f (16) = 16^{- \frac{1}{2}} = {(4^{2})}^{- \frac{1}{2}} = 4^{- 1} = \frac{1}{4}$ .

Aplet

Dla nauczyciela