Aplet
Polecenie 1
Uruchom aplet, a następnie odczytaj różne własności funkcji wykładniczej. Wskaż argumenty dla kilku podanych wartości oraz wartości, jakie funkcja przyjmuje dla kilku wybranych argumentów.
Zapoznaj się z opisem apletu. Przeanalizuj podane przykłady. Jaki można wysnuć wniosek dotyczący podsatwy , a jego wpływu na własności badanej funckji?
- dziedziną jest zbiór liczb rzeczywistych
- zbiór wartości funckji jest przedziałem otwartym od zera do nieskończoności
- funkcja jest różnowartościowa
- brak miejsc zerowych
- asymptota wykresu:
- wykres znajduje się w pierwszej i drugiej ćwiartce układu współrzędnych
- funkcja przyjmuje wartości mniejsze od jeden dla argumentów mniejszych od zera
- funkcja przyjmuje wartości większe od 1 dla argumentów większych od zera Przykład 2. W układzie zaznaczono wykres funckji . Jest to krzywa wykładnicza rosnąca, która unosi się dla argumentów od minus nieskończoności lekko ponad oś X a następnie dla co raz większych argumentów przyjmuje co raz większe wartości tak, że wykres funckji przechodzi przez punkty oraz . Reszta opisu wykresu funckji nie ulega zmianie. Przykład 3. W układzie zaznaczono wykres funckji . Jest to krzywa wykładnicza rosnąca, która unosi się dla argumentów od minus nieskończoności lekko ponad oś X a następnie dla co raz większych argumentów przyjmuje co raz większe wartości tak, że wykres funckji przechodzi przez punkty oraz . Reszta opisu wykresu funckji nie ulega zmianie.
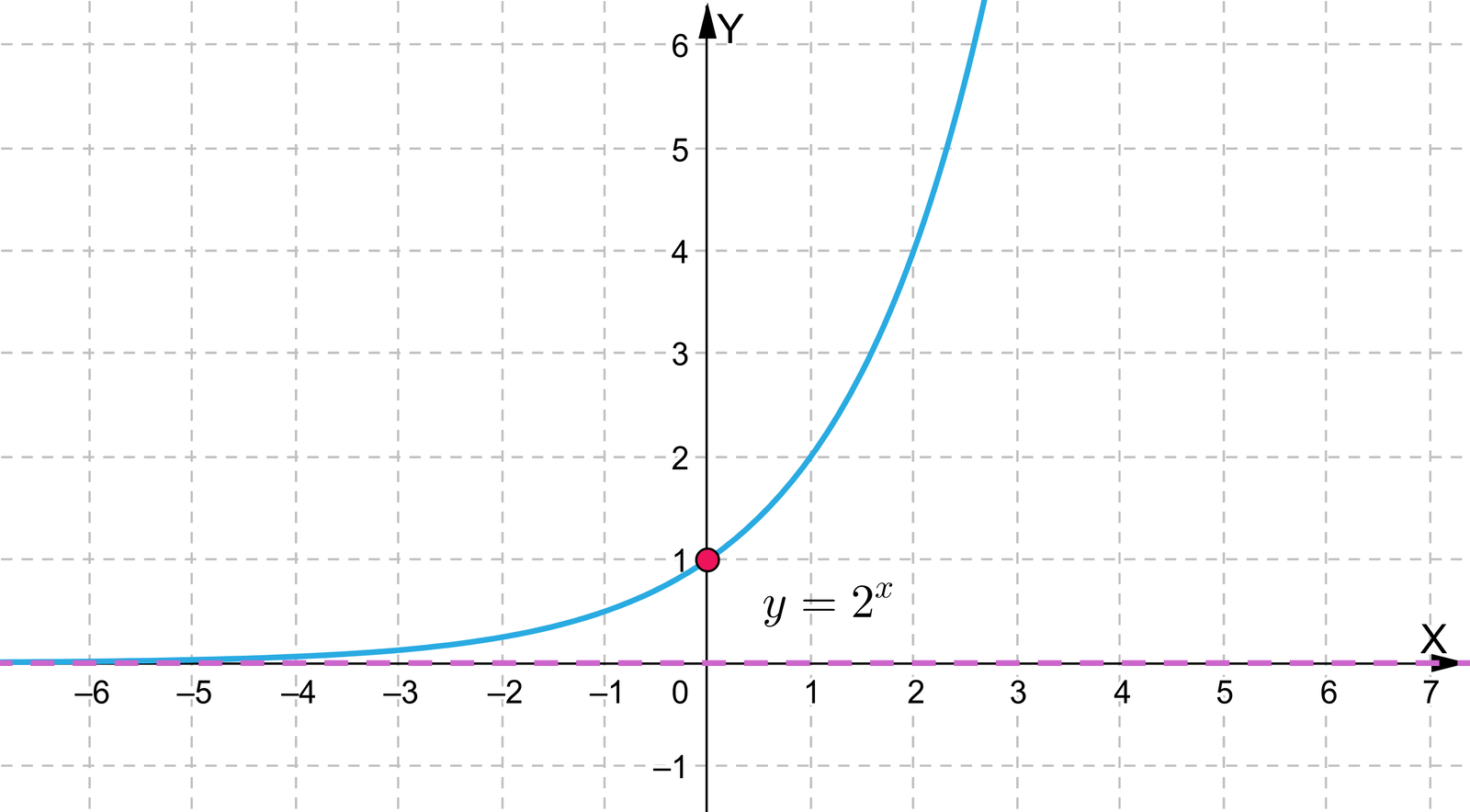
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DyzYFgEtq
Polecenie 2
Określamy funkcję wykładniczą wzorem .
Wyznacz wartość parametru , jeżeli do wykresu tej funkcji należy punkt o współrzędnych .