Przeczytaj

Funkcja wykładnicza

Definicja: Funkcja wykładnicza

Funkcję określoną na zbiorze liczb rzeczywistych wzorem

f (x) = a^{x},

gdzie
$a > 0$ i $a \neq 1$ , nazywamy funkcją wykładniczą

Omówimy własności funkcji wykładniczejfunkcja wykładniczafunkcji wykładniczej określonej wzorem $f (x) = a^{x}$ , gdzie $a \in (1, \infty)$ .

Wykresem funkcji wykładniczej jest krzywa wykładnicza.

Naszkicujemy wykres funkcji wykładniczej zadanej wzorem $f (x) = 3^{x}$ . W tym celu obliczymy najpierw wartości tej funkcji dla kilku argumentów.

$x$	$- 2$	$- 1$	$0$	$1$	$2$
$f (x)$	$\frac{1}{9}$	$\frac{1}{3}$	$1$	$3$	$9$

Wykres funkcji przedstawia się następująco:

R1LPs0AG0VmAo

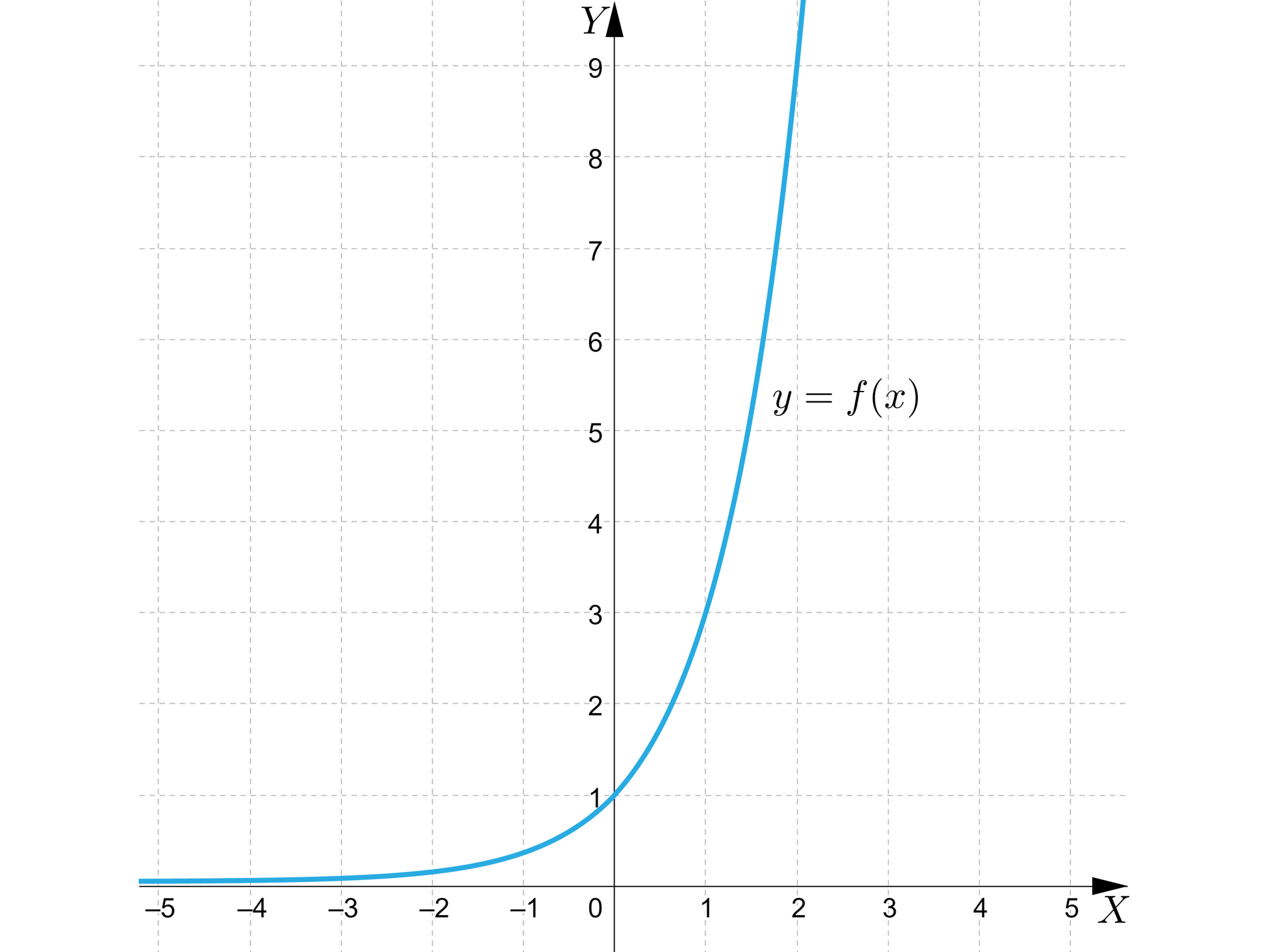
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus pięciu do pięciu oraz z pionową osia Y od zera do dziewięciu. W układzie zaznaczono wykres funckji y=fx. Jest to krzywa wykładnicza rosnąca, której asymptotą poziomą jest prosta y=0. Wykres przechodzi przez punkty 0,1 oraz 1,3.

Dla funkcji wykładniczej określonej wzorem $y = a^{x}$ , gdzie $a \in (1, \infty)$ , zachodzą następujące własności:

dziedziną funkcji jest zbiór liczb rzeczywistych,
zbiorem wartości funkcji jest zbiór liczb rzeczywistych dodatnich, tzn. $y \in (0, \infty),$
funkcja jest rosnąca,
funkcja jest różnowartościowa,
funkcja nie ma miejsc zerowych,
asymptotą wykresu funkcji jest prosta $y = 0$ ,
wykres funkcji przechodzi przez punkt $(0, 1)$ ,
wykres funkcji znajduje się w $I$ i $II$ ćwiartce układu współrzędnych,
funkcja przyjmuje wartości mniejsze od $1$ dla argumentów mniejszych od $0$ ,
funkcja przyjmuje wartości większe od $1$ dla argumentów większych od $0$ .

Niektóre z powyższych własności wynikają z następujących faktów:

potęga dowolnej liczby dodatniej jest liczbą dodatnią,

dwie potęgi o tych samych podstawach (różnych od $0$ i $1$ ) są sobie równe, gdy mają te same wykładniki,

każda liczba, różna od $0$ , podniesiona do potęgi $0$ jest równa $1$ .

Przykład 1

Wyznaczymy dziedzinę funkcji określonej wzorem $f (x) = {(3 \sqrt{3})}^{x}$ , jeżeli zbiorem jej wartości jest przedział $⟨\frac{1}{3}, 9⟩$ .

Rozwiązanie:

Z uwagi na to, że funkcja jest różnowartościowa i rosnąca, do wyznaczenia dziedziny funkcji wystarczające jest wyznaczenie argumentów odpowiadających wartościom funkcji na krańcach przedziału.

Do wyznaczenia dziedziny funkcji rozwiązujemy równania:

${(3 \sqrt{3})}^{x} = \frac{1}{3}$ , więc $x = - \frac{2}{3}$ .

${(3 \sqrt{3})}^{x} = 9$ , więc $x = \frac{4}{3}$ .

Dziedziną podanej funkcji jest przedział

$⟨- \frac{2}{3}, \frac{4}{3}⟩$ .

Przykład 2

Na rysunku przedstawiono wykres funkcji wykładniczej określonej wzorem $f (x) = a^{x}$ . Wyznaczymy wzór tej funkcji oraz obliczymy, dla jakiego argumentu funkcja przyjmuje wartość $\frac{1}{2}$ .

RilsrkHL3cnlS

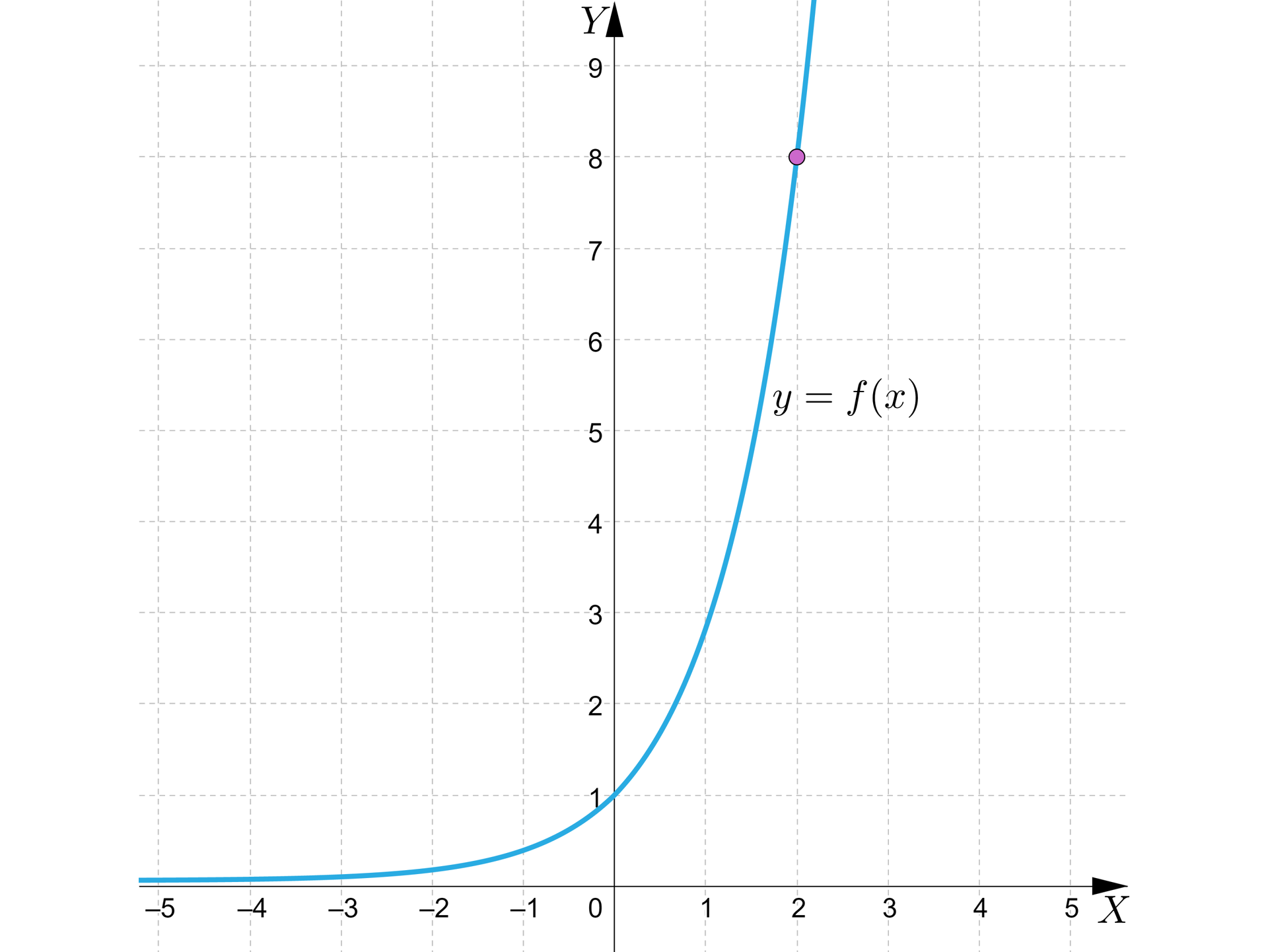
Rozwiązanie:

Z rysunku odczytujemy, że do wykresu tej funkcji należy punkt o współrzędnych $(2, 8)$ .

W celu wyznaczenia wartości $a$ , rozwiązujemy równanie $a^{2} = 8$ .

Z równania otrzymujemy, że $a = 2 \sqrt{2}$ lub $a = - 2 \sqrt{2}$ .

Ponieważ $a > 0$ , więc $a = 2 \sqrt{2}$ .

Funkcja jest określona wzorem $f (x) = {(2 \sqrt{2})}^{x}$ .

Do wyznaczenia argumentu, dla którego funkcja przyjmuje wartość $\frac{1}{2}$ , rozwiązujemy równanie:

${(2 \sqrt{2})}^{x} = \frac{1}{2}$ .

Równanie zapisujemy w postaci $2^{\frac{3}{2} x} = 2^{- 1}$ .

Funkcja jest różnowartościowa, zatem $x = - \frac{2}{3}$ .

Przykład 3

Wyznaczymy zbiór wartości funkcji określonej wzorem $f (x) = {(\sqrt{3} + 1)}^{x}$ , jeżeli $x \in ⟨- 1, 2⟩$ .

Rozwiązanie:

Funkcja jest różnowartościowa i rosnąca, wystarczy zatem obliczyć wartości funkcji na końcach podanego przedziału.

Zatem mamy:

$f (- 1) = {(\sqrt{3} + 1)}^{- 1} = \frac{1}{\sqrt{3} + 1} = \frac{\sqrt{3} - 1}{2}$ .

$f (2) = {(\sqrt{3} + 1)}^{2} = 3 + 2 \sqrt{3} + 1 = 4 + 2 \sqrt{3}$ .

Zbiorem wartości podanej funkcji jest przedział $⟨\frac{\sqrt{3} - 1}{2}, 4 + 2 \sqrt{3}⟩$ .

Wiedząc o tym, kiedy funkcja wykładnicza jest rosnąca, możemy wyznaczać wartości parametrów, które występują we wzorze tej funkcji.

Przykład 4

Wyznaczymy, dla jakich wartości parametru $m$ , funkcja wykładnicza określona wzorem $f (x) = {(12 m^{2} + m)}^{x}$ jest rosnąca.

Rozwiązanie:

Funkcja wykładniczafunkcja wykładniczaFunkcja wykładnicza określona wzorem $f (x) = a^{x}$ jest rosnąca, gdy $a > 1$ .

Ponieważ dla każdej funkcji wykładniczej $a > 0$ , zatem $12 m^{2} + m > 0$ .

Rozwiązaniem nierówności jest zbiór $m \in (- \infty, - \frac{1}{12}) \cup (0, \infty)$ .

Jeżeli $a > 1$ , to $12 m^{2} + m > 1$ .

Po rozwiązaniu powyższej nierówności i wyznaczeniu części wspólnej otrzymanych zbiorów, uzyskujemy odpowiedź:

$m \in (- \infty, - \frac{1}{3}) \cup (\frac{1}{4}, \infty)$ .

Przykład 5

Wyznaczymy, dla jakich wartości parametru $m$ , punkt o współrzędnych $(2, 4)$ należy do wykresu funkcji wykładniczej określonej wzorem $f (x) = {(m - 3)}^{x}$ .

Rozwiązanie:

Dla funkcji wykładniczej $f (x) = a^{x}$ zachodzi warunek: $a > 0$ .

Wobec tego $m - 3 > 0$ , czyli $m > 3$ .

Jeżeli punkt o współrzędnych $(2, 4)$ należy do wykresu funkcji $f$ , to do wyznaczenia wartości parametru $m$ rozwiązujemy równanie:

${(m - 3)}^{2} = 4$ .

Równanie przekształcamy do postaci $m - 3 = 2$ lub $m - 3 = - 2$ .

Zatem $m = 5$ lub $m = 1$ .

Z warunku, że $m > 3$ otrzymujemy, że $m = 5$ .

Słownik

funkcja wykładnicza

funkcja określona wzorem $f (x) = a^{x}$ , gdzie podstawa potęgi jest ustaloną liczbą dodatnią $a$ , różną od $1$

Wprowadzenie

Aplet

Słownik