Audiobook
Posłuchaj o dokonaniach Smoluchowskiego
Wysłuchaj informacji o naukowych dokonaniach wybitnego polskiego fizyka - Mariana Smoluchowskiego, a następnie wykonaj zaproponowane poniżej polecenia. Pomogą Ci one w utrwaleniu zdobytych informacji.
Opracuj prosty model „błądzenia przypadkowego” (tak Smoluchowski potraktował ruchy Browna) i przeprowadź symulację takiego błądzenia.
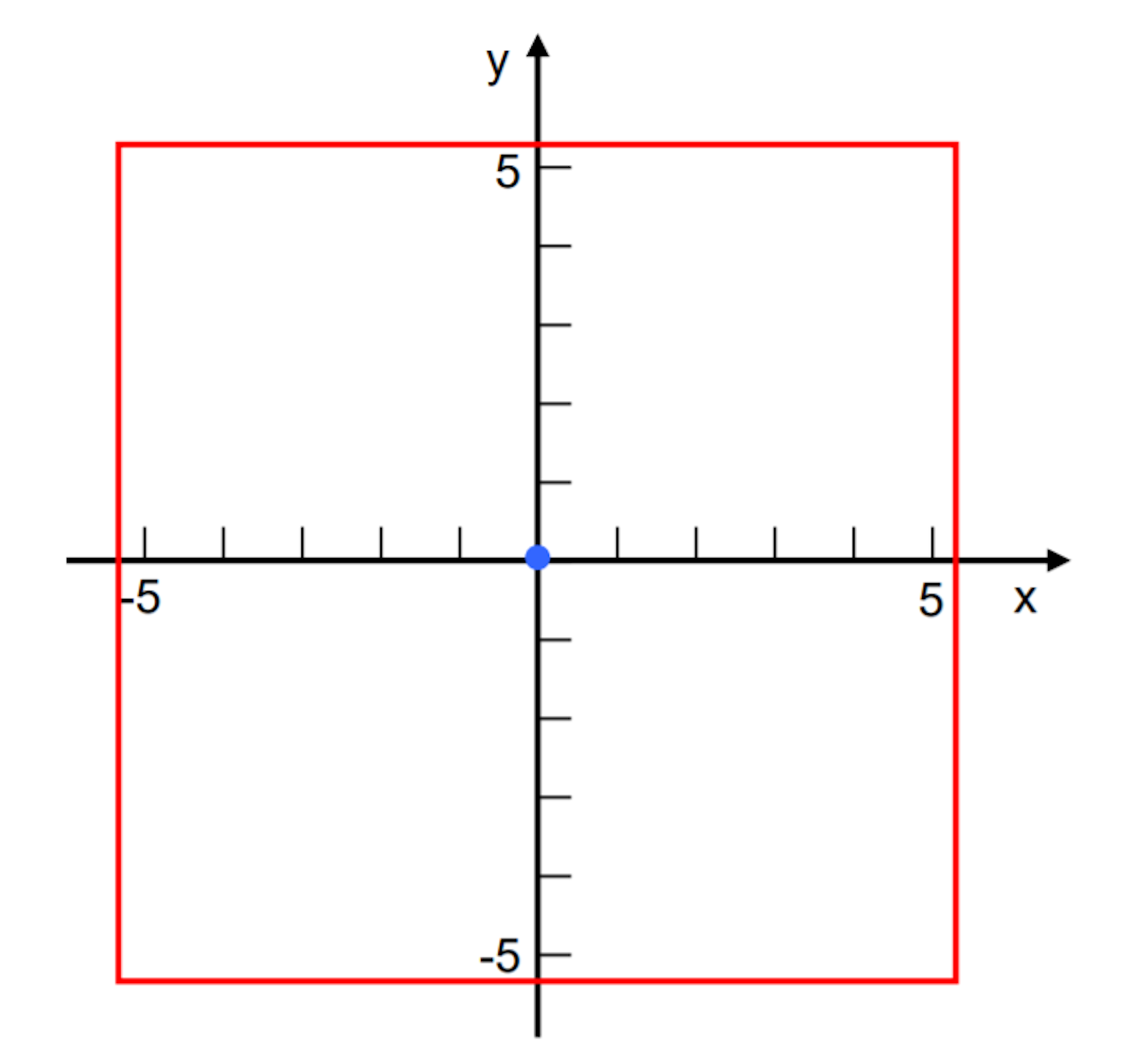
Model polega na śledzeniu jednowymiarowego ruchu punktu materialnego, który może przeskakiwać losowo, z jednakowym prawdopodobieństwem do góry i do dołu, pomiędzy sąsiednimi położeniami na osi y układu współrzędnych. Na poniższym rysunku przyjęto, że liczba N dostępnych w modelu położeń jest równa 11 (5 w górę, pięć w dół oraz 0) . Czerwone kreski wskazują granice dopuszczalnych położeń.
Przyjmij, że upływ czasu t w tym modelu będzie odmierzany kolejnymi rzutami monety.
Przyjmij, że początkowe położenie yIndeks dolny 00 = 0.
Zasada „przypadkowego błądzenia” w Twoim modelu polega na tym, że po wyrzucie orła, punkt przesuwa się w górę osi y o jedną jednostkę, zaś po wyrzucie reszki o jedną jednostkę w dół.
Symulacja zakończy się, gdy położenie punktu osiągnie wartość y = 6 lub y = -6.
Sporządź wykres zależności położenia y od czasu t – jest on jednym z wyników Twojej symulacji. Innym wynikiem jest liczba rzutów R, po których punkt „opuszcza model”.

Przeanalizuj wyniki następującej symulacji:
Liczba dostępnych położeń punktu: N = 11
Wykres zależności y(t):

Punkt opuścił model w 18 rzucie; R = 18.
Porównaj te wyniki z wynikami swojej symulacji. Wskaż i zaklasyfikuj podobieństwa pomiędzy tymi wynikami. Określ, czy te podobieństwa będą występowały we wszystkich takich symulacjach (konieczne), tylko w niektórych (dopuszczalne) czy też takie podobieństwa nie mogą występować (wykluczone).
konieczne dopuszczalne wykluczone
tendencja przemieszczania się punktu w kierunku położeń ujemnych.
konieczne dopuszczalne wykluczone
tendencja przemieszczania się punktu wyłącznie w kierunku położeń dodatnich bądź ujemnych
konieczne dopuszczalne wykluczone
Wartość R = 18
konieczne dopuszczalne wykluczone
Wartość R = 6
konieczne dopuszczalne wykluczone
Wartość R = 7
konieczne dopuszczalne wykluczone
przypadkowy przebieg zmian położenia
{#konieczne} {dopuszczalne} {wykluczone}
tendencja przemieszczania się punktu w kierunku położeń ujemnych.
{konieczne} {#dopuszczalne} {wykluczone}
tendencja przemieszczania się punktu wyłącznie w kierunku położeń dodatnich bądź ujemnych
{konieczne} {#dopuszczalne} {wykluczone}
Wartość R = 18
{konieczne} {#dopuszczalne} {wykluczone}
Wartość R = 6
{konieczne} {#dopuszczalne} {wykluczone}
Wartość R = 7
{konieczne} {dopuszczalne} {#wykluczone}
Opracuj podobny model „błądzenia przypadkowego”, tym razem w dwóch wymiarach, N x N, dla N = 11. Określ sposób losowania przeskoku punktu materialnego w taki sposób, by ruchy w obu kierunkach x i y były od siebie niezależne oraz by zapewnić jednakowe prawdopodobieństwa, w każdym z tych kierunków, trzech wydarzeń: zwiększenia położenia o jeden, pozostania w miejscu, zmniejszenia położenia o jeden. Każda taka para (deltax; deltay) to upływ jednej (umownej) jednostki czasu symulacji.
Przygotuj odpowiednią planszę. Rozważ wykorzystanie w tym celu odpowiedniego programu graficznego lub pola wykresu w arkuszu kalkulacyjnym.
Przeprowadź symulację takiego błądzenia.
Zaznaczaj kropką kolejne położenia błądzącego punktu w układzie współrzędnych; łącz te położenia odcinkami ze strzałką.
Wynikiem symulacji będzie:
tor błądzącego punktu,
liczba R umownych jednostek czasu, po których punkt opuścił planszę,
położenie, z którego opuścił planszę.
Namów koleżanki lub kolegów, by przeprowadzili podobną dwuwymiarową symulację przypadkowego błądzenia punktu. Porównajcie wyniki. Przedyskutujcie podobieństwa i różnice pomiędzy nimi.
Odsłuchaj ponownie fragment audiobooka, w którym mowa jest o ilościowym badaniu ruchów Browna przez Jeana Perrina. Notował on położenia cząstek zawiesiny w jednakowych odstępach czasu, rzędu minut, a nawet dziesiątek minut. W tym czasie cząstka doznawała wielu „elementarnych popchnięć” ze strony cząsteczek cieczy.
Przeprowadź dwuwymiarową symulację według nieco odmiennych zasad, niż obowiązywały w poprzedniej:
nie ograniczaj zakresu dopuszczalnych położeń punktu,
zapisuj w tabeli położenia punktu po kolejnych losowaniach,
przeprowadź kilkadziesiąt, do stu nawet, takich losowań,
na planszy o odpowiednio dobranych rozmiarach, ujawnij nie wszystkie położenia punktu, lecz po każdych pięciu kolejnych losowaniach.
Porównaj uzyskany obraz z oryginalnymi wynikami Perrina, przedstawionymi na poniższym rysunku.

Smoluchowski potraktował ruchy Browna jako błądzenie przypadkowe (zwane też błądzeniem losowym). Stworzymy teraz poglądowy model tego procesu i przeprowadzimy jego symulacje.
Błądzenie przypadkowe może przyjąć bardzo wiele różnych form. Na przykład, jeżeli chcemy zasymulować błądzenie losowe cząstki w jednym wymiarze, to najprościej jest taki model oprzeć na następujących założeniach.
Pierwszym z nich jest dyskretność czasudyskretność czasu. Warto podkreślić, że nie jest to kluczowe założenie dla modelu błądzenia losowego cząstki - jest to w tym przypadku pewne uproszczenie, które znacznie ułatwi nam stworzenie modelu i analizę wyników.
Kolejne założenie dotyczy samego ruchu cząstki. Ponieważ tworzony przez nas model jest jednowymiarowy, to zakładamy, że w każdym kroku czasowym cząstka może poruszyć się jedynie w lewo lub w prawo. Kierunek ruchu jest wybierany całkowicie losowo (stąd nazwa „błądzenie losowe”) z jednakowym prawdopodobieństwem i żaden nie jest wyróżniony. Oznacza to, że prawdopodobieństwo wyboru dla każdego z kierunków wynosi 0,5. Po wyborze kierunku ruchu, cząstka przesuwa się o zadaną odległość, która jest parametrem modelu. Ponieważ zakładamy również, że ta odległość jest zawsze taka sama, to jej wartość nie jest istotna, gdyż wpływa jedynie na skalę.
Założenia te dają nam prosty model błądzenia losowego. Są one na tyle nieskomplikowane, że moglibyśmy, przy pomocy źródła losowości w postaci zwykłej monety lub kostki do gry, własnoręcznie przeprowadzić symulacje modelu i przeanalizować wyniki. Wynikiem pojedynczej symulacji byłaby sekwencja wyborów kierunku ruchu. Dzięki niej bylibyśmy w stanie, dodając do siebie poszczególne przesunięcia, odtworzyć położenia cząstki w każdym kroku czasowym. My jednak nie zasymulujemy modelu błądzenia przypadkowego w dokładnie takiej postaci. Zrobimy coś innego - przeniesiemy ten model w świat dźwięków.
Niech w modelu dźwiękowym położeniu cząstki odpowiada częstotliwość sinusoidalnego sygnału. Częstotliwością początkową, będącą analogią początkowego położenia cząstki, jest 400 Hz. W każdym kroku czasowym dochodzi do zwiększenia lub zmniejszenia częstotliwości, przy czym prawdopodobieństwa obu tych zdarzeń są jednakowe. Jest to analogia wyboru kierunku ruchu przez cząstkę. Częstotliwość zmienia się zawsze o 50 Hz, co jest analogią odległości pokonywanej przez cząstkę podczas każdego kroku. Te założenia dają nam model błądzenia losowego dźwięku, który jest całkowicie równoważny błądzeniu losowemu cząstki. Zauważ jednak jedną różnicę - w przypadku modelu dźwiękowego kroki czasowe nie mają oczywistej fizycznej interpretacji i odpowiadają jedynie kolejnym sygnałom dźwiękowym. Natomiast w przypadku ruchu cząstki, moglibyśmy te kroki wyskalować w sekundach.
Zapoznaj się z przedstawionymi dalej poleceniami, które pozwolą ci przeanalizować wyniki symulacji takiego modelu.
Zacznijmy od czegoś prostego. Wysłuchaj przedstawionej dalej sekwencji pięciu częstotliwości wygenerowanych zgodnie z regułami modelu błądzenia przypadkowego dźwięku. Spróbuj określić, jak jest ostatnia częstotliwość. Pamiętaj przy tym, że częstotliwości zmieniają się o 50 Hz, a pierwszy sygnał dźwiękowy to zawsze częstotliwość początkowa wynosząca 400 Hz.
Zauważ, że jeżeli chodzi o ostatnią częstotliwość, to w błądzeniu przypadkowym nie ma znaczenia kolejność zmian częstotliwości, a jedynie liczba tych zmian w każdym z możliwych kierunków. Wystarczy więc, że zapamiętasz, ile razy częstotliwość wzrosła (lub zmalała) i na tej podstawie możesz określić ostatnią częstotliwość.
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Spróbuj jeszcze raz odpowiedzieć na to samo pytanie. Wysłuchaj kolejnego sygnału dźwiękowego wygenerowanego przez model dla pięciu kroków czasowych i określ ostatnią częstotliwość.
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Czy jest możliwe, aby na końcu dziesięciokrokowej symulacji modelu błądzenia przypadkowego dźwięku uzyskać częstotliwość 950 Hz? Pamiętaj, że pierwszemu krokowi czasowemu zawsze odpowiada częstotliwość początkowa wynosząca 400 Hz.
Teraz nieco bardziej skomplikowany sygnał, składający się z dziesięciu dźwięków. Jaka będzie ostatnia częstotliwość w tym przypadku?
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
W sygnale z poprzedniego polecenia, po dziewięciu zmianach częstotliwości dźwięku, ostatnia wartość częstotliwości była jedynie o 50 Hz mniejsza od poziomu początkowego. Czy taki wynik jest zgodny z oczekiwaniami? A może należałoby się spodziewać większej zmiany?
W tym poleceniu zawarto 10 sygnałów, będących wynikami 6 kroków symulacji modelu błądzenia losowego dźwięku. Dla każdego z nich określ częstotliwość końcową i uśrednij te wartości. Czy ten wynik potwierdza intuicję stojącą za odpowiedzią na pytanie postawione w poprzednim problemie?
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Wysłuchaj następującej sekwencji dźwięków.
Nagranie dostępne pod adresem https://zpe.gov.pl/a/DLpYv1ydd
Wysłuchaj ścieżki dźwiękowej.
Czy taka sekwencja jest zgodna z założeniami modelu błądzenia losowego dźwięku?
Na koniec warto podkreślić, że wszystkie wnioski, który wyciągnęliśmy na podstawie dźwiękowego modelu błądzenia losowego, dotyczą również modelu błądzenia losowego cząstki. Pamiętajmy, że choć w pierwszym z tych modeli rozważamy zmiany częstotliwości, a w drugim zmiany położenia, to oba modele są sobie efektywnie równoważne.
Słowniczek
(ang.: discrete time) Dyskretność jest, w tym kontekście, przeciwieństwem ciągłości. Dyskretny czas odmierzamy nie w sekundach, lecz w tak zwanych krokach czasowych, które mogą, choć nie muszą, odpowiadać pewnym „porcjom” czasu. Rzeczywista długość pojedynczego kroku czasowego zależy od specyfiki modelowanego zjawiska i związanych z nim skal czasu. W wielu modelach długość kroku nie ma jednak praktycznego znaczenia, a krok czasowy służy jedynie do numerowania kolejnych zdarzeń opisywanych w ramach danego modelu.
Inaczej na to patrząc, model z czasem dyskretnym określa stan pewnego układu na końcu każdego kroku czasowego i nie zajmuje się tym, co dzieje się pomiędzy poszczególnymi krokami. Dla przykładu, model epidemiologiczny z dyskretnym czasem mógłby nam mówić o liczbie zarażonych ludzi z pewnej populacji pod koniec każdego roku. Natomiast ciągły wariant takiego modelu dałby nam analogiczną informację - liczbę zarażonych ludzi - ale w każdej chwili.