Działania na liczbach dziesiętnych
Liczby dziesiętne – przypomnienie
Połącz w pary liczbę dziesiętną z odpowiednim opisem słownym.
<span aria-label="dwa przecinek jeden dwa" role="math"><math><mn>2</mn><mo>,</mo><mn>12</mn></math></span>, <span aria-label="zero przecinek zero trzy" role="math"><math><mn>0</mn><mo>,</mo><mn>03</mn></math></span>, <span aria-label="dwadzieścia przecinek zero dwa cztery" role="math"><math><mn>20</mn><mo>,</mo><mn>024</mn></math></span>, <span aria-label="zero przecinek trzy trzy" role="math"><math><mn>0</mn><mo>,</mo><mn>33</mn></math></span>, <span aria-label="dwa przecinek dwa zero" role="math"><math><mn>2</mn><mo>,</mo><mn>20</mn></math></span>, <span aria-label="zero przecinek trzy" role="math"><math><mn>0</mn><mo>,</mo><mn>3</mn></math></span>
| trzy dziesiąte | |
| trzydzieści trzy setne | |
| dwa i dwadzieścia setnych | |
| dwadzieścia i dwadzieścia cztery tysięczne | |
| trzy setne | |
| dwa i dwanaście setnych |
Przeciągnij i upuść cyfrę, która w liczbie jest cyfrą:
, , , , , ,
a) jedności ............
b) setek ............
c) dziesiątek ............
d) części setnych ............
e) części tysięcznych ............
f) części dziesiątych ............
Zamień ułamek zwykły na liczbę dziesiętną, a liczbę dziesiętną na ułamek zwykły.
Zapisz liczby dziesiętne w postaci nieskracalnych ułamków zwykłych.
Zapisz liczby dziesiętne w postaci nieskracalnych ułamków zwykłych lub liczb mieszanych.
Uporządkuj liczby rosnąco.
Uporządkuj liczby rosnąco.
Film dostępny na portalu epodreczniki.pl
Animacja
Pozycja cyfry po przecinku liczby dziesiętnej jest ważna.
Tabela przedstawia różne sposoby zapisu liczb dziesiętnych.
Zapis słowny | Ułamek dziesiętny(ułamek zwykły o mianowniku ) lub liczba mieszana | Liczba dziesiętna(zapis z przecinkiem) |
siedemnaście setnych | ||
trzy i sześć dziesiątych | ||
pięćset dziesięciotysięcznych | lub końcowe zera możemy opuścić |
Liczby dziesiętne można zapisać w postaci ułamków zwykłych.
Przy zamianie liczb dziesiętnych na ułamki zwykłe staramy się doprowadzić ułamki zwykłe do postaci nieskracalnej.
Ułamek zwykły, który da się rozszerzyć do ułamka o mianowniku , możemy zapisać w postaci liczby dziesiętnej.
Gdy porównujemy liczby dziesiętne, porównujemy kolejno: całości, części dziesiąte, części setne itd.
Jeśli liczby dziesiętne mają różną liczbę miejsc po przecinku, to możemy rozszerzyć jedną z liczb tak, aby obie miały taką samą liczbę miejsc po przecinku.
Dodawanie i odejmowanie liczb dziesiętnych
Film dostępny na portalu epodreczniki.pl
Animacja
Film dostępny na portalu epodreczniki.pl
Animacja
Oblicz w pamięci.
Oblicz w pamięci.
Oblicz w pamięci.
Dodawanie lub odejmowanie liczb dziesiętnych sposobem pisemnym wykonujemy podobnie jak pisemne dodawanie lub odejmowanie liczb naturalnych. Pamiętamy jednak, że musimy dodać lub odjąć całości do całości, części dziesiąte do dziesiątych, części setne do setnych itd. Wobec tego liczby trzeba zapisać tak, by przecinek drugiej liczby był pod przecinkiem pierwszej liczby.

Odejmując liczby i trzeba rozszerzyć liczbę dopisując na końcu .

Oblicz sposobem pisemnym.
Oblicz sposobem pisemnym .
Warszawskie Metro ma dwie linie. Pierwsza z nich przebiega przez dzielnice: Ursynów (pierwsza stacja na osiedlu Kabaty), Mokotów, Śródmieście, Żoliborz i Bielany (ostatnia stacja Młociny) , ma i stacji. Linia ta łączy południowe i północne dzielnice lewobrzeżnej Warszawy z centrum miasta. Druga linia Warszawskiego Metra przebiega przez dzielnice: Wola, Śródmieście i Praga, ma i stacji.
Metro w Wiedniu jest jednym z najstarszych systemów metra w Europie. W obecnym kształcie zaczęło funkcjonować i rozwijać się od roku, jednak zalążki linii i powstały już w r. Obecnie jest linii, które ciągle są wydłużane.
Tabela przedstawia zestawienie linii Wiedeńskiego Metra.
Linia | Trasa | Długość trasy | Liczba stacji |
U1 | Reumannplatz ↔ Leopoldau | ||
U2 | Seestadt ↔ Karlsplatz | ||
U3 | Ottakring ↔ Simmering | ||
U4 | Hütteldorf ↔ Heiligenstadt | ||
U6 | Siebenhirten ↔ Floridsdorf |
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Łączna długość linii Warszawskiego Metra wynosi .
- Pierwsza linia Warszawskiego Metra jest o krótsza od drugiej linii.
Przeciągnij i upuść.
, , ,
a) Jaka jest łączna długość dwóch najstarszych linii Wiedeńskiego Metra? ............
b) O ile kilometrów Warszawskie Metro jest krótsze od Wiedeńskiego Metra? ............
Wieża telewizyjna CN znajduje się w Toronto w Kanadzie. Ma ona wysokość . W niej na wysokości znajduje się obrotowa restauracja, wykonująca pełny obrót co minuty, zaś na wysokości umieszczono kawiarnię, w której jednorazowo może być gości. Panoramę Toronto możemy podziwiać w Sky Pad - galerii obserwacyjnej położonej na wysokości .
Fernsehturm to wieża telewizyjna stojąca w centrum Berlina. Pierwotna wysokość wieży wynosiła metrów, ale w roku zainstalowano nową antenę i obecnie wieża mierzy metrów. Wewnątrz kuli, na wysokości metra nad ziemią, znajduje się taras widokowy. Nad tarasem, na wysokości metra, położona jest restauracja z obrotowym pierścieniem, na którym umieszczone są stoliki. Obecnie pierścień dokonuje pełnego obrotu wokół osi w ciągu pół godziny (pierwotnie pełny obrót trwał pełną godzinę).
Przeciągnij i upuść.
, , ,
a) O ile metrów jest wyższa Wieża CN od wieży Fernsehturm? ..............
b) O ile metrów niżej położona jest obrotowa restauracja w Berlinie niż w Toronto? ..............
Rozstrzygnij, które zdanie jest prawdziwe, a które fałszywe.
- Taras widokowy w Toronto jest położony o wyżej niż taras widokowy w Berlinie.
- Restauracja na wieży CN wykonuje pełny obrót w czasie o minuty krótszym niż restauracja na wieży Fernsehturm.
Najdłuższy na świecie kolejowy tunel to Tunel Lötschberg w Szwajcarii o długości . Najdłuższym drogowym tunelem jest Tunel Lærdal w Norwegii. Ma on długość . Oblicz, o ile kilometrów jest dłuższy tunel kolejowy od drogowego?
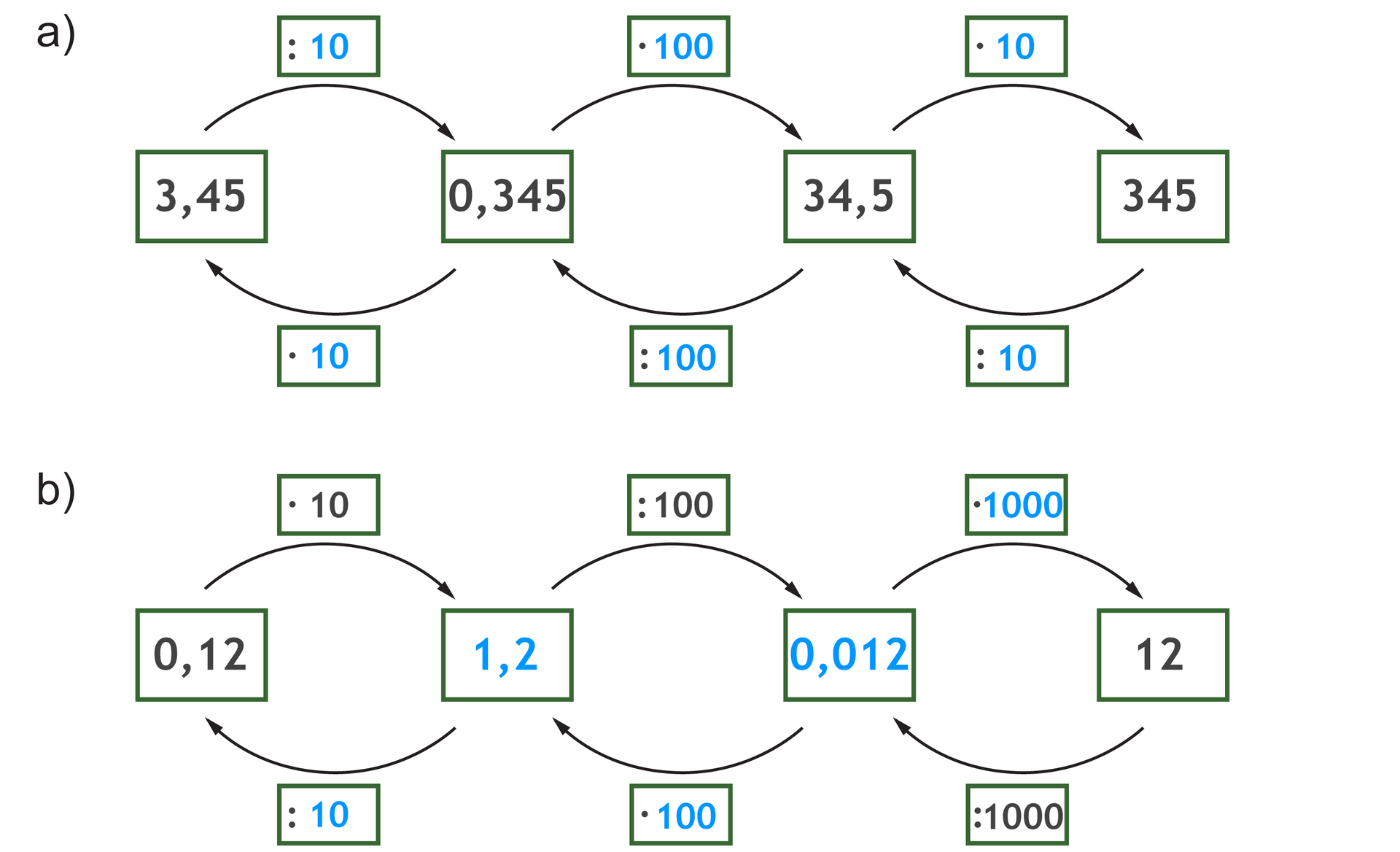
Mnożenie i dzielenie liczb dziesiętnych przez 10, 100, 1000,…
Mnożenie liczb dziesiętnych przez
Film dostępny na portalu epodreczniki.pl
Animacja
Mnożenie liczb dziesiętnych przez
Film dostępny na portalu epodreczniki.pl
Animacja
Mnożenie liczb dziesiętnych przez
Film dostępny na portalu epodreczniki.pl
Animacja
Dzieląc liczby dziesiętne przez , …, czasami musimy dopisać zera z lewej strony liczby lub opuścić niepotrzebne zera z jej prawej strony.

W tabeli podane są ceny biletów komunikacji miejskiej w Łodzi.
TARYFA MIEJSKA (Łódź) | ||
\* Bilety jedno‑przejazdowe (miejskie) | ulgowe | normalne |
Jednorazowy | ||
∗ Bilety czasowe (miejskie) | ||
minutowy | ||
minutowy | ||
minutowy | ||
Kasia kupiła dziesięć minutowych biletów ulgowych. Ile Kasia zapłaciła za bilety?
Rozstrzygnij, które zdanie jest prawdziwe, a które fałszywe.
- Dziesięć minutowych biletów normalnych kosztuje .
- Za złote kupimy dziesięć ulgowych biletów minutowych.
Uzupełnij
R1QKkReegVDep1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.RU4kC7SeNMHvC1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Aby pomnożyć liczbę dziesiętną przez , należy przesunąć w prawo przecinek odpowiednio o jedno, dwa, trzy, …, miejsca.
Aby podzielić liczbę dziesiętną przez ,…, należy przesunąć w lewo przecinek odpowiednio o jedno, dwa, trzy, …, miejsca.
Mnożenie i dzielenie liczb dziesiętnych
Dzielenie liczb dziesiętnych
Film dostępny na portalu epodreczniki.pl
Animacja
Film dostępny na portalu epodreczniki.pl
Animacja
Oblicz w pamięci.
Oblicz sposobem pisemnym.
Gdy mnożymy liczby dziesiętne, najpierw mnożymy liczby bez przecinków, a potem w wyniku oddzielamy przecinkiem tyle cyfr z prawej strony, ile było w obu czynnikach razem.

Wykorzystaj dane z rysunku i oblicz, ile trzeba zapłacić za
pomidorów
jabłek
cytryn
Państwo Kowalscy otrzymali powiadomienie o nowych miesięcznych opłatach za swoje mieszkanie o powierzchni . Oblicz, ile złotych miesięcznie państwo Kowalscy będą płacić za mieszkanie.
Koszty zarządu | |
Centralne ogrzewanie | |
Ciepła woda | |
Zimna woda i ścieki | |
Wywóz nieczystości |
Państwo Kowalscy chcą w pokoju położyć panele podłogowe. Podłoga ma wymiary . Panele podłogowe o klasie ścieralności mają grubość . Jedno opakowanie paneli podłogowych to . Metr kwadratowy paneli kosztuje .
Oblicz.
pole powierzchni, na której będą położone panele
ile co najmniej opakowań paneli trzeba kupić
ile złotych państwo Kowalscy zapłacą za panele, jeżeli kupią najmniejszą możliwą liczbę opakowań
Oblicz w pamięci.
Oblicz sposobem pisemnym.
Gdy dzielimy liczby dziesiętne, to przesuwamy przecinki w dzielnej i dzielniku o tyle samo miejsc, aby dzielnik był liczbą naturalną.
W ilorazie umieszczamy przecinek nad przecinkiem w dzielnej.
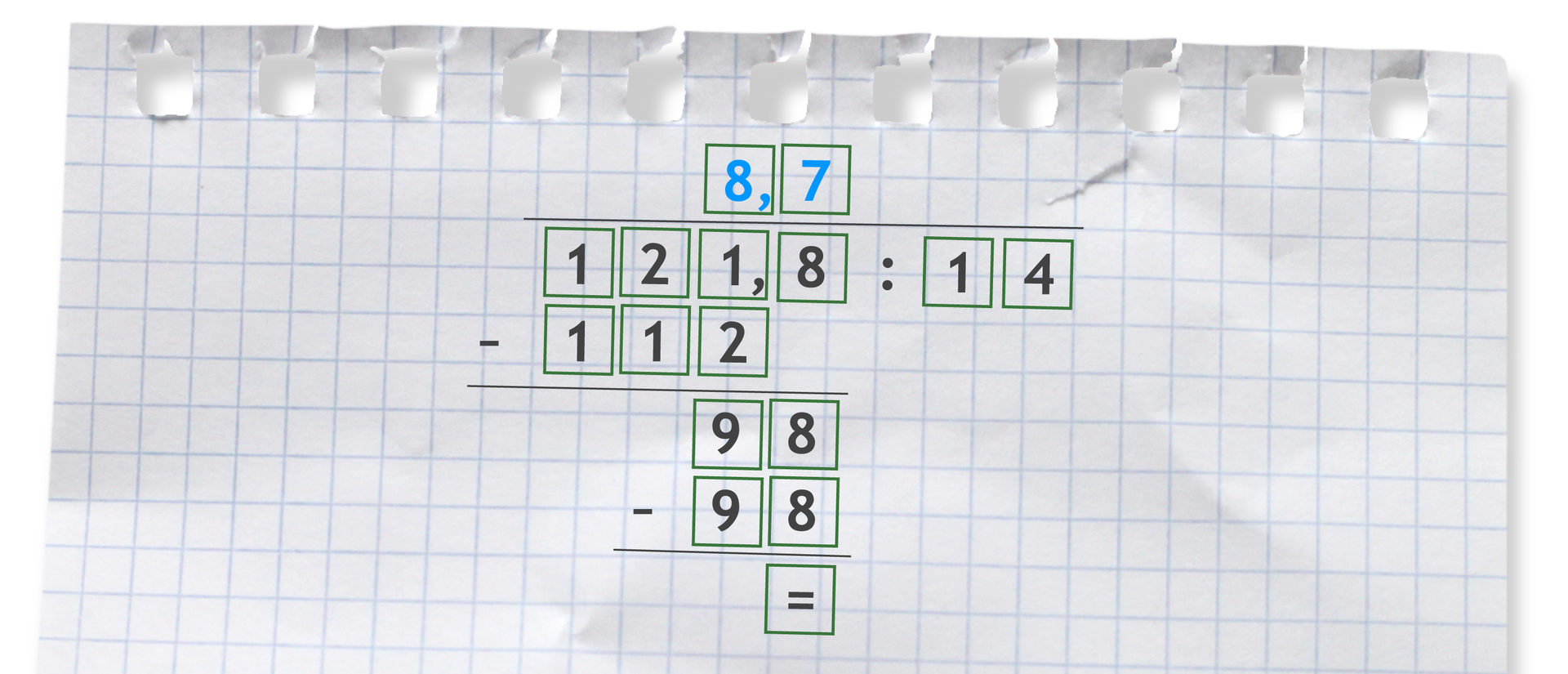
Odległość drogowa z Katowic do Gdańska wynosi , a na mapie wynosi ona. Oblicz, w jakiej skali sporządzona jest ta mapa.
Pani Kasia zapłaciła za 5 litra benzyny. Oblicz, ile złotych kosztuje litr tej benzyny.
W równoległoboku o polu jeden z boków ma długość . Jaką długość ma wysokość prostopadła do tego boku?
Łączenie działań na liczbach dziesiętnych
Film dostępny na portalu epodreczniki.pl
Animacja
Oblicz.
Wykonaj wskazane obliczenia.
Różnicę liczb i podziel przez sumę liczb i .
b) Sumę liczb i podziel przez różnicę liczb i .
Różnicę liczb i zwiększ razy.
Iloraz liczb i zmniejsz cztery razy.
Samolot leciał godzinę minut z prędkością , a następnie godziny z prędkością . Oblicz, ile kilometrów łącznie przeleciał ten samolot.