Działania na ułamkach zwykłych
Skracanie i rozszerzanie ułamków

Film dostępny na portalu epodreczniki.pl
Animacja
Dwa jednakowe kwadraty podzielono na równe części: jeden na , a drugi na części.

Uzupełnij.
Ponieważ jedna czwarta pierwszego kwadratu to taka sama część jak dwie ósme drugiego kwadratu, to
.
Uzupełnij brakujący licznik lub mianownik.
a) ............ b) ............
c) ............ d) ............
e) ............ f) ............
g) ............ h) ............
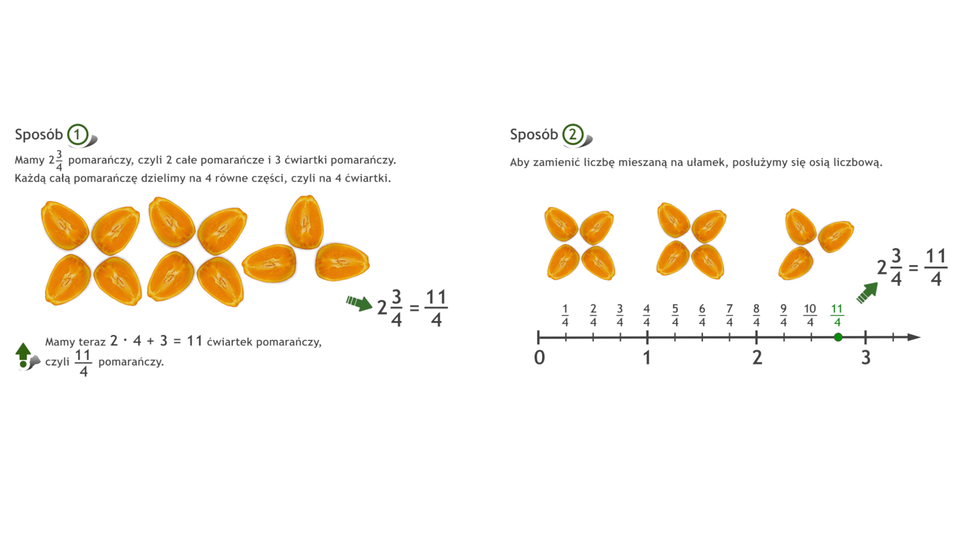
Liczby mieszane i ułamki niewłaściwe
Zamieniając liczbę mieszaną na ułamek trzeba tylko obliczyć licznik ułamka.
Łatwiejsze obliczenia wykonujemy w pamięci i zapisujemy zamianę krótko:
Film dostępny na portalu epodreczniki.pl
Animacja
Zamieniając ułamek niewłaściwy na liczbę mieszaną, wykorzystujemy wynik dzielenia licznika przez mianownik tego ułamka.
bo

Film dostępny na portalu epodreczniki.pl
Animacja
Przeciągnij i upuść.
, , , , , , ,
a) ............
b) ............
c) ............
d) ............
Przeciągnij i upuść.
, , , , , , ,
a) ............
b) ............
c) ............
d) ............
Wstaw brakujące liczby.
Dodawanie i odejmowanie ułamków zwykłych

Film dostępny na portalu epodreczniki.pl
Animacja
Wynikiem dodawania ułamków o tych samych mianownikach jest ułamek o tym samym mianowniku, którego licznik jest sumą liczników składników. Na przykład.

Film dostępny na portalu epodreczniki.pl
Animacja
Wynikiem odejmowania dwóch ułamków o tych samych mianownikach jest ułamek o tym samym mianowniku, którego licznik jest różnią licznika odjemnej i odjemnika.

Film dostępny na portalu epodreczniki.pl
Animacja
Aby dodać do siebie ułamki o różnych mianownikach, trzeba je najpierw sprowadzić do tego samego mianownika i postępować tak, jak w przykładzie .
Aby odjąć dwa ułamki o różnych mianownikach, trzeba je najpierw sprowadzić do tego samego mianownika i postępować tak, jak w przykładzie .
Staramy się, żeby wspólny mianownik ułamków był najmniejszą wspólną wielokrotnością mianowników.
wspólny mianownik jest iloczynem liczb i
to najmniejsza wspólna wielokrotność liczb i
wspólny mianownik to , bo jest podzielne przez
Oblicz. Wyniki wpisz w najprostszej postaci.
Przeciągnij i upuść.
, , , , , , ,
a) ............
b) ............
c) ............
d) ............
e) ............
f) ............
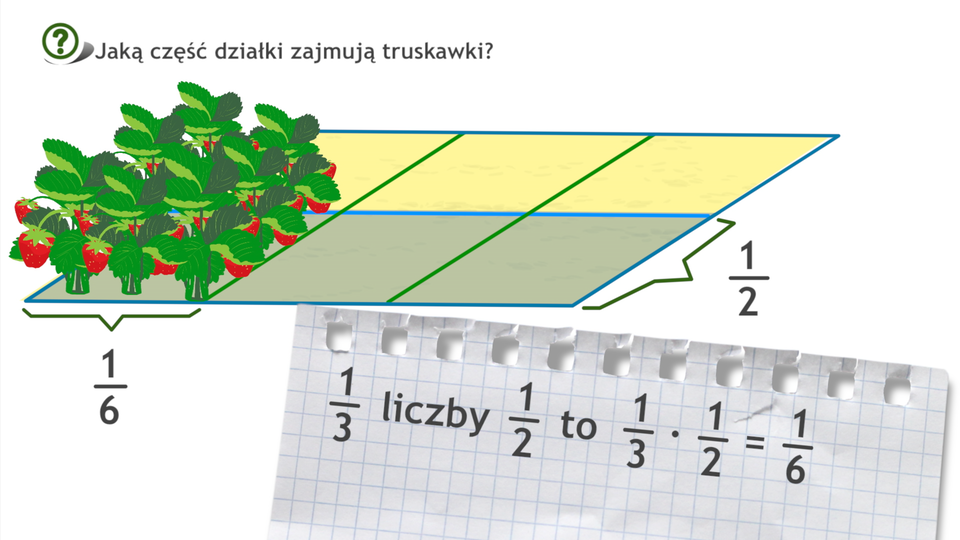
Mnożenie ułamków zwykłych
Film dostępny na portalu epodreczniki.pl
Animacja
Wynikiem mnożenia dwóch ułamków jest ułamek, którego licznik jest iloczynem liczników, a mianownik iloczynem mianowników mnożonych ułamków.
Jeżeli jeden z czynników jest liczbą mieszaną lub oba są liczbami mieszanymi, zamieniamy liczby mieszane na ułamki niewłaściwe.
Przeciągnij i upuść.
, , , , , , , , ,
a) ............ b) ............
c) ............ d) ............
e) ............ f) ............
g) ............ h) ............
Oblicz. Wyniki wpisz w najprostszej postaci.
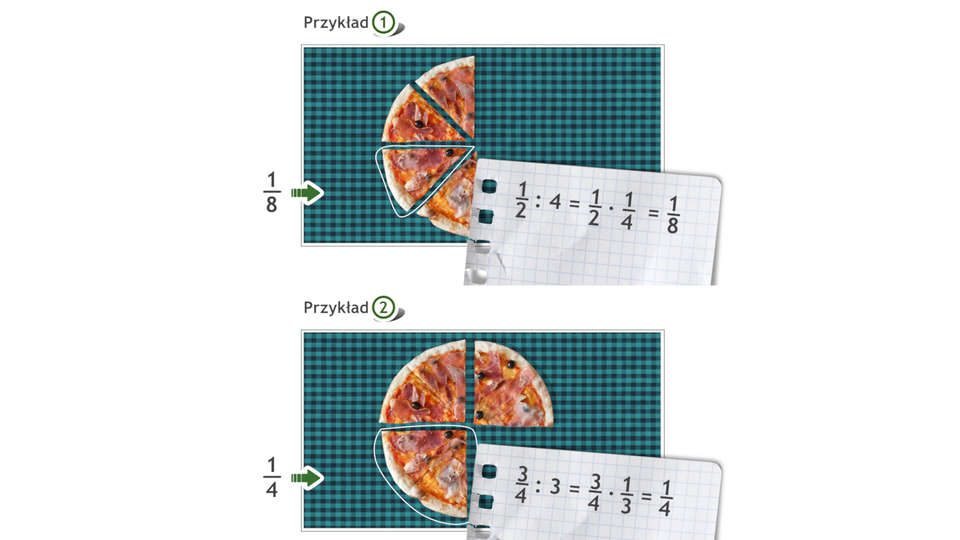
Dzielenie ułamków zwykłych
Film dostępny na portalu epodreczniki.pl
Animacja
Dzieląc ułamek przez liczbę naturalną wystarczy pomnożyć tę liczbę przez mianownik ułamka, a licznik pozostawić ten sam.
Aby podzielić dwa ułamki zwykłe, mnożymy pierwszy z tych ułamków przez odwrotność drugiego.
Jeżeli dzielna lub dzielnik są liczbami mieszanymi, zanim wykonamy dzielenie, zamieniamy liczby mieszane na ułamki niewłaściwe.
W pewnych sytuacjach, dzieląc ułamki zwykłe warto dzielić licznik dzielnej przez licznik dzielnika, a mianownik dzielnej przez mianownik dzielnika. Na przykład:
Przeciągnij i upuść.
, , , , , , , , ,
a) ............ b) ............
c) ............ d) ............
e) ............ f) ............
g) ............ h) ............
i) ............ j) ............
Oblicz. Wyniki wpisz w najprostszej postaci.
Oblicz. Wyniki wpisz w najprostszej postaci.
Mnożenie i dzielenie ułamków zwykłych
Przeciągnij i upuść.
, , , , , , ,
a) ............ b) ............
c) ............ d) ............
e) ............ f) ............
g) ............ h) ............
Przeciągnij i upuść.
, , , ,
a) ............
b) ............
c) ............
Przeciągnij i upuść.
, , , ,
a) ............
b) ............
c) ............
Łączenie działań na ułamkach zwykłych

Film dostępny na portalu epodreczniki.pl
Animacja
Przeciągnij i upuść.
, , , , ,
a) ............
b) ............
c) ............
d) ............
e) ............
f) ............
Oblicz.
Oblicz tak, jak w przykładach.
Przykłady
Przeciągnij i upuść.
, , ,
a) ............
b) ............
c) ............
d) ............
Obliczanie ułamka danej liczby
Aby obliczyć ułamek danej liczby (lub ułamek z danej liczby), należy pomnożyć ułamek przez tę liczbę. Na przykład: liczby wynosi , ponieważ .
Oblicz w pamięci.
z
z
z
z
ze
z
ze
z
Przeciągnij i upuść.
, , , ,
a) Wujek Henryk zjadł swego urodzinowego tortu ważącego . Ile kilogramów tortu pozostaje dla gości wujka Henryka?
Odpowiedź: Dla gości pozostaje ............ tortu.
b) Kacper ma złotych, a Beata tej kwoty. O ile złotych mniej ma Beata?
Odpowiedź: Beata ma mniej o ............ zł.
c) W sklepie „Wszystko po ” Brunon kupił przedmiotów. Rozdał kolegom zakupionych rzeczy. Ile kosztowały prezenty podarowane przez Brunona kolegom?
Odpowiedź: Prezenty kosztowały ............ zł.
Wybierz wyrażenie opisujące następującą sytuację:
Tomek przespał czwartą część doby, jedną dziewiątą reszty doby spędził na odrabianiu pracy domowej. Ile czasu Tomek spędził na odrabianiu pracy domowej?
Tomek przespał czwartą część doby, jedną dziewiątą reszty doby spędził na odrabianiu pracy domowej. Jaką część doby Tomek nie spał i nie odrabiał pracy domowej?