Dzielenie przez ułamek

Uczyliśmy się już dzielić ułamek przez liczbę naturalną. Ale jak podzielić liczbę naturalną przez ułamek? Albo ułamek przez ułamek?
Jak wykonać dzielenia typu: $1 : \frac{1}{4}$ czy $\frac{5}{6} : \frac{1}{3}$ ?
Przyjrzyjmy się poniższym zadaniom.

Ćwiczenie 1

Wstaw w licznik i mianownik ułamka jak najmniejsze liczby tak, by otrzymany iloczyn był zawsze równy $1$ .

$\frac{2}{5} ∙ \frac{\dots}{\dots} = 1$
$\frac{3}{4} ∙ \frac{\dots}{\dots} = 1$
$\frac{3}{8} ∙ \frac{\dots}{\dots} = 1$
$1 \frac{1}{6} ∙ \frac{\dots}{\dots} = 1$
$2 \frac{7}{9} ∙ \frac{\dots}{\dots} = 1$
$3 \frac{3}{8} ∙ \frac{\dots}{\dots} = 1$
$7 ∙ \frac{\dots}{\dots} = 1$
$8 ∙ \frac{\dots}{\dots} = 1$
$3 ∙ \frac{\dots}{\dots} = 1$

$\frac{5}{2}$
$\frac{4}{3}$
$\frac{8}{3}$
$\frac{6}{7}$
$\frac{9}{25}$
$\frac{8}{27}$
$\frac{1}{7}$
$\frac{1}{8}$
$\frac{1}{3}$

Odwrotność liczby

Definicja: Odwrotność liczby

Jeśli iloczyn dwóch liczb różnych od zera jest równy $1$ , to każda z tych liczb jest odwrotnością tej drugiej.
Na przykład odwrotnościami są liczby
$\frac{2}{5}$ i $\frac{5}{2}$ , $5$ i $\frac{1}{5}$ , $2 \frac{2}{7}$ i $\frac{7}{16}$

R8cbPVk0KvI3B1

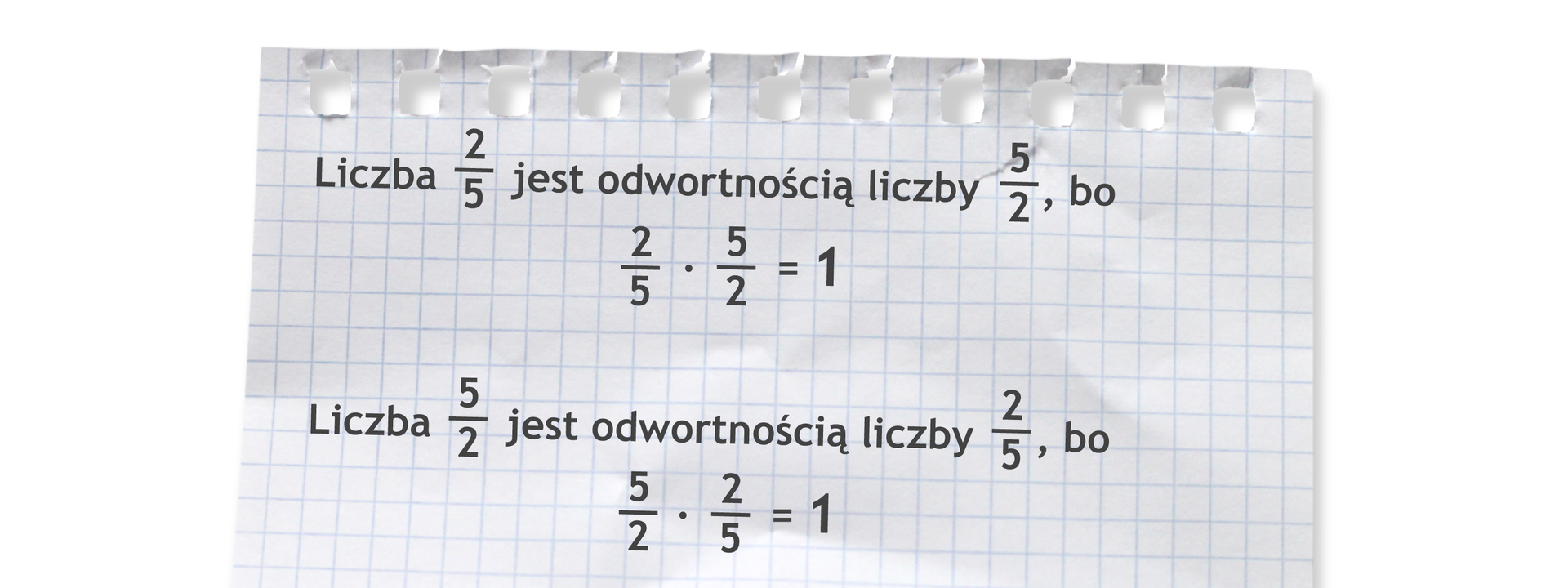
Dwa przykłady. Pierwszy: Liczba dwie piąte jest odwrotnością liczby pięć drugich, bo dwie piąte razy pięć drugich =1. Drugi: Liczba pięć drugich jest odwrotnością liczby dwie piąte, bo pięć drugich razy dwie piąte =1.

Ćwiczenie 2

R1BddYWGgiqwe1

Wybierz.

2, ma odwrotność, 1, nie ma odwrotności, 3, 0

Liczba 0 .......................................
Odwrotnością liczby jeden jest liczba .......................................

Ćwiczenie 3

Uzupełnij tabelę. Liczby zapisz w postaci ułamka zwykłego lub liczby naturalnej.

Tabela. Dane
Liczba	Odwrotność liczby
$\frac{2}{3}$
$\frac{4}{5}$
	$\frac{6}{7}$
	$\frac{9}{15}$
	$3$
$7$
	$9$

Tabela. Dane
Liczba	Odwrotność liczby
$\frac{2}{3}$	$\frac{3}{2}$
$\frac{4}{5}$	$\frac{5}{4}$
$\frac{7}{6}$	$\frac{6}{7}$
$\frac{15}{9}$	$\frac{9}{15}$
$\frac{1}{3}$	$3$
$7$	$\frac{1}{7}$
$\frac{1}{9}$	$9$

Ćwiczenie 4

R1C5RkP5e5BLu1

Wyznacz odwrotności następujących liczb mieszanych, a następnie przeciągnij i upuść.

$\frac{2}{25}$ , $\frac{4}{23}$ , $\frac{3}{4}$ , $\frac{5}{12}$ , $\frac{7}{83}$ , $\frac{9}{75}$

a) $1 \frac{1}{3}$ ............
b) $2 \frac{2}{5}$ ............
c) $5 \frac{3}{4}$ ............
d) $12 \frac{1}{2}$ ............
e) $11 \frac{6}{7}$ ............
f) $8 \frac{3}{9}$ ............

Dzielenie liczb naturalnych przez ułamki

Ćwiczenie 5

Uzupełnij obliczenia, a następnie zdanie poniżej.

$1 : \frac{1}{4} = 4$ lub $1 ∙ \dots = \dots$
$3 : \frac{1}{4} = \dots$ lub $3 ∙ \dots = \dots$
$1 : \frac{2}{3} = \dots$ lub $1 ∙ \frac{3}{2} = \dots$
$2 : 1 \frac{1}{2} = \dots$ lub $2 ∙ \frac{2}{3} = \dots$
Dzielenie przez ułamek zwykły można zastąpić ... przez … tego ułamka.

$4, 4$
$12, 4, 12$
$\frac{3}{2}, \frac{3}{2}$
$\frac{4}{3}, \frac{4}{3}$
mnożeniem, odwrotność

Ważne!

Aby podzielić liczbę naturalną przez ułamek, należy ją pomnożyć przez odwrotność tego ułamka.

Rzpo2SDAD84Kf1

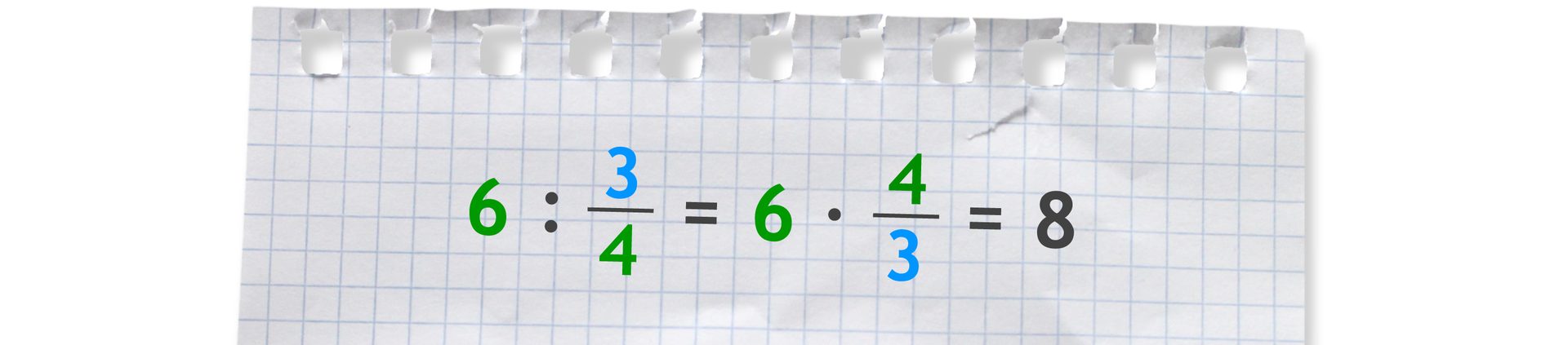
Przykład: 6 dzielone przez trzy czwarte równa się 6 razy cztery trzecie =8.

Ćwiczenie 6

R1UzDt3dNAOYn1

W dzbanku znajdowały się dwa litry soku. Kasia rozlała go po równo do szklaneczek o pojemności $\frac{1}{5}$ litra. Ile porcji soku otrzymała?

Odp.: Kasia otrzymała ............ porcji soku.

Ćwiczenie 7

Rr8xmWEWXMlBm1

Tomek $15 kg$ borówek amerykańskich rozdzielił po równo do pudełek. W jednym pudełku mieści się $\frac{1}{4} kg$ borówek. Ile pudełek z borówkami miał Tomek?

Odp.: Tomek miał ............ pudełek z borówkami.

iGwqGXZUDF_d5e349

Ćwiczenie 8

Krok dorosłego człowieka ma przeciętnie $\frac{3}{4} m$ długości. Ile kroków musi przejść dorosły, aby przebyć $150 m$ ?

$200$

Ćwiczenie 9

R1Di1YqAi570j1

Ważne!

Aby podzielić liczbę naturalną przez liczbę mieszaną, należy najpierw zamienić liczbę mieszaną na ułamek niewłaściwy, a potem wykonać dzielenie liczby naturalnej przez ułamek.
Na przykład:

RWwXHOcNbtD591

Przykład: 6 dzielone przez jeden i jedna druga równa się 6 dzielone przez trzy drugie równa się 6 razy dwie trzecie =4.

Ćwiczenie 10

Oblicz. Wynik zapisz w najprostszej postaci.

$33 : 1 \frac{5}{6}$
$36 : 2 \frac{2}{5}$
$18 : 1 \frac{1}{3}$
$14 : 1 \frac{2}{3}$
$2 : 2 \frac{1}{4}$
$3 : 4 \frac{2}{7}$

$18$
$15$
$13 \frac{1}{2}$
$8 \frac{2}{5}$
$\frac{8}{9}$
$\frac{7}{10}$

Dzielenie ułamków zwykłych

Przykład 1

Uzasadniliśmy, że $\frac{5}{6} : \frac{1}{3} = 2 \frac{1}{2}$ .
Sprawdźmy, czy otrzymamy ten sam wynik, mnożąc $\frac{5}{6}$ przez odwrotność ułamka $\frac{1}{3}$ , czyli przez $3$ .

\frac{5}{6} ∙ 3 = \frac{5}{2} = 2 \frac{1}{2}

iGwqGXZUDF_d5e470

Ważne!

Aby podzielić ułamek zwykły przez ułamek zwykły, należy pierwszy ułamek pomnożyć przez odwrotność drugiego.
Na przykład:

RWjjAJIpW9EUv1

Przykład: siedem dziewiątych dzielone przez czternaście trzecich równa się siedem dziewiątych razy trzy czternaste równa się jedna szósta.

Ćwiczenie 11

Oblicz.

$\frac{2}{3} : \frac{3}{2}$
$\frac{7}{8} : \frac{4}{5}$
$\frac{3}{7} : \frac{4}{5}$
$\frac{5}{7} : \frac{1}{13}$
$\frac{7}{9} : \frac{5}{18}$
$\frac{8}{11} : \frac{4}{33}$
$\frac{9}{10} : \frac{3}{2}$
$\frac{5}{14} : \frac{2}{7}$
$\frac{2}{3} : \frac{5}{24}$

$\frac{4}{9}$
$1 \frac{3}{32}$
$\frac{15}{28}$
$9 \frac{2}{7}$
$2 \frac{4}{5}$
$6$
$\frac{3}{5}$
$1 \frac{1}{4}$
$3 \frac{1}{5}$

Ćwiczenie 12

RfzoMySEf54I31

Przykład 2

$5 \frac{1}{4}$ litra soku rozlano do butelek o pojemności $1 \frac{1}{4}$ litra. Obliczmy, ile butelek wykorzystano i jaką część ostatniej butelki zajmie sok.

$1$ butelka - $1 \frac{1}{4}$ litra
$2$ butelki - $2 \frac{2}{4}$ litra
$3$ butelki - $3 \frac{3}{4}$ litra
$4$ butelki - $5$ litrów za mało
$5$ butelek - $6 \frac{1}{4}$ litra za dużo

Wykorzystano $5$ butelek, ale w piątej była tylko $\frac{1}{4}$ litra soku, a to jest $\frac{1}{5}$ część pojemności butelki.
Wykonaliśmy dzielenie:

5 \frac{1}{4} : 1 \frac{1}{4} = 4 \frac{1}{5}

RGZSLaKDnOxE11

Dzielenie ulamkow zwyklych_atrapa_animacja_428

Ćwiczenie 13

Uzupełnij obliczenia. Pamiętaj o skracaniu ułamków.

$16 \frac{2}{3} : 2 \frac{2}{9} = \frac{\dots}{\dots} : \frac{20}{9} = \frac{\dots}{\dots} ∙ \frac{9}{20} = 7 \frac{\dots}{\dots}$
$1 \frac{3}{7} : 2 \frac{4}{7} = \frac{10}{7} : \frac{}{} = \frac{\dots}{\dots} ∙ \frac{\dots}{\dots} = \frac{\dots}{\dots}$
$15 \frac{3}{4} : 2 \frac{1}{4} = \frac{\dots}{\dots} : \frac{9}{4} = \frac{\dots}{\dots} ∙ \frac{\dots}{\dots} = \dots$
$4 \frac{2}{7} : 1 \frac{2}{3} = \frac{30}{7} : \frac{\dots}{\dots} = \frac{30}{7} ∙ \frac{\dots}{\dots} = \dots \frac{\dots}{\dots}$
$3 \frac{1}{8} : 6 \frac{2}{3} = \frac{\dots}{\dots} : \frac{20}{3} = \frac{\dots}{\dots} ∙ \frac{\dots}{\dots} = \frac{\dots}{\dots}$
$3 \frac{9}{11} : 1 \frac{13}{22} = \frac{42}{11} : \frac{}{} = \frac{42}{11} ∙ \frac{}{} = \dots \frac{}{}$

$16 \frac{2}{3} : 2 \frac{2}{9} = \frac{50}{3} : \frac{20}{9} = \frac{50}{3} ∙ \frac{9}{20} = 7 \frac{1}{2}$
$1 \frac{3}{7} : 2 \frac{4}{7} = \frac{10}{7} : \frac{18}{7} = \frac{10}{7} ∙ \frac{7}{18} = \frac{5}{9}$
$15 \frac{3}{4} : 2 \frac{1}{4} = \frac{63}{4} : \frac{9}{4} = \frac{63}{4} ∙ \frac{4}{9} = 7$
$4 \frac{2}{7} : 1 \frac{2}{3} = \frac{30}{7} : \frac{5}{3} = \frac{30}{7} ∙ \frac{3}{5} = 2 \frac{4}{7}$
$3 \frac{1}{8} : 6 \frac{2}{3} = \frac{25}{8} : \frac{20}{3} = \frac{25}{8} ∙ \frac{3}{20} = \frac{15}{32}$
$3 \frac{9}{11} : 1 \frac{13}{22} = \frac{42}{11} : \frac{35}{22} = \frac{42}{11} ∙ \frac{22}{35} = 2 \frac{2}{5}$

Ćwiczenie 14

R1LaHTD9ydD5g1

Kilogram borówek amerykańskich kosztuje $12 \frac{3}{4} zł$ . Ile kilogramów borówek można kupić za $15 \frac{3}{10} zł$ ?

$1 \frac{1}{5}$ , $\frac{1}{7}$ , $\frac{1}{8}$ , $1 \frac{1}{7}$

Odp. : Można kupić ............ $kg$ borówek amerykańskich.

Ćwiczenie 15

Znajdź liczbę $1 \frac{1}{8}$ razy mniejszą od różnicy odwrotności liczb $\frac{1}{7}$ i $2 \frac{1}{5}$ .

$5 \frac{9}{11}$

Ćwiczenie 16

Oblicz.

$\frac{9 \frac{1}{3}}{16 : \frac{8}{14}}$
$\frac{4 \frac{4}{15} : \frac{16}{25}}{5 \frac{2}{6} : \frac{16}{36}}$
$\frac{5 \frac{1}{2} : \frac{11}{16}}{8 \frac{7}{10} : 11 \frac{3}{5}}$

$\frac{1}{3}$
$\frac{5}{9}$
$10 \frac{2}{3}$

Dzielenie ułamków przez liczby naturalne

Działania na ułamkach zwykłych

Dzielenie ułamków zwykłych

Dzielenie przez ułamek

Dzielenie liczb naturalnych przez ułamki

Dzielenie ułamków zwykłych