Galeria zdjęć interaktywnych
Przeanalizuj galerię zdjęć interaktywnych i zapoznaj się ze sposobem rozwiązania zadania i wyboru liczb, które są rozwiązaniami zadania.


1. {audio}Najpierw skorzystamy z wniosku z twierdzenia Pitagorasa.


1. {audio}Wprowadzimy oznaczenia boków trójkąta rozwartokątnego.
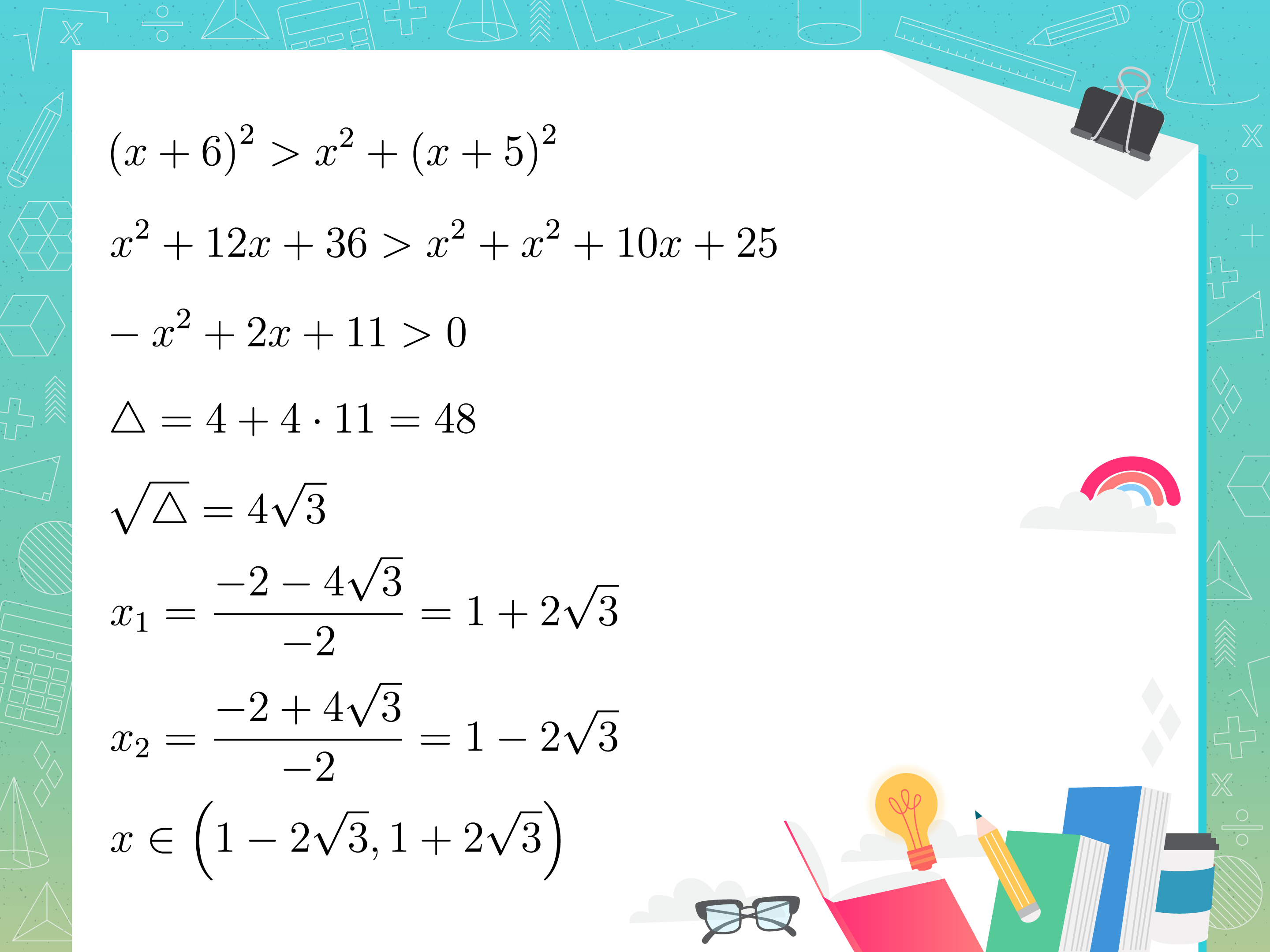
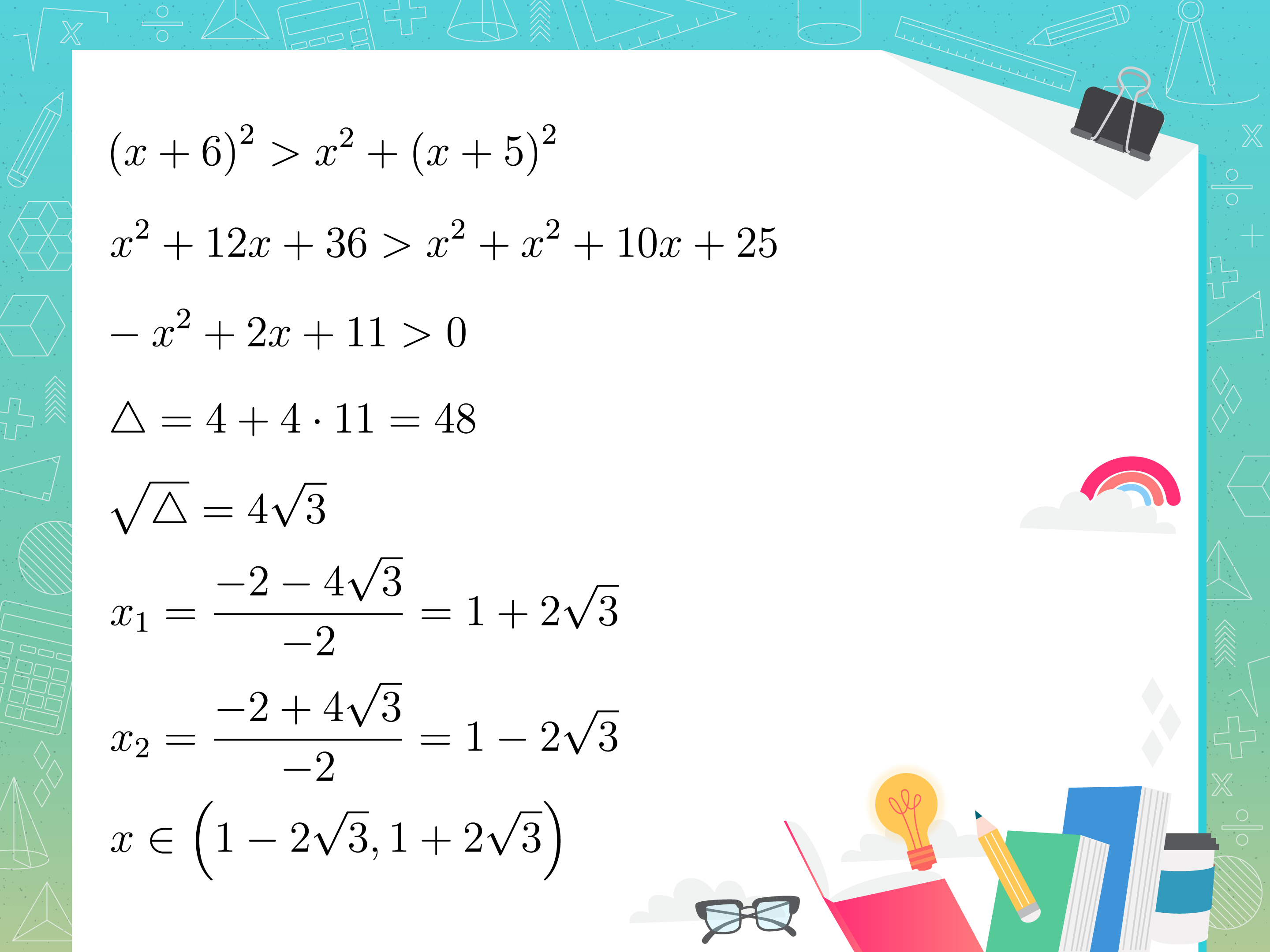
1. {audio}Zapiszemy i rozwiążemy nierówność opisującą sytuację przedstawioną w zadaniu.


1. {audio}Ponieważ boki trójkąta mają być liczbami naturalnymi jednocyfrowymi, więc może być równy , , lub .





1. {audio}Rozpatrzymy teraz możliwe „trójki” boków trójkąta.
2. {audio}Dla odcinków długości , , nie jest spełniona nierówność trójkąta.
3. {audio}Boki trójkąta mają być liczbami jednocyfrowymi, a nie jest taką liczbą. Trójkąt nie spełnia warunków zadania.
4. {audio}Warunki zadania spełniają dwie „trójki” liczb.
Różnica długości krótszych boków w trójkącie rozwartokątnym jest równa . Najdłuższy bok trójkąta jest o dłuższy od najkrótszego boku. Oblicz możliwe długości boków tego trójkąta, jeżeli wiadomo, że wyrażają się one liczbami jednocyfrowymi.
Jeżeli , , są bokami w trójkącie i jest najdłuższym bokiem, to aby trójkąt był rozwartokątny musi być spełniony warunek .
, , lub , , .