Galeria zdjęć interaktywnych
Zapoznaj się z przykładem przedstawionym w galerii zdjęć interaktywnych, a następnie wykonaj polecenie 2 i 3.






1. {audio}Przedstawmy licznik i mianownik ułamka algebraicznego w postaci iloczynowej.
2. {audio}Po skróceniu wyrażenia przez , otrzymujemy wartość bezwzględną różnicy ilorazu , oraz większą od .
3. {audio}Sprowadźmy ułamki algebraiczne do wspólnego mianownika.
4. {audio}Zapiszmy lewą stronę nierówności za pomocą jednej kreski ułamkowej.
5. {audio}Otrzymujemy dwie nierówności wymierne.
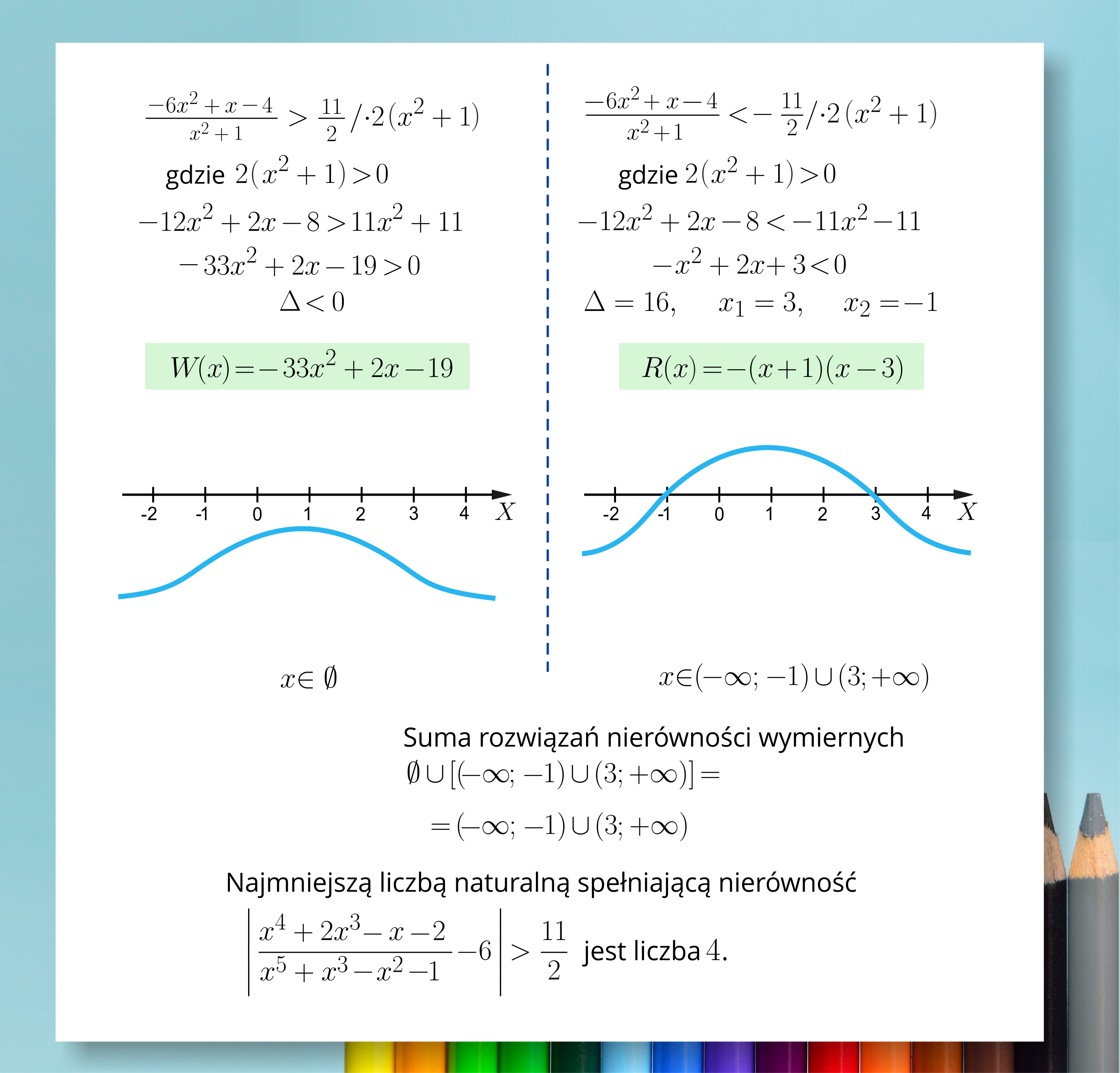
W danym przypadku nie mnożymy przez kwadrat mianownika, ponieważ dla : . Przypadek pierwszy, , gdzie . Zwrot nierówności nie ulega zmianie, ponieważ mnożymy nierówność obustronnie przez . Doprowadzamy nierówność do najprostszej postaci. , . Wyróżnik trójmianu kwadratowego jest ujemny. Delta mniejsza od zera. . Sporządzamy wykres funkcji wielomianowej . Ilustracja przedstawia poziomą oś X od minus dwóch do czterech oraz wykres funkcji znajdujący się całkowicie pod osią X. Brak rozwiązań. Przypadek drugi. . Nierówność mnożymy obustronnie przez .
W danym przypadku nie mnożymy przez kwadrat mianownika, ponieważ dla : . Gdzie . Zwrot nierówności nie ulega zmianie, ponieważ mnożymy nierówność obustronnie przez . Doprowadzamy nierówność do najprostszej postaci. , . Wyróżnik trójmianu kwadratowego jest dodatni. . . Sporządzamy wykres funkcji wielomianowej . Ilustracja przedstawia poziomą oś X od minus dwóch do czterech oraz wykres funkcji, parabolę z ramionami skierowanymi w dół. Wykres przyjmuje wartości dodanie w przedziale oraz wartości ujemne w przedziale . . Najmniejszą liczbą naturalną spełniającą nierówność jest liczba cztery.
W danym przypadku nie mnożymy przez kwadrat mianownika, ponieważ dla : . Przypadek pierwszy, , gdzie . Zwrot nierówności nie ulega zmianie, ponieważ mnożymy nierówność obustronnie przez . Doprowadzamy nierówność do najprostszej postaci. , . Wyróżnik trójmianu kwadratowego jest ujemny. Delta mniejsza od zera. . Sporządzamy wykres funkcji wielomianowej . Ilustracja przedstawia poziomą oś X od minus dwóch do czterech oraz wykres funkcji znajdujący się całkowicie pod osią X. Brak rozwiązań. Przypadek drugi. . Nierówność mnożymy obustronnie przez .
W danym przypadku nie mnożymy przez kwadrat mianownika, ponieważ dla : . Gdzie . Zwrot nierówności nie ulega zmianie, ponieważ mnożymy nierówność obustronnie przez . Doprowadzamy nierówność do najprostszej postaci. , . Wyróżnik trójmianu kwadratowego jest dodatni. . . Sporządzamy wykres funkcji wielomianowej . Ilustracja przedstawia poziomą oś X od minus dwóch do czterech oraz wykres funkcji, parabolę z ramionami skierowanymi w dół. Wykres przyjmuje wartości dodanie w przedziale oraz wartości ujemne w przedziale . . Najmniejszą liczbą naturalną spełniającą nierówność jest liczba cztery.







1. {audio}Nierówność mnożymy obustronnie przez .
W danym przypadku nie mnożymy przez kwadrat mianownika, ponieważ dla : .
2. {audio}Zwrot nierówności nie ulega zmianie, ponieważ mnożymy nierówność obustronnie przez .
3. {audio}Doprowadzamy nierówność do najprostszej postaci.
4. {audio}Wyróżnik trójmianu kwadratowego jest ujemny.
5. {audio}Wyróżnik trójmianu kwadratowego jest dodatni.
6. {audio}Sporządzamy wykres funkcji wielomianowej .
7. {audio}Sporządzamy wykres funkcji wielomianowej .
Oblicz największą liczbę naturalną spełniającą nierówność .
Zakoduj cyfry: setek, dziesiątek, jedności liczby
............
Suma liczb naturalnych spełniających nierówność wynosi