• $\frac{W_1\left(x\right)}{W_2\left(x\right)}>0 \iff W_1\left(x\right)·W_2\left(x\right)>0 \wedge W_2\left(x\right)\ne 0$

• $\frac{W_1\left(x\right)}{W_2\left(x\right)}<0 \iff W_1\left(x\right)·W_2\left(x\right)<0 \wedge W_2\left(x\right)\ne 0$

• $\frac{W_1\left(x\right)}{W_2\left(x\right)}\ge 0 \iff W_1\left(x\right)·W_2\left(x\right)\ge 0 \wedge W_2\left(x\right)\ne 0$

• $\frac{W_1\left(x\right)}{W_2\left(x\right)}\le 0 \iff W_1\left(x\right)·W_2\left(x\right)\le 0 \wedge W_2\left(x\right)\ne 0$

Wyznaczymy dziedzinę funkcji postaci $f\left(x\right)=\sqrt{\frac{{\displaystyle x^3+3x^2-3x-9}}{{\displaystyle x^2-2x+1}}}$.

Rozwiązanie

Z własności pierwiastka wiadomo, że wyrażenie pod pierwiastkiem  musi być nieujemne. Zatem wyznaczenie dziedziny podanej funkcji sprowadzi się do rozwiązania nierówności postaci $\frac{{\displaystyle x^3+3x^2-3x-9}}{{\displaystyle x^2-2x+1}}\ge 0$.

Skorzystajmy z twierdzenia o równoważności nierówności i zapiszemy nierowność według wzoru

$\frac{W_1\left(x\right)}{W_2\left(x\right)}\ge 0 \iff W_1\left(x\right)·W_2\left(x\right)\ge 0 \wedge W_2\left(x\right)\ne 0$.

Zaczniemy od założenia $W_2\left(x\right)\ne 0$. Zatem

$x^2-2x+1\ne 0$,

${\left(x-1\right)}^2\ne 0$,

$\left(x-1\right)\ne 0$,

$x\ne 1$.

Przejdziemy teraz do warunku $W_1\left(x\right)·W_2\left(x\right)\ge 0$.

Zapiszmy w takim razie licznik i mianownik ułamka algebraicznego $\frac{x^3+3x^2-3x-9}{x^2-2x+1}$ w postaci iloczynowej stosując metodę grupowania wyrazów oraz wzory skróconego mnożenia

$\frac{x^3+3x^2-3x-9}{x^2-2x+1}\ge 0$,

$\frac{{\displaystyle x^2\left(x+3\right)-3\left(x+3\right)}}{{\displaystyle \left(x-1\right){}^2}}\ge 0$,

$\frac{{\displaystyle \left(x^2-3\right)\left(x+3\right)}}{{\displaystyle \left(x-1\right){}^2}}\ge 0$.

$\left(x^2-3\right)\left(x+3\right){\left(x-1\right)}^2\ge 0$,

$\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\left(x+3\right){\left(x-1\right)}^2\ge 0$.

Wielomian $W\left(x\right)=\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\left(x+3\right){\left(x-1\right)}^2$ ma trzy pierwiastki jednokrotne: $\left(-\sqrt{3}\right)$, $\left(-3\right)$ oraz $\sqrt{3}$ i jeden pierwiastek podwójny równy $1$. Pamiętajmy, że z pierwszego sprawdzanego warunku $1$ nie może być rozwiązaniem.

Uwzględniając założenie $x\ne 1$ wykres rozwiązań jest postaci

R1StD68NeyPN2

Ilustracja przedstawia poziomą oś X oraz wykres funkcji przyjmujący wartości dodanie w przedziale $<-3;-\sqrt{3}>\cup <\sqrt{3};\infty )$ oraz wartości ujemne w przedziale $(-\sqrt{3};\sqrt{3})$. W punkcie jeden wykres odbija się od osi X.

Odpowiedź: Dziedziną rozważanej funkcji  jest zbiór $⟨-3,-\sqrt{3}⟩\cup \left.⟨\sqrt{3},\infty \right)$.

Ile liczb  całkowitych należy do zbioru rozwiązań  nierówności $\frac{x^4-x^3+8x-8}{2x^3-4x^2-6x+12}\le 0$?

Rozwiązanie

Podajmy konieczne założenie $2x^3-4x^2-6x+12\ne 0$,

$2x^2\left(x-2\right)-6\left(x-2\right) \ne 0$,

$2\left(x^2-3\right)\left(x-2\right) \ne 0$,

$x^2-3\ne 0$, $x-2 \ne 0$

$x^2\ne 3$, $x\ne 2$

$x\ne -\sqrt{3}$, $x\ne \sqrt{3}$,$x\ne 2$.

Zatem $D=\mathrm{ℝ}\setminus \left\{-\sqrt{3};\sqrt{3};2\right\}$.

Zapiszmy licznik i mianownik ułamka algebraicznego $\frac{x^5-x^4+8x-8}{2x^3-4x^2-6x+12}$ w postaci iloczynowej stosując metodę grupowania wyrazów

$\frac{x^3\left(x-1\right)+8\left(x-1\right)}{2x^2\left(x-2\right)-6\left(x-2\right)}\le 0$,

$\frac{\left(x^3+8\right)\left(x-1\right)}{2\left(x^2-3\right)\left(x-2\right)}\le 0$,

$\frac{\left(x^4+8\right)\left(x-1\right)}{2\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\left(x-2\right)}\le 0$.

Zauważmy, że mianownik mogliśmy zapisać od razu w postaci iloczynowej po obliczeniu dziedziny.

Skorzystajmy z twierdzenia i zapiszmy nierówność wymierną jako równoważną nierówność wielomianową przy wyznaczonej dziedzinie nierówności wymiernej

$\frac{W_1\left(x\right)}{W_2\left(x\right)}\le 0\iff W_1\left(x\right)\cdot W_2\left(x\right)\le 0\wedge W_2\left(x\right)\ne 0$,

$\frac{\left(x^3+8\right)\left(x-1\right)}{2\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\left(x-2\right)}\le 0\iff 2\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\left(x-2\right)\left(x^3+8\right)\left(x-1\right)\le 0$$\wedge x\ne -\sqrt{3}$, $x\ne \sqrt{3}$, $x\ne 2$.

Wielomian 
$W\left(x\right)=2\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\left(x-2\right)\left(x^3+8\right)\left(x-1\right)$ ma pięć pierwiastków: $\left(-2\right)$; $\left(-\sqrt{3}\right)$; $1$; $\sqrt{3}$; $2$.

Uwzględniając dziedzinę nierówności wymiernej $D=\mathrm{ℝ}\setminus \left\{-\sqrt{3};\sqrt{3};2\right\}$ rysujemy szkic wykresu.

RBzHPtb7HltEI

Ilustracja przedstawia poziomą oś X oraz wykres funkcji przyjmujący wartości dodanie w przedziale $<-2;-\sqrt{3})\cup <1;\sqrt{3})\cup (2;\infty )$ oraz wartości ujemne w przedziale $(-\infty ;2)\cup (-\sqrt{3};1)\cup (\sqrt{3};2)$.

Odpowiedź: Do zbioru rozwiązań nierówności należy  nieskończenie wiele liczb całkowitych. Np.   $x=1$,  $x=0$.

Rozwiążemy nierówność $\frac{7x^3+2x^2-21x-6}{9x^3-4x^2-27x+12}\ge 0$.

Rozwiązanie

Podajmy konieczne założenie $9x^3-4x^2-27x+12\ne 0$,

$x^2\left(9x-4\right)-3\left(9x-4\right)\ne 0$,

$\left(x^2-3\right)\left(9x-4\right)\ne 0$,

$x^2-3\ne 0$, $9x-4\ne 0$

$x^2\ne 3$, $9x\ne 4$

$x\ne -\sqrt{3}$, $x\ne \sqrt{3}$, $x\ne \frac{4}{9}$.

Zatem $D=\mathrm{ℝ}\setminus \left\{-\sqrt{3};\frac{4}{9};\sqrt{3}\right\}$.

Zapiszmy licznik i mianownik ułamka algebraicznego $\frac{7x^3+2x^2-21x-6}{9x^3-4x^2-27x+12}$ w postaci iloczynowej stosując metodę grupowania wyrazów

$\frac{x^2\left(7x+2\right)-3\left(7x+2\right)}{\left(x+\sqrt{3}\right)\left(x-\sqrt{3}\right)\left(9x-4\right)}\ge 0$,

$\frac{\left(x^2-3\right)\left(7x+2\right)}{\left(x+\sqrt{3}\right)\left(x-\sqrt{3}\right)\left(9x-4\right)}\ge 0$,

$\frac{\left(x+\sqrt{3}\right)\left(x-\sqrt{3}\right)\left(7x+2\right)}{\left(x+\sqrt{3}\right)\left(x-\sqrt{3}\right)\left(9x-4\right)}\ge 0$.

Zauważmy, że mianownik mogliśmy zapisać od razu w postaci iloczynowej po obliczeniu dziedziny.

Po skróceniu ułamka otrzymujemy

$\frac{7x+2}{9x-4}\ge 0$.

Skorzystajmy z twierdzenia i zapiszmy nierówność wymierną jako równoważną nierówność wielomianową przy wyznaczonej dziedzinie nierówności wymiernej

$\frac{W_1\left(x\right)}{W_2\left(x\right)}\ge 0 \iff W_1\left(x\right)·W_2\left(x\right)\ge 0 \wedge W_2\left(x\right)\ne 0$,

$\frac{7x+2}{9x-4}\ge 0\iff \left(7x+2\right)\left(9x-4\right)\ge 0\wedge x\ne -\sqrt{3}$, $x\ne \sqrt{3}$, $x\ne \frac{4}{9}$.

Wielomian  $W\left(x\right)=63\left(x+\frac{2}{7}\right)\left(x-\frac{4}{9}\right)$ ma dwa pierwiastki: $\left(-\frac{2}{7}\right)$; $\frac{4}{9}$.

Uwzględniając dziedzinę nierówności wymiernej $D=\mathrm{ℝ}\setminus \left\{-\sqrt{3};\frac{4}{9};\sqrt{3}\right\}$ rysujemy szkic wykresu.

RUOt5wgTGv6dO

Ilustracja przedstawia poziomą oś X oraz wykres funkcji przyjmujący wartości dodanie w przedziale $(-\infty ;-\sqrt{3})\cup (-\sqrt{3};-\frac{2}{7}>\cup (\frac{4}{9};\sqrt{3})\cup (\sqrt{3};\infty )$ oraz wartości ujemne w przedziale $(-\frac{2}{7};\frac{4}{9})$.

Odpowiedź: Rozwiązaniem nierówności wymiernej jest zbiór $\left(-\infty ;-\sqrt{3}\right)\cup \left(-\sqrt{3};-\frac{2}{7}\right.⟩\cup \left(\frac{4}{9};\sqrt{3}\right)\cup \left(\sqrt{3};+\infty \right)$.

Wyznaczmy zbiór rozwiązań nieróności $\frac{8x^4+24x^3-x-3}{8x^5-32x^3-x^2+4}<\frac{-x-3}{x^2-4}$.

Rozwiązanie

Podajmy konieczne założenia: $8x^5-32x^3-x^2+4\ne 0$, $x^2-4\ne 0$

$8x^3\left(x^2-4\right)-\left(x^2-4\right)\ne 0$, $x^2\ne 4$

$\left(8x^3-1\right)\left(x^2-4\right)\ne 0$, $x\ne -2$, $x\ne 2$

$8x^3-1\ne 0$, $x^2-4\ne 0$, $x\ne -2$, $x\ne 2$

$8x^3\ne 1$, $x^2\ne 4$, $x\ne -2$, $x\ne 2$

$x\ne \frac{1}{2}$, $x\ne -2$, $x\ne 2$, $x\ne -2$, $x\ne 2$.

$D=\mathrm{ℝ}\setminus \left\{-2;\frac{1}{2};2\right\}$.

Zapiszmy licznik i mianownika ułamków algebraicznych w postaci iloczynowej stosując metodę grupowania wyrazów

$\frac{8x^3\left(x+3\right)-\left(x+3\right)}{8x^3\left(x^2-4\right)-\left(x^2-4\right)}<\frac{-x-3}{\left(x-2\right)\left(x+2\right)}$,

$\frac{\left(8x^3-1\right)\left(x+3\right)}{\left(8x^3-1\right)\left(x^2-4\right)}<\frac{-x-3}{\left(x-2\right)\left(x+2\right)}$.

Po skróceniu ułamka algebraicznego otrzymujemy nierówność

$\frac{x+3}{\left(x-2\right)\left(x+2\right)}<\frac{-x-3}{\left(x-2\right)\left(x+2\right)}$.

Zapiszmy nierówność w postaci ogólnej $\frac{W_1\left(x\right)}{W_2\left(x\right)}<0$

$\frac{x+3}{\left(x-2\right)\left(x+2\right)}-\frac{-x-3}{\left(x-2\right)\left(x+2\right)}<0$,

$\frac{x+3+x+3}{\left(x-2\right)\left(x+2\right)}<0$,

$\frac{2x+6}{\left(x-2\right)\left(x+2\right)}<0$.

Skorzystajmy z twierdzenia $\frac{W_1\left(x\right)}{W_2\left(x\right)}<0 \iff W_1\left(x\right)·W_2\left(x\right)<0 \wedge W_2\left(x\right)\ne 0$.

Zatem nierówność wymierną możemy zapisać w postaci równoważnej nierówności iloczynowej

$\frac{2x+6}{\left(x-2\right)\left(x+2\right)}<0\iff \left(2x+6\right)\left(x-2\right)\left(x+2\right)<0\wedge x\ne -2$, $x\ne \frac{1}{2}$, $x\ne 2$.

Wielomian $R\left(x\right)=2\left(x+3\right)\left(x-2\right)\left(x+2\right)$ ma trzy jednokrotne pierwiastki: $\left(-3\right)$, $\left(-2\right)$ oraz $2$.

Uwzględniając dziedzinę nierówności wymiernej $D=\mathrm{ℝ}\setminus \left\{-2;\frac{1}{2};2\right\}$ narysujemy szkic wykresu.

R1apc7aCZVNdK

Ilustracja przedstawia poziomą oś X oraz wykres funkcji przyjmujący wartości dodanie w przedziale $<-3;-2)\cup (2;\infty )$ oraz wartości ujemne w przedziale $(-\infty ;-3)\cup (-2;\frac{1}{2})\cup (\frac{1}{2};2)$.

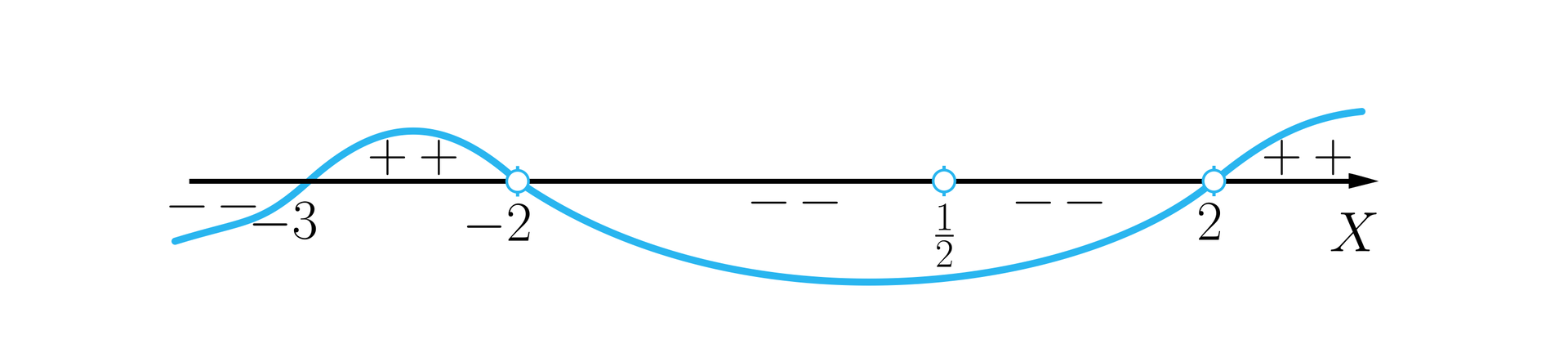
Odpowiedź: Zbiorem rozwiązań nierówności jest zbiór $\left(-\infty ;-3\right)\cup \left(-2;\frac{1}{2}\right)\cup \left(\frac{1}{2};2\right)$.

Obliczmy najmniejszą liczbę całkowitą $k$ spełniającą nierówność $\left|\frac{k^3-7k+6}{-3k^2+9k-6}+1\frac{1}{3}k\right|\le 2$.

Rozwiązanie

Podajmy konieczne założenie

$-3k^2+9k-6\ne 0$

$-3\left(k-1\right)\left(k-2\right)\ne 0$,

$k\ne 1$, $k\ne 2$.

$D=\mathrm{ℝ}\setminus \left\{1;2\right\}$.

Zapiszmy licznik  ułamka algebraicznego $\frac{k^3-7k+6}{-3k^2+9k-6}$ w postaci iloczynowej stosując metodę grupowania wyrazów

$\left|\frac{k^3-k-6k+6}{-3\left(k-1\right)\left(k-2\right)}+1\frac{1}{3}k\right|\le 2$,

$\left|\frac{k\left(k^2-1\right)-6\left(k-1\right)}{-3\left(k-1\right)\left(k-2\right)}+1\frac{1}{3}k\right|\le 2$,

$\left|\frac{k\left(k-1\right)\left(k+1\right)-6\left(k-1\right)}{-3\left(k-1\right)\left(k-2\right)}+1\frac{1}{3}k\right|\le 2$.

Wyłączmy przed nawias $k-1$ , stąd

$\left|\frac{\left(k-1\right)\left[k\left(k+1\right)-6\right]}{-3\left(k-1\right)\left(k-2\right)}+1\frac{1}{3}k\right|\le 2$,

$\left|\frac{\left(k-1\right)\left(k^2+k-6\right)}{-3\left(k-1\right)\left(k-2\right)}+1\frac{1}{3}k\right|\le 2$,

$\left|\frac{\left(k-1\right)\left(k-2\right)\left(k+3\right)}{-3\left(k-1\right)\left(k-2\right)}+1\frac{1}{3}k\right|\le 2$,

Po skróceniu ułamka algebraicznego otrzymujemy

$\left|\frac{k+3}{-3}+1\frac{1}{3}k\right|\le 2$,

$\left|-\frac{1}{3}k-1+1\frac{1}{3}k\right|\le 2$,

$\left|k-1\right|\le 2$.

R1D2lB15Kmx8i

Ilustracja przedstawia poziomą oś k od minus czterech do czterech oraz zaznaczony przedział nad osią $<-1;1)\cup (1;2)\cup (2;3>$.

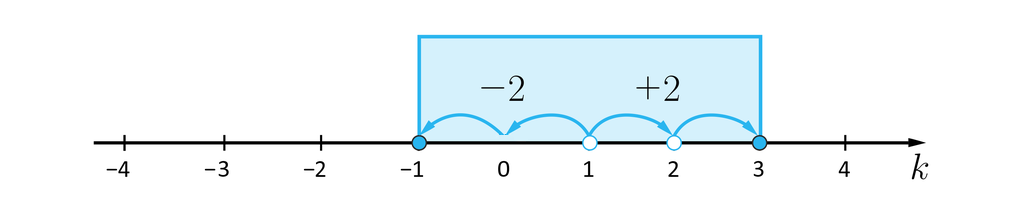
Odpowiedź: Najmniejszą liczbą całkowitą, która spełnia nierówność $\left|\frac{k^3-7k+6}{-3k^2+9k-6}+1\frac{1}{3}k\right|\le 2$ jest liczba $\left(-1\right)$.

dziedziną nierówności wymiernej są wszystkie liczby rzeczywiste za wyjątkiem pierwiastków wielomianu $W_2\left(x\right)$ znajdującego się w mianowniku danego wyrażenia $\frac{W_1\left(x\right)}{W_2\left(x\right)}$

$D=\mathrm{ℝ} \setminus \left\{x: W_2\left(x\right)=0\right\}$

pierwiastkiem wielomianu $W\left(x\right)$ nazywamy liczbę rzeczywistą $a$, dla której $W\left(a\right)=0$