Galeria zdjęć interaktywnych
Zapoznaj się z galerią zdjęć interaktywnych. Spróbuj najpierw samodzielnie rozwiązywać zamieszczone tam zdania, a dopiero następnie porównaj swoje rozwiązanie z przedstawionym w medium.
Wzorując się na przedstawionym w galerii zdjęć interaktywnych rozumowaniu, rozwiąż następujące zadanie:
Odcinek stanowi środkową trójkąta prostokątnego równoramiennego poprowadzoną z wierzchołka kąta prostego. Punkt dzieli bok na dwie równe części. Poprowadzono z niego odcinek łączący go z przeciwprostokątną, równoległy do . Pole otrzymanego w ten sposób trapezu prostokątnego wynosi .
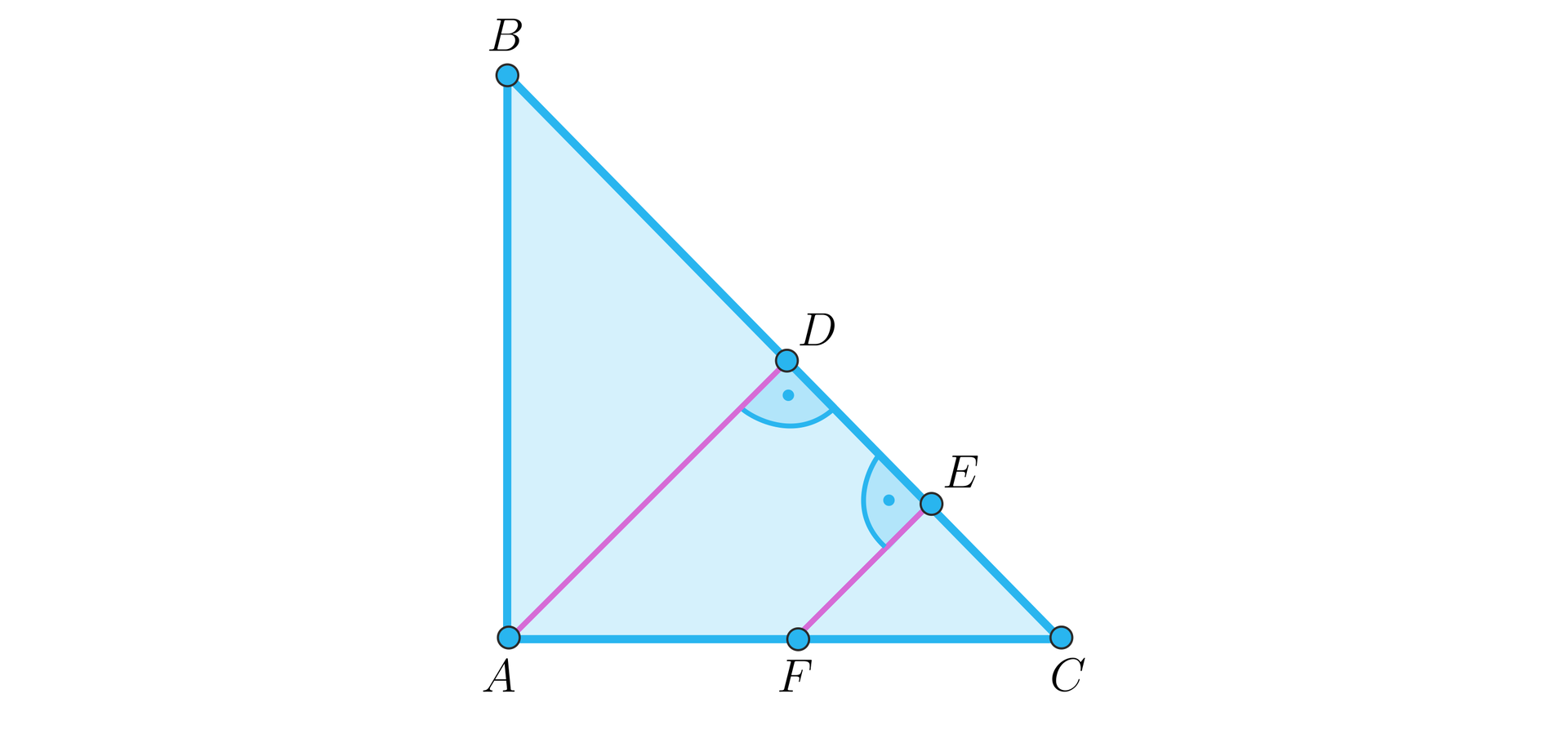
Oblicz pole trójkąta .
Spróbuj uzależnić pole trapezu od długości boku , a następnie obliczyć długość tego boku. Jest to możliwe do wykonania na kilka sposobów – każdy z nich jest równie dobry.
Oznaczmy długość ramienia trójkąta przez . Z punktu poprowadźmy wysokość trapezu – oznaczmy ją przez . Trójkąt jest prostokątny i równoramienny, co więcej, .
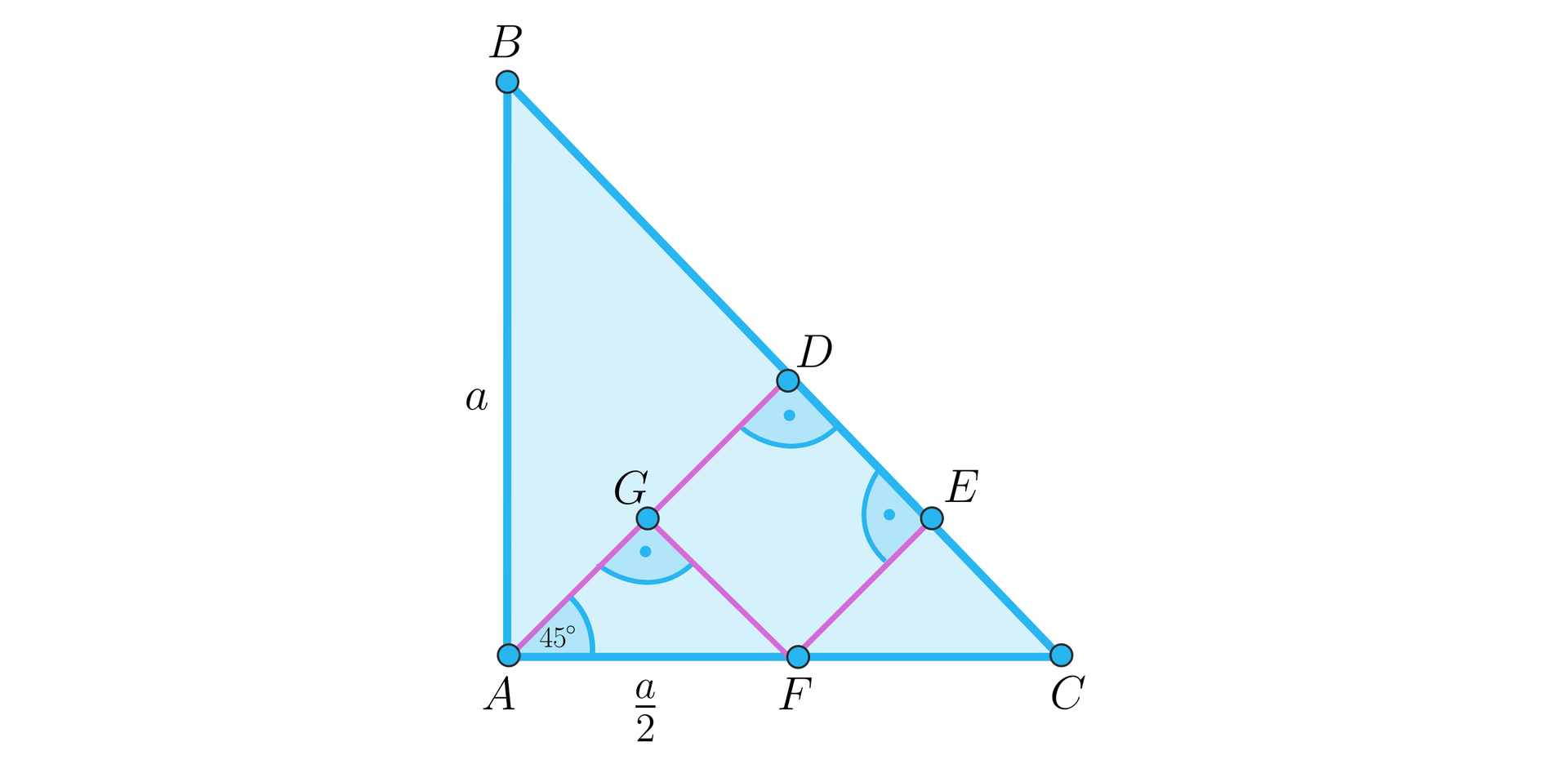
Korzystając z wartości sinusa , mamy:
Oczywiście .
Trójkąt także jest prostokątny i równoramienny, zatem podobnie możemy uzależnić od długość podstawy rozważanego trapezu.
Umożliwia nam to wyznaczenie długości odcinka – wynosi ona
Umożliwia nam to zauważenie, że czworokąt jest kwadratem.
Trapez możemy więc podzielić na kwadrat i trójkąt – których pola możemy opisać przy pomocy .
Uzyskujemy w ten sposób równanie kwadratowe, które łatwo jesteśmy w stanie rozwiązać:
Oczywiście odrzucamy wariant z ujemną wartoscią .
Możemy już łatwo obliczyć pole trójkąta , które wynosi
Odpowiedź:
.