Sprawdź się
Trójkąt o kątach , , nazywamy luka do uzupełnienia i prostokątnym.
Wartość luka do uzupełnienia wynosi .
Na podstawie załączonego rysunku zaznacz poprawną odpowiedź.
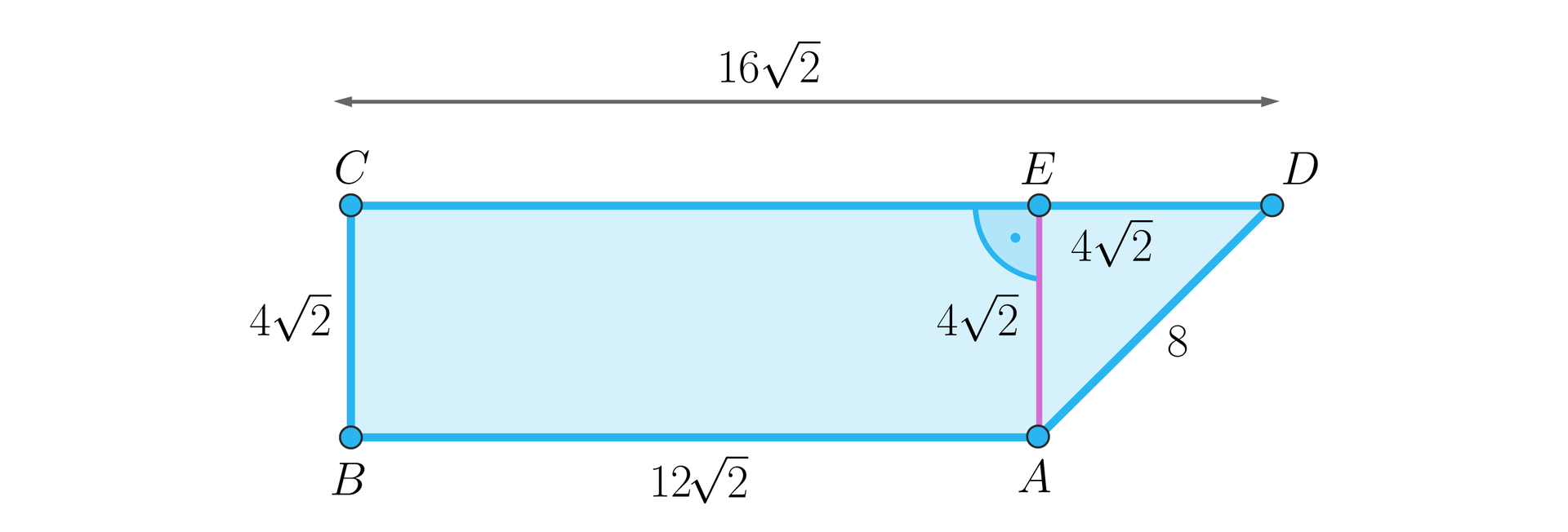
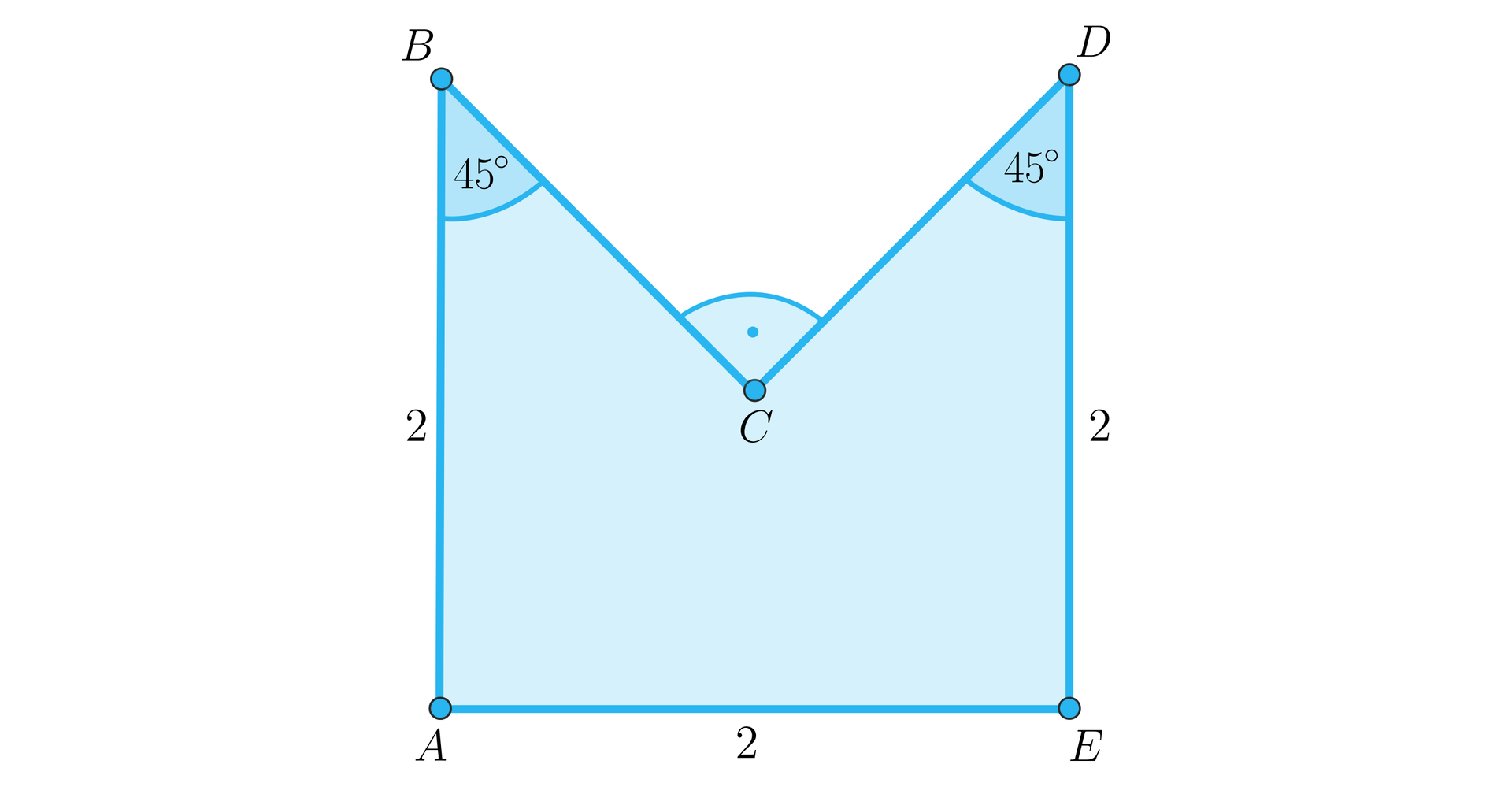
Na podstawie załączonego rysunku oblicz ile wynosi pole poniższego trapezu.

Punkt jest punktem przecięcia się przekątnych kwadratu .
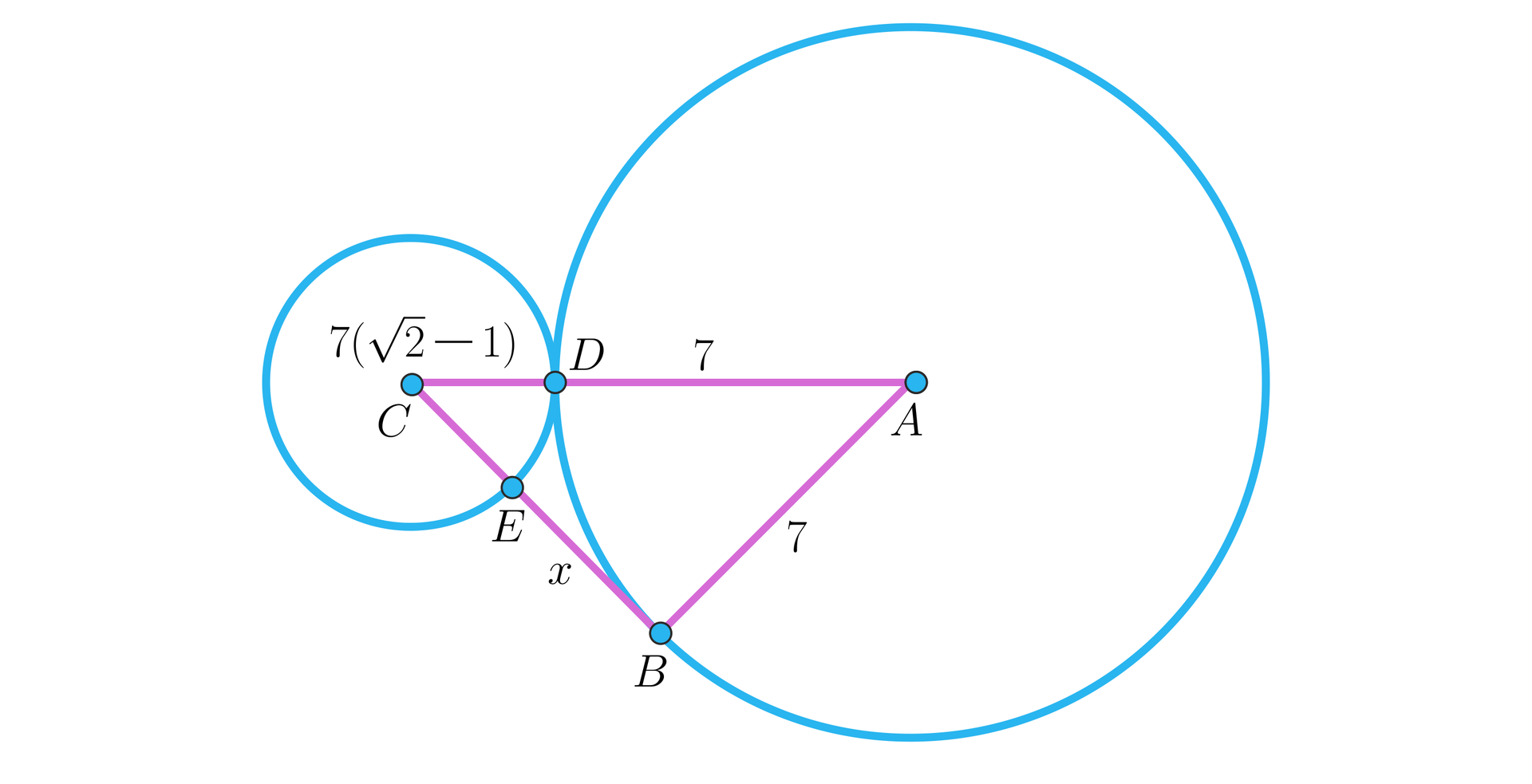
Do zadanego okręgu o środku w punkcie i promieniu dorysowany został styczny okrąg o promieniu i środku w punkcie . Z punktu poprowadzono styczną do pierwszego okręgu, a punkt styczności oznaczono literą . Oznaczmy punkt przecięcia tej stycznej i mniejszego okręgu przez . Oblicz długość odcinka .
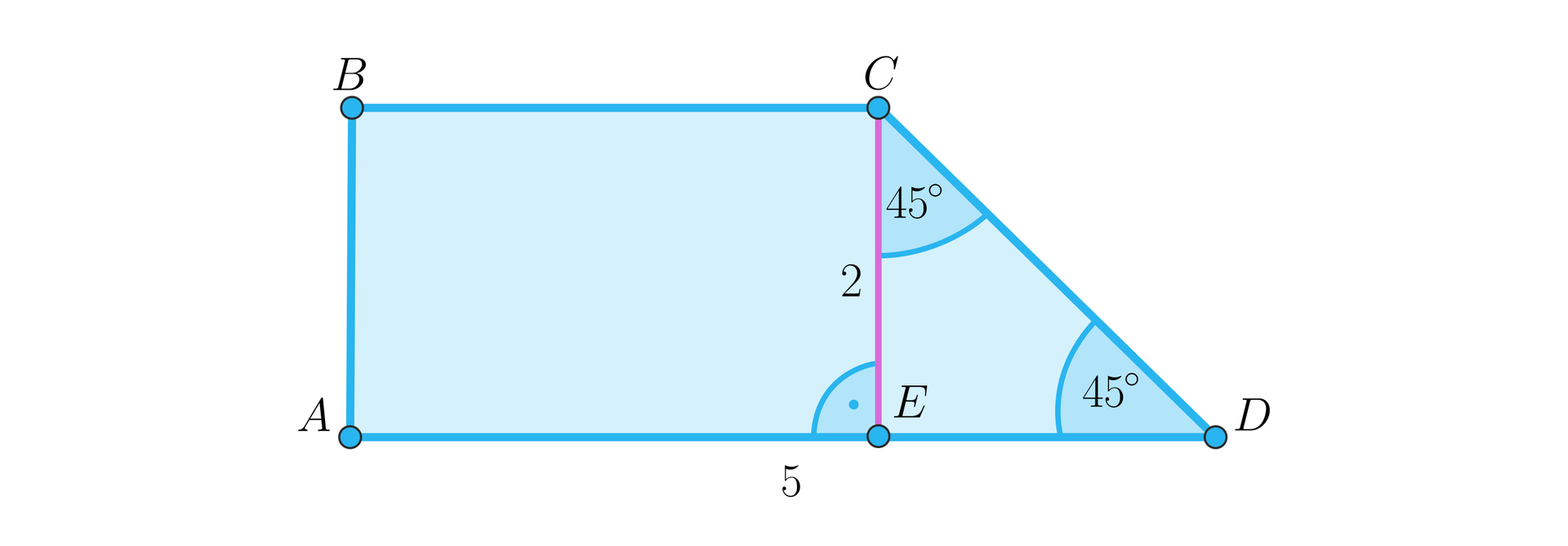
Dany jest trapez, w którym podstawy mają długości i , zaś bok , będący dłuższym z jego ramion tworzy z podstawą kąt o mierze . Oblicz obwód tego trapezu, jeżeli jego pole wynosi .
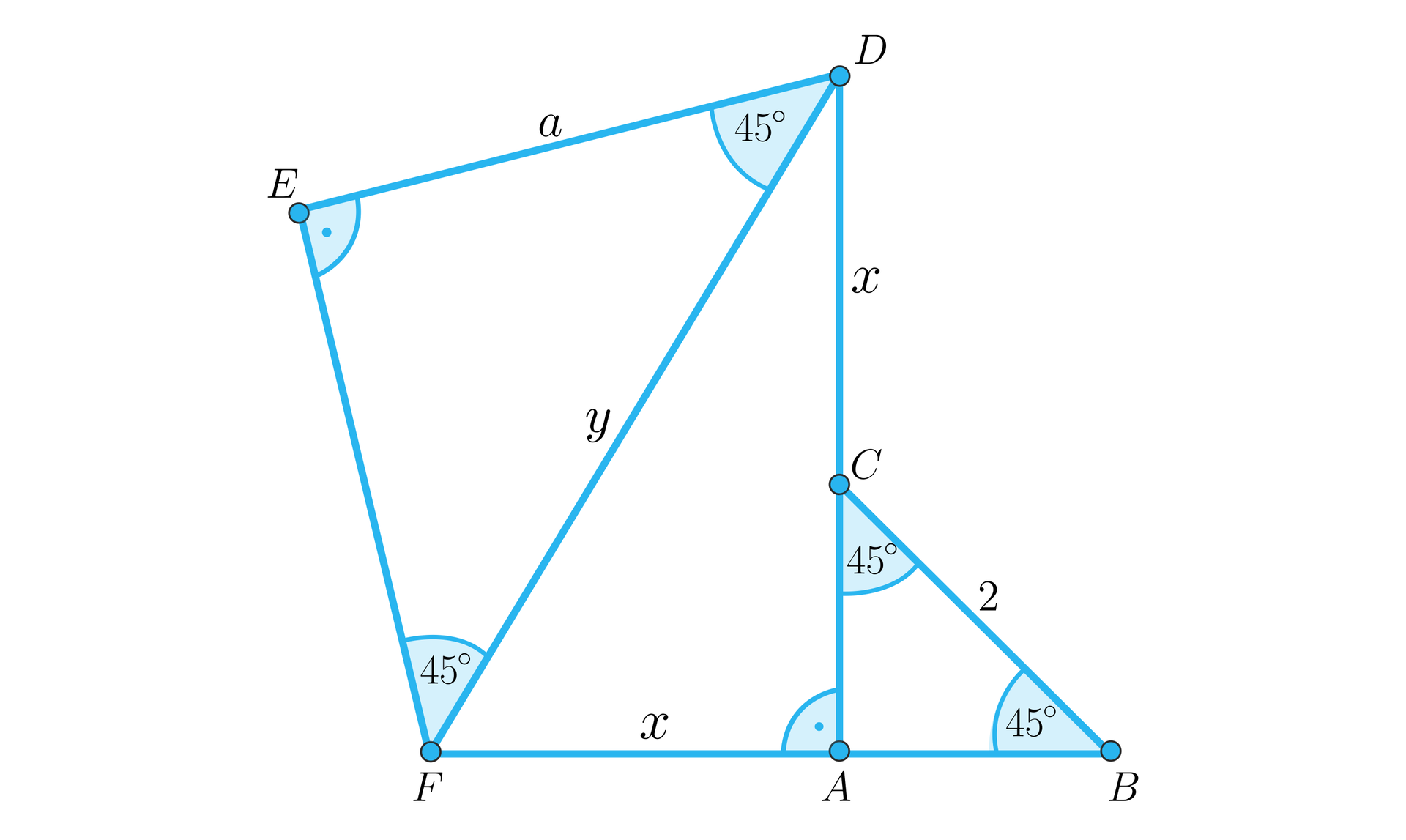
Korzystając z danych przedstawionych na poniższym rysunku, wyznacz długość boku , jeżeli .