Galeria zdjęć interaktywnych
Polecenie 1
Zapoznaj się z galerią zdjęć interaktywnych, a następnie rozwiąż kolejne polecenia.
Ilustracja pierwsza. Ustal współrzędne punktu, w którym przecinają się wykresy funkcji i .
rozwiązanie. Rysujemy wykresy funkcji f oraz g w jednym układzie współrzędnych i odczytujemy, że przecinają się one w punkcie P o współrzędnych . Aby upewnić się, że tak jest obliczamy. i . Odpowiedź. Wykresy funkcji i przecinają się w punkcie .
Ilustracja pierwsza. Ustal współrzędne punktu, w którym przecinają się wykresy funkcji i .
rozwiązanie. Rysujemy wykresy funkcji f oraz g w jednym układzie współrzędnych i odczytujemy, że przecinają się one w punkcie P o współrzędnych . Aby upewnić się, że tak jest obliczamy. i . Odpowiedź. Wykresy funkcji i przecinają się w punkcie .
rozwiązanie. Rysujemy wykresy funkcji f oraz g w jednym układzie współrzędnych i odczytujemy, że przecinają się one w punkcie P o współrzędnych . Aby upewnić się, że tak jest obliczamy. i . Odpowiedź. Wykresy funkcji i przecinają się w punkcie .
Ilustracja druga.
Wykaż, że układ równań nie ma rozwiązań.
Rozwiązanie.
Jeśli pomnożymy stronami pierwsze równanie przez 3 to otrzymamy układ . Odpowiedź.
Lewe strony równań są sobie równe, a prawe - różne. Jest zatem układ sprzeczny.
Ilustracja druga.
Wykaż, że układ równań nie ma rozwiązań.
Rozwiązanie.
Jeśli pomnożymy stronami pierwsze równanie przez 3 to otrzymamy układ . Odpowiedź.
Lewe strony równań są sobie równe, a prawe - różne. Jest zatem układ sprzeczny.Ilustracja trzecia. Prosta k przechodzi przez punkty A o współrzędnych oraz B o współrzędnych . Jakie jest jej równanie.
a kierunkowe
b ogólne.
rozwiązanie.
a równanie kierunkowe prostej jest postaci , musimy znaleźć liczby a oraz b należy do prostej , zatem zachodzi równość:, należy do prostej , zatem zachodzi równość:
Ilustracja trzecia. Prosta k przechodzi przez punkty A o współrzędnych oraz B o współrzędnych . Jakie jest jej równanie. a kierunkowe
b ogólne.
rozwiązanie.
a równanie kierunkowe prostej jest postaci , musimy znaleźć liczby a oraz b należy do prostej , zatem zachodzi równość:, należy do prostej , zatem zachodzi równość:
a kierunkowe
b ogólne.
rozwiązanie.
a równanie kierunkowe prostej jest postaci , musimy znaleźć liczby a oraz b należy do prostej , zatem zachodzi równość:, należy do prostej , zatem zachodzi równość:
Ilustracja piąta.
Rozwiązanie. A. rozwiązanie kierunkowe prostej jest postaci , musimy znaleźć liczby a oraz b . Punkt A należy do prostej k zatem zachodzi równość punkt b również należy do prostej k więc . Rozwiązując układ równań . Uzyskujemy a równe trzy oraz b równe minus pięć.
Równanie kierunkowe prostej.
Ilustracja piąta.
Rozwiązanie. A. rozwiązanie kierunkowe prostej jest postaci , musimy znaleźć liczby a oraz b . Punkt A należy do prostej k zatem zachodzi równość punkt b również należy do prostej k więc . Rozwiązując układ równań . Uzyskujemy a równe trzy oraz b równe minus pięć.
Równanie kierunkowe prostej.Ilustracja szósta. B. zamienimy równanie kierunkowe na ogólne. ,.
Równanie kierunkowe prostej.
Ilustracja szósta. B. zamienimy równanie kierunkowe na ogólne. ,.
Równanie kierunkowe prostej.Ilustracja siódma. Ania mówi do kasi. Gdy będziesz w moim wieku to ja będę miała 24 lata. Gdy ja byłam w twoim wieku to ty byłaś ode mnie dwa razy młodsza. Ile lat ma obecnie kasia, a ile ania?
Rozwiązanie.
Wprowadźmy oznaczenia. X to obecny wiek ani. Y to obecny wiek kasi.
Różnica wieku będzie równa x minus y więc kasia będzie w wieku ani za x minus y lat. Wtedy ania będzie mieć . Ania miała y lat x minus y lat temu. Wtedy kasia miała lat i była dwa razy młodsza od ani więc. . Uzyskamy układ równań. . Korzystamy z metody przeciwnych współczynników. Dodając oba równania stronami otrzymujemy. 2y równe 24 i y równe dwanaście.
Podstawiając te wartość do pierwszego równania mamy czyli x równe osiemnaście. Odpowiedź. Ania ma teraz lat, a Kasia .
Ilustracja siódma. Ania mówi do kasi. Gdy będziesz w moim wieku to ja będę miała 24 lata. Gdy ja byłam w twoim wieku to ty byłaś ode mnie dwa razy młodsza. Ile lat ma obecnie kasia, a ile ania?
Rozwiązanie.
Wprowadźmy oznaczenia. X to obecny wiek ani. Y to obecny wiek kasi.
Różnica wieku będzie równa x minus y więc kasia będzie w wieku ani za x minus y lat. Wtedy ania będzie mieć . Ania miała y lat x minus y lat temu. Wtedy kasia miała lat i była dwa razy młodsza od ani więc. . Uzyskamy układ równań. . Korzystamy z metody przeciwnych współczynników. Dodając oba równania stronami otrzymujemy. 2y równe 24 i y równe dwanaście.
Podstawiając te wartość do pierwszego równania mamy czyli x równe osiemnaście. Odpowiedź. Ania ma teraz lat, a Kasia .Polecenie 2
W którym punkcie przecinają się proste o równaniach:
oraz ?
Rozwiązujemy układ równań:. Stąd i mamy oraz . Proste przecinają się w punkcie .
Polecenie 3
Rozwiąż metodą graficzną układ równań:
Wyznacz równania prostych w postaci kierunkowej odpowiadające każdemu z równań. Opisz ich wykresy w układzie współrzędnych.
.
Rysujemy w układzie współrzędnych proste: oraz .
Szukane proste mają równania postaci: oraz . Zauważmy, że dwie proste nie są do siebie równoległe, a więc będą się przecinać w jednym punkcie. Aby go wyznaczyć można rozwiązać układ równań metodą przeciwnych współczynników lub metodą podstawiania. Zatem oraz .
Ilustracja przedstawia układ współrzędnych z pionową osią od minus 3 do czterech oraz osią poziomą od minus 3 do czterech. Zaznaczono dwie proste malejące. przecinające się w punkcie P w czwartej ćwiartce układu.
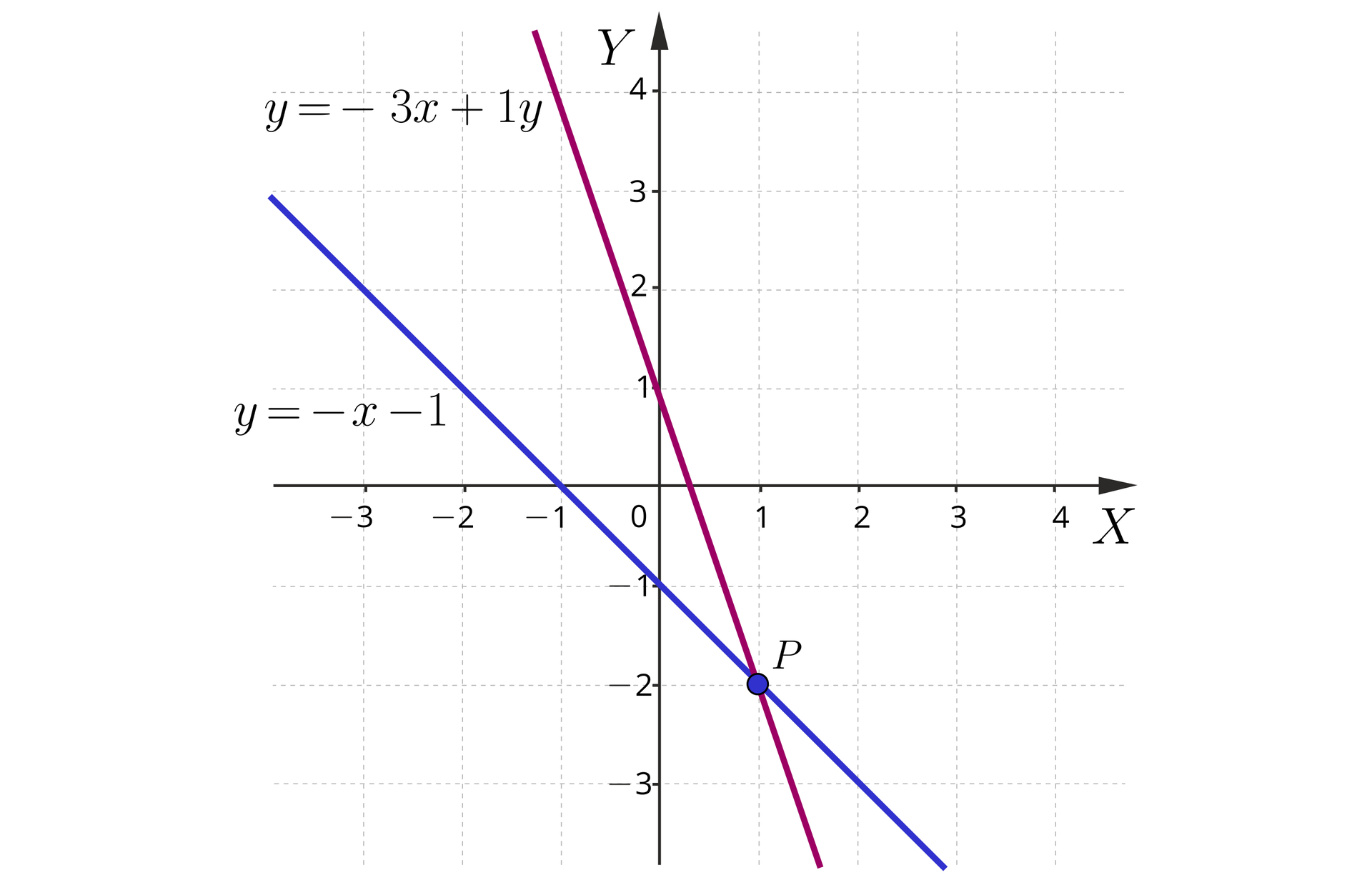
Proste przecinają się w punkcie .
Polecenie 4
Trzeba zapakować towaru do skrzynek dwóch rodzajów: mniejszych, mieszczących , i większych na . Ile trzeba wziąć skrzynek mniejszych, a ile większych?
Rozwiązujemy układ równań: . Trzeba wziąć mniejszych skrzynek i większych.