Przeczytaj
Równanie linii prostej, która jest wykresem funkcji liniowej, zapisywaliśmy dotąd w postaci:
Postać taką nazywamy postacią kierunkową, bowiem od razu widzimy, jaki jest współczynnik kierunkowy rozważanej prostejprostej.
W postaci kierunkowej nie można jednak zapisać równań prostych równoległych do osi , gdyż ich współczynnik kierunkowy nie jest określony. Dlatego, aby móc rozważać jednocześnie wszystkie rodzaje prostych na płaszczyźnie, używamy często zapisu równania prostej w postaci ogólnej:
gdzie , oraz są ustalonymi liczbami rzeczywistymi.
Oczywiście, jeśli dana prostaprosta jest wykresem funkcji liniowej, to jej równanie zawsze można zapisać w obu postaciach.
Równanie prostej zapisane w postaci ogólnej:
możemy zapisać w postaci kierunkowej:
.
Równanie prostej zapisane w postaci kierunkowej:
możemy zapisać w postaci ogólnej:
.
Zapis równania prostej w postaci ogólnej lub kierunkowej często pojawia się w układach równań liniowych. Sposoby rozwiązywania takich układów to np. metoda podstawiania lub przeciwnych współczynników. Pokażemy, że rozwiązywanie układu równań liniowych można zinterpretować jako poszukiwanie punktu przecięcia pewnych prostych w układzie współrzędnych.
Rozwiążemy metodą podstawiania układ równań: .
Z drugiego równania wyznaczamy w zależności od , a następnie otrzymane wyrażenie podstawiamy do pierwszego równania:
Rozwiązaniem układu równań jest więc para liczb oraz .
Zobaczymy teraz, że ten sam wynik możemy uzyskać, rysując pewne proste w układzie współrzędnych.
Rozwiążemy ten sam układ równań metodą graficzną. W tym celu przekształcamy oba równania do postaci kierunkowej:
.
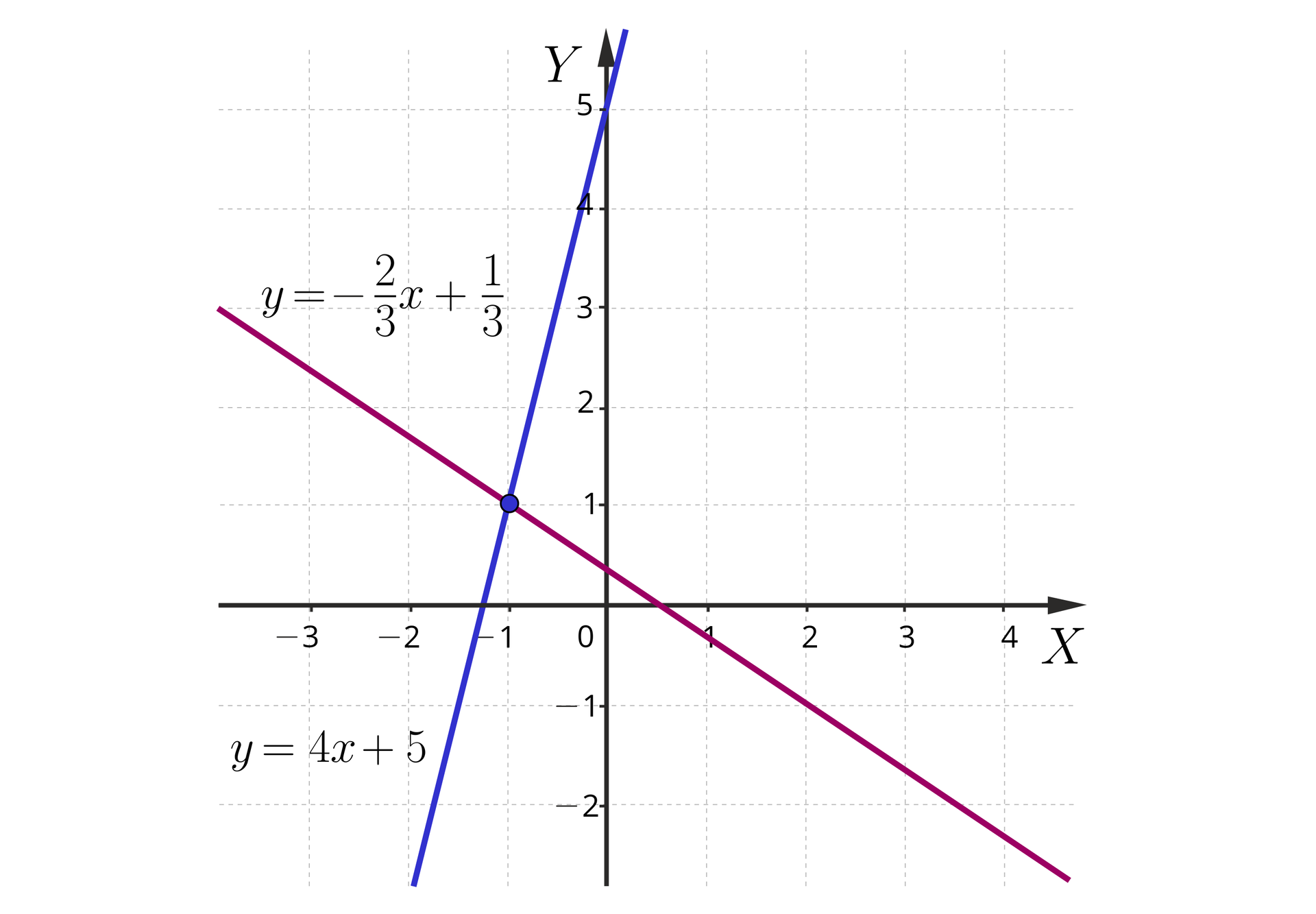
Aby odczytać rozwiązanie powyższego układu, poszukujemy punktu, który należy jednocześnie do prostej oraz do prostej . Z rysunku odczytujemy, że obie proste przecinają się w punkcie . Zatem metodą graficzną otrzymujemy to samo, co metodą algebraiczną, rozwiązanie układu równań : oraz .
Interpretacja geometryczna układu równań liniowych pozwala lepiej zrozumieć, dlaczego układ taki może mieć albo dokładnie jedno rozwiązanie, albo nieskończenie wiele, albo zero rozwiązań. Rozpatrzmy układ równań postaci:
Para liczb oraz jest rozwiązaniem tego układu wtedy i tylko wtedy, gdy punkt o współrzędnych należy jednocześnie do prostej i do prostej .
Rozwiązanie układu równań polega na znalezieniu punktów wspólnych dwóch prostych na płaszczyźnie, zatem układ dwóch równań liniowych:
nie ma rozwiązań, gdy proste są równoległe i się nie pokrywają,
ma nieskończenie wiele rozwiązań, gdy proste się pokrywają,
ma dokładnie jedno rozwiązanie, gdy proste się przecinają.
Układ równań:
nie ma rozwiązań, ponieważ proste o równaniach oraz są równoległe i nie mają punktów wspólnych.

Układ równań:
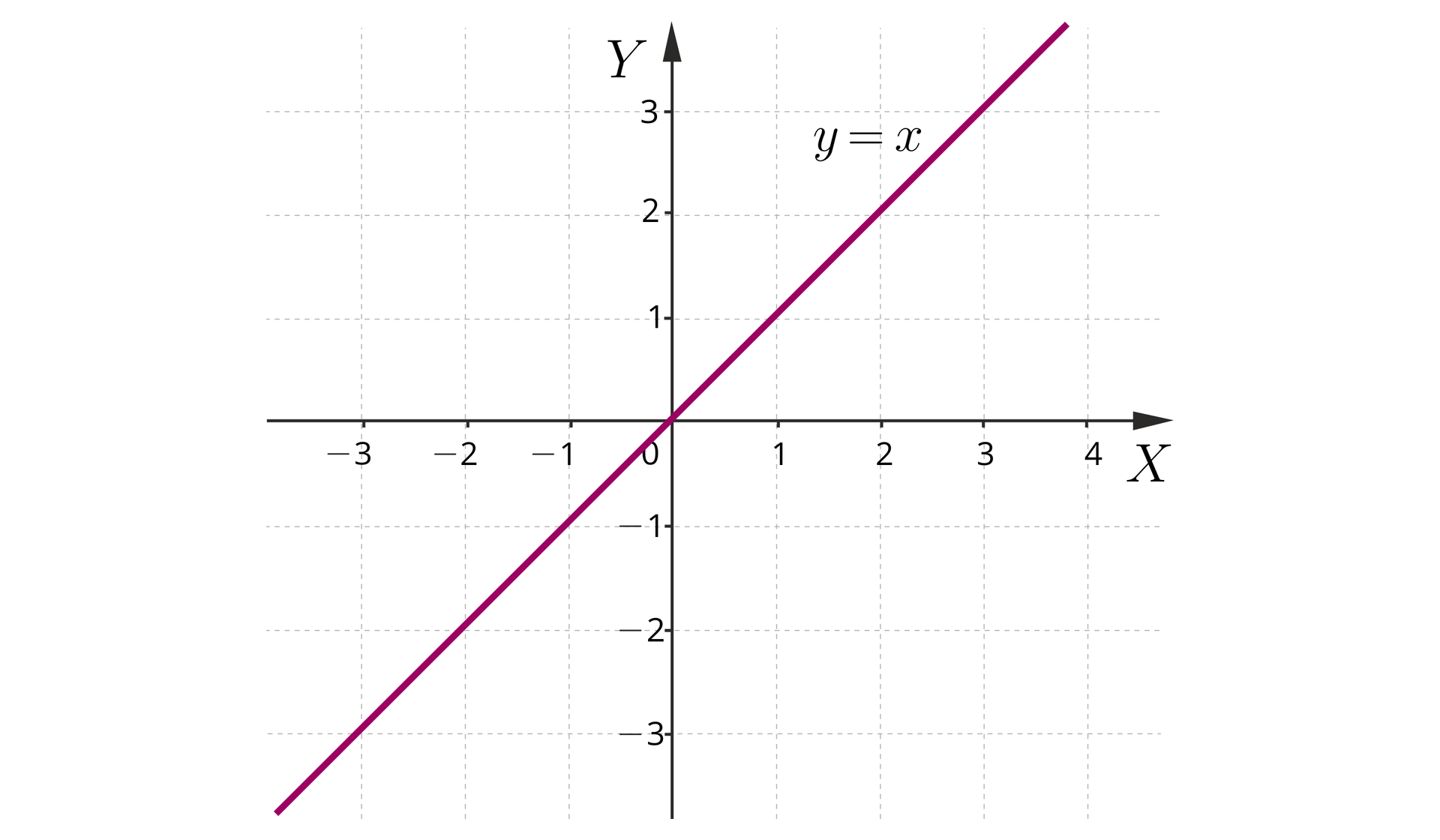
ma nieskończenie wiele rozwiązań, gdyż wyznaczając z obu równań , uzyskamy równanie tej samej prostej: .
Układ równań:
ma dokładnie jedno rozwiązanie, ponieważ proste oraz przecinają się w punkcie . A zatem jedynym rozwiązaniem układu jest para liczb , .
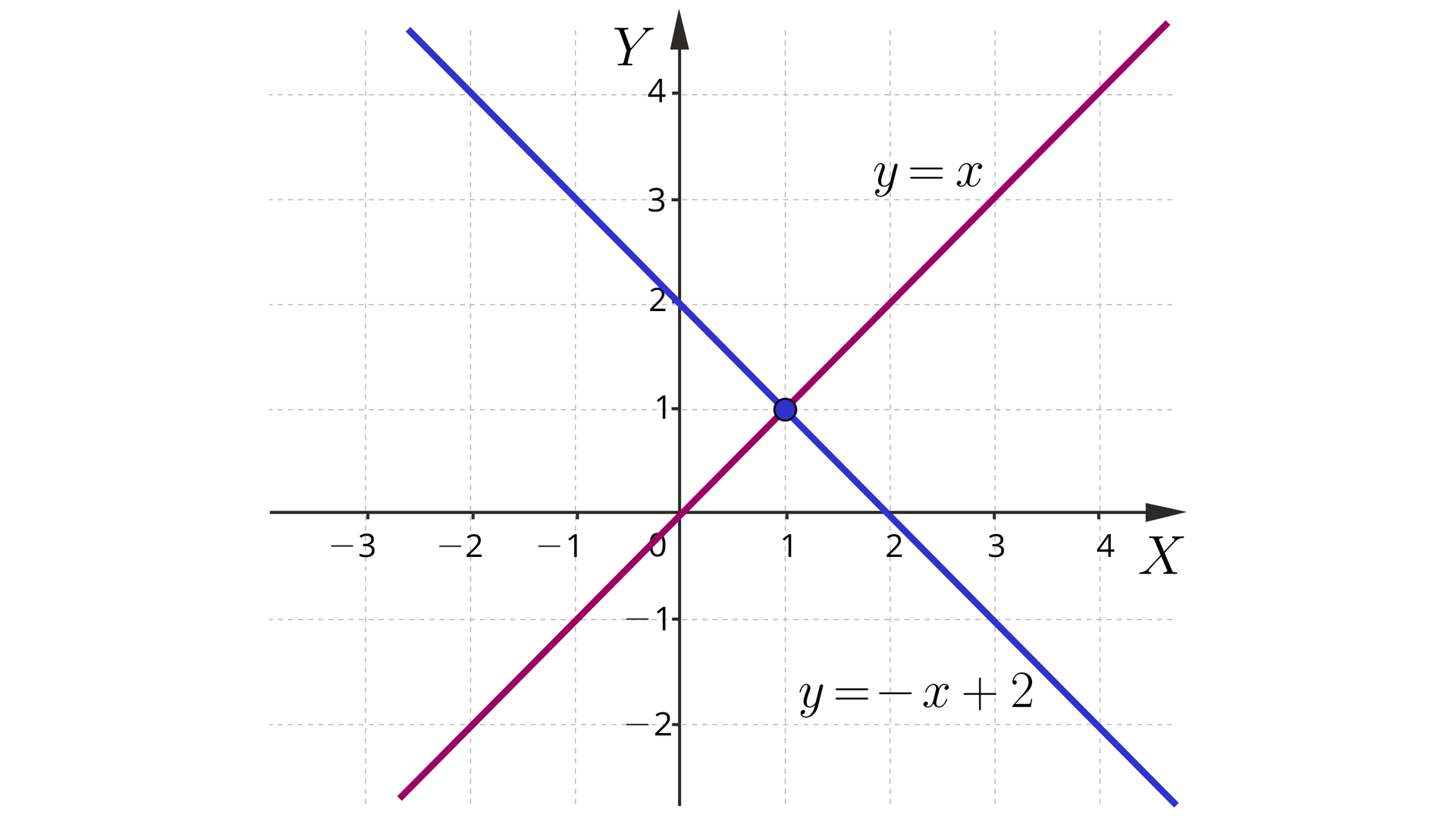
Należy jeszcze sprawdzić, czy na pewno dobrze odczytaliśmy współrzędne z rysunku:
Słownik
zbiór punktów opisanych następującym równaniem ogólnym , gdzie i nie mogą być równocześnie równe zeru, a jest dowolną liczbą rzeczywistą