Galeria zdjęć interaktywnych
Zapoznając się z galerią zdjęć interaktywnych, spróbuj najpierw samodzielnie rozwiązywać zamieszczone tam zadania, a dopiero następnie porównaj rozwiązania.
Na rysunku połączono punkty tworząc odcinki GF oraz HE
Na rysunku połączono punkty tworząc odcinki GF oraz HE
Na ilustracji czworokąta połączono środki boków tworząc równoległobok. Warto zauważyć, że teza jest prawdziwa również dla czworokąta wklęsłego.
Ilustracja przedstawia czworokąt wklęsły ABCD. Odcinek GH znajduję się w środku czworokąta, a odcinek FE poza obszarem czworokąta.
Na ilustracji czworokąta połączono środki boków tworząc równoległobok. Warto zauważyć, że teza jest prawdziwa również dla czworokąta wklęsłego.
Ilustracja przedstawia czworokąt wklęsły ABCD. Odcinek GH znajduję się w środku czworokąta, a odcinek FE poza obszarem czworokąta.
Na ilustracji czworokąta połączono odcinki AD, NE oraz GM. Na podstawie twierdzenia odwrotnego do twierdzenia Talesa wnioskujemy, równoległość odcinków i do boku .
Na ilustracji czworokąta połączono odcinki BC, EM oraz NG
Na ilustracji czworokąta połączono odcinki AD, NE oraz GM. Na podstawie twierdzenia odwrotnego do twierdzenia Talesa wnioskujemy, równoległość odcinków i do boku .
Na ilustracji czworokąta połączono odcinki BC, EM oraz NG
Na ilustracji czworokąta zaznaczono odcinki AD i CB oraz utworzono równoległobok EMGN
Na ilustracji czworokąta zaznaczono odcinki AD i CB oraz utworzono równoległobok EMGN
Aby otrzymać tezę, wystarczy zauważyć, że pomarańczowe odcinki to przekątne tych równoległoboków i skorzystać z faktu, że przekątne równoległoboku się połowią.
Podsumowując:
przekątna równoległoboku przecina przekątną w połowie oraz przekątna równoległoboku przecina przekątną w połowie, więc wnioskujemy, że trzy pomarańczowe odcinki przecinają się w jednym punkcie, który jest środkiem tych odcinków.
Aby otrzymać tezę, wystarczy zauważyć, że pomarańczowe odcinki to przekątne tych równoległoboków i skorzystać z faktu, że przekątne równoległoboku się połowią.
Podsumowując:
przekątna równoległoboku przecina przekątną w połowie oraz przekątna równoległoboku przecina przekątną w połowie, więc wnioskujemy, że trzy pomarańczowe odcinki przecinają się w jednym punkcie, który jest środkiem tych odcinków.
Przekątne czworokąta przecinają się pod kątem prostym. Ich długości to odpowiednio i . Oblicz pole czworokąta, którego wierzchołkami są środki boków czworokąta .
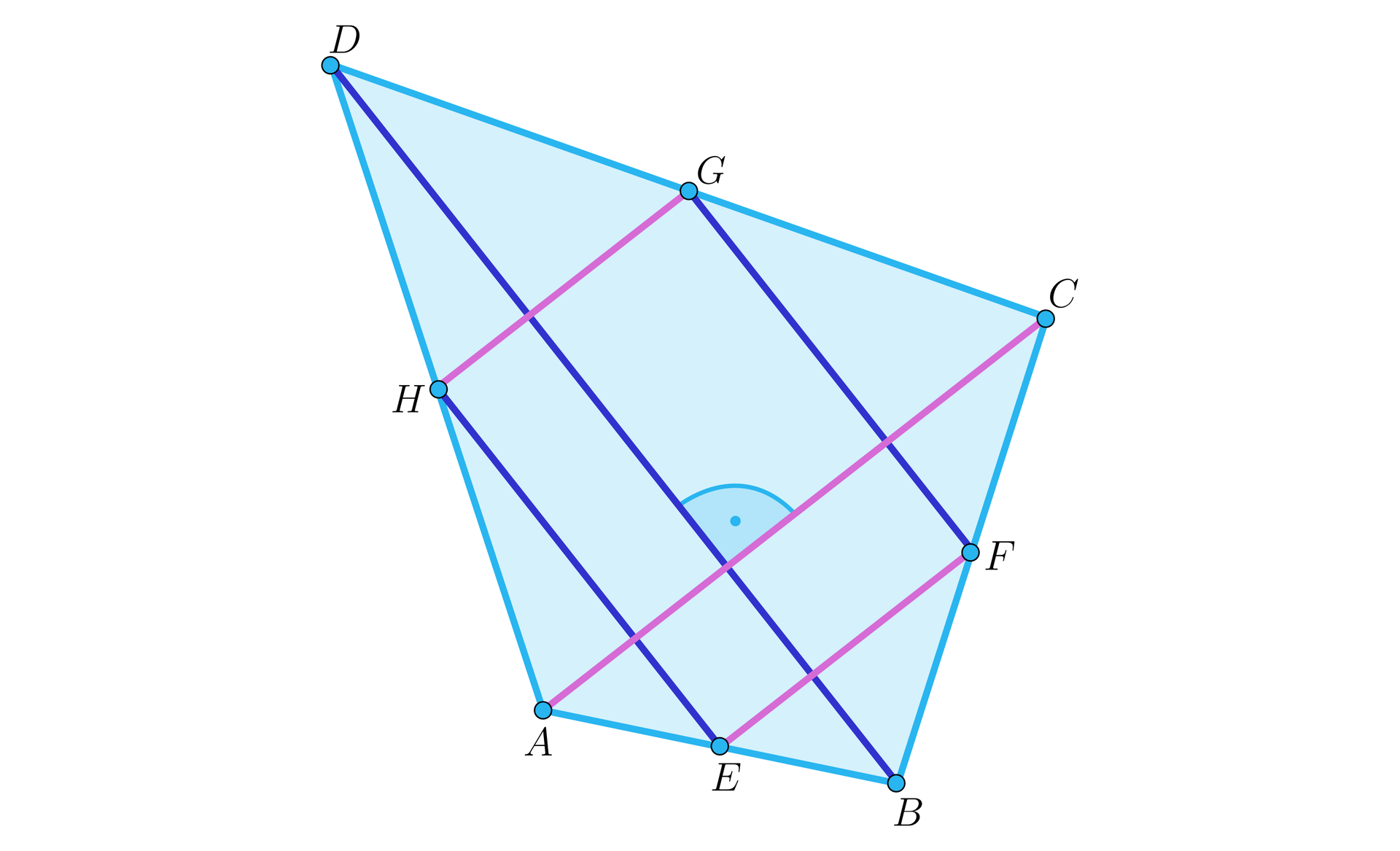
Oznaczmy środki boków , , , odpowiednio , , , . Korzystając z twierdzenia o odcinku łączącego środki boków w trójkącie lub z twierdzenia odwrotnego do twierdzenia Talesa otrzymujemy, że proste oraz są równoległe do przekątnej . Podobnie proste i są równoległe do przekątnej . Z założeń zadania wiemy, że przekątne są prostopadłe, zatem odpowiednie pary prostych równoległych do tych przekątnych również są prostopadłe. Wnioskujemy stąd, że czworokąt jest prostokątem. Ponownie wykorzystując twierdzenie o odcinku łączącym środki ramion w trójkącie otrzymujemy, że długości boków tego czworokąta mają długość równą połowie równoległej do nich przekątnej. Zatem pole czworokąta jest równe .