Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Na bokach $B C$ i $C D$ wybrano taki punkty $M$ i $N$ , że $\frac{|B M|}{|M C|} = \frac{|A N|}{|N D|}$ .

R1Dnq0koRJbq3

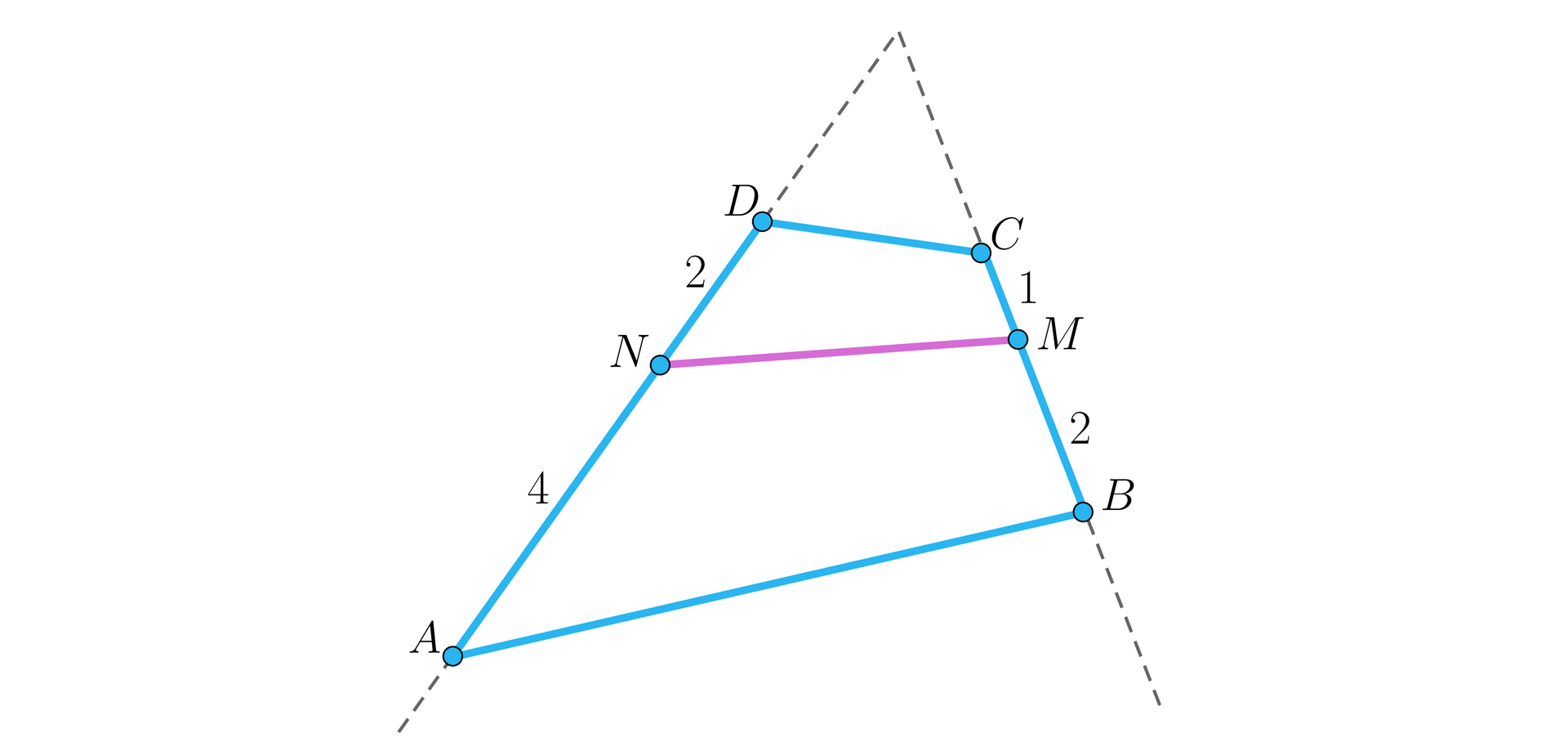
Ilustracja przedstawia czworokąt ABCD. Na boku AD umieszczono punkt N oddzielający bok na dwa odcinki, AN o długości 4 oraz ND o długości dwa. Na boku BC umieszczono punkt M oddzielający bok na dwa odcinki, CM o długości 1 oraz MB o długości dwa. Zaznaczono odcinek MN

R1bTyzf8ieYrE

Zaznacz prawidłową odpowiedź.

Prosta $M N$ jest równoległa do $A B$ .
Prosta $M N$ jest równoległa do $C D$ .
Prosta $A B$ jest równoległa do $C D$ .
Gdyby proste $A B$ i $C D$ były równoległe, to prosta $M N$ byłaby równoległa do $A B$ i do $C D$ .

R1Mr8L4ZcSMYw1

Ćwiczenie 2

W czworokącie $A B C D$ punkt $K$ jest środkiem boku $A D$ ,
$M$ - środkiem przekątnej $A C$ , $N$ - środkiem przekątnej $B D$ ,
$L$ - środkiem boku $B C$ . Wskaż zadania prawdziwe.

Proste $K M$ i $N L$ są równoległe.
Proste $M N$ i $K L$ są równoległe.
Odcinek $K N$ jest równoległy do odcinka $A B$ .
Punkty $K$ , $M$ , $N$ leżą na jednej prostej.
Gdy $A B | | C D$ to punkty $K$ , $M$ , $N$ , $L$ leżą na jednej prostej.

Ćwiczenie 3

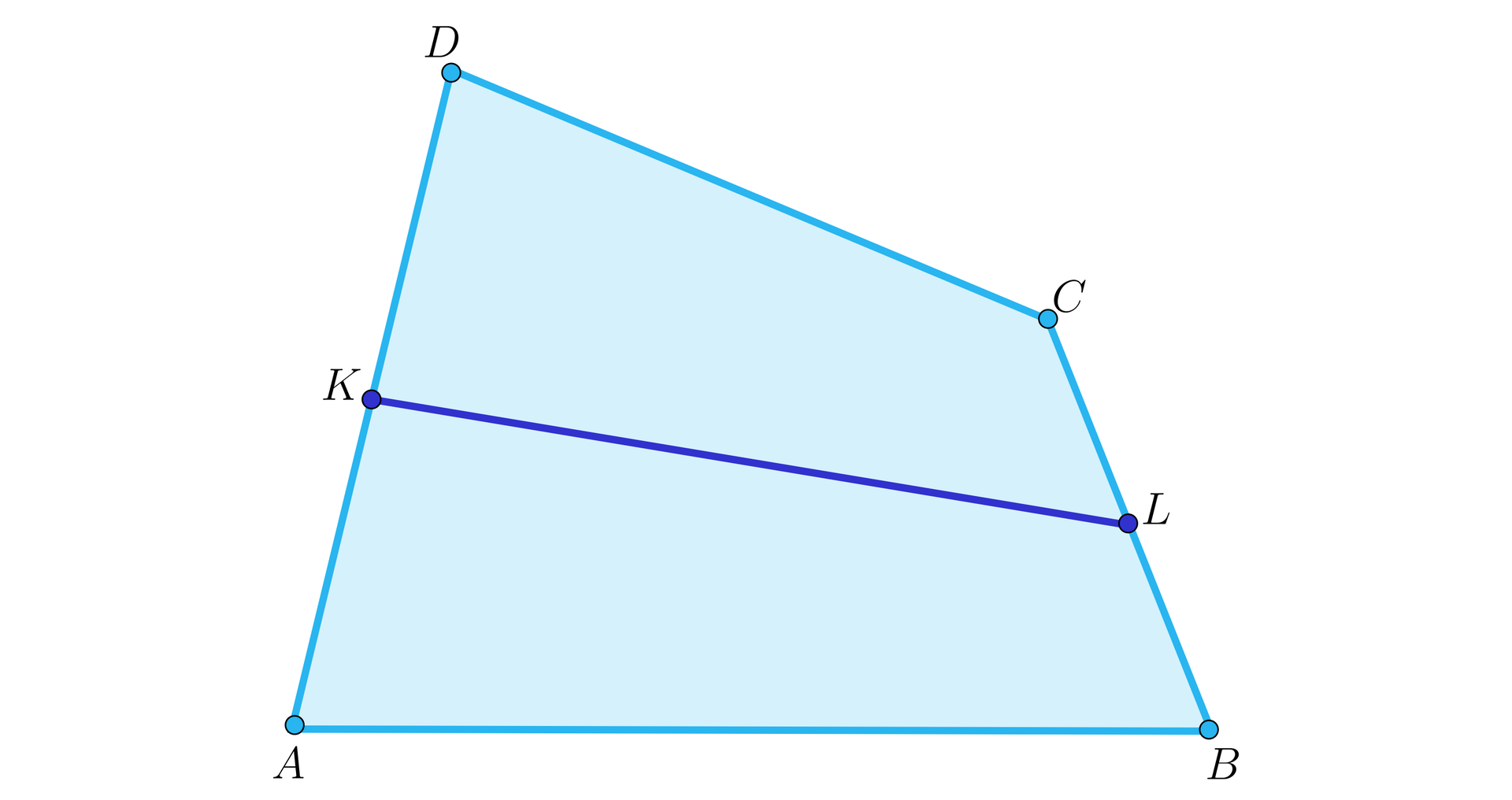
Dany jest czworokąt wypukły $A B C D$ . Punkty $K$ i $L$ są odpowiednio środkami boków $A D$ i $B C$ (rysunek). Udowodnij, że $|K L| \leq \frac{1}{2} (|A B| + |C D|)$ .

Rm4vyhDaSGmht

Ilustracja przedstawia czworokąt wypukły ABCD. Punkty K i L są środkami boków AD i BC. Zaznaczono odcinek KL.

RT65XUg4S3SD5

Ilustracja przedstawia czworokąt wypukły ABCD. Punkty K i L są środkami boków AD i BC. Zaznaczono odcinek KL. Zaznaczono przekątną AC i połączono ją z bokiem CD. Na środku przekątnej umieszczono punkt M, który połączono z punktami K oraz L.

Oznaczmy przez $M$ środek przekątnej $A C$ . Na podstawie twierdzenia odwrotnego do twierdzenia Talesa wnioskujemy, że proste $K M$ i $D C$ są równoległe oraz $|K M| = \frac{1}{2} |C D|$ . Analogicznie udowadniamy, że proste $M L$ i $A B$ są równoległe oraz $|M L| = \frac{1}{2} |A B|$ . Wykorzystując nierówność trójkąta otrzymujemy $|K L| \leq |K M| + |M L| = \frac{1}{2} |C D| + \frac{1}{2} |A B|$ . Warto zauważyć, że równość zachodzi wtedy i tylko wtedy, gdy punkt $M$ leży na odcinku $K L$ , a to ma miejsce wtedy i tylko wtedy, gdy proste $A B$ i $C D$ są równoległe.

R1C1uOIHRbq7i2

Ćwiczenie 4

Przekątne

A C

B D

czworokąta

A B C D

przecinają się w punkcie

P

. Na odcinku

A P

zaznaczono punkt

E

, natomiast na odcinku

B D

punkt

F

. Znając długości odcinków:

|A E| = 3

|E P| = 2

|P C| = 1

oraz

|B F| = 6

|F P| = 4

|P D| = 2

dopasuj proporcję odcinków powstałych na przekątnych do równoległości odpowiednich prostych.

\frac{1}{5} = \frac{2}{10}

Możliwe odpowiedzi: 1.

A B ∥ C D

, 2.

E F ∥ A B

, 3.

C D ∥ E F

\frac{1}{2} = \frac{2}{4}

Możliwe odpowiedzi: 1.

A B ∥ C D

, 2.

E F ∥ A B

, 3.

C D ∥ E F

\frac{2}{3} = \frac{4}{6}

Możliwe odpowiedzi: 1.

A B ∥ C D

, 2.

E F ∥ A B

, 3.

C D ∥ E F

Przekątne $A C$ i $B D$ czworokąta $A B C D$ przecinają się w punkcie $P$ . Na odcinku $A P$ zaznaczono punkt $E$ , natomiast na odcinku $B D$ punkt $F$ . Znając długości odcinków: $A E = 3$ , $E P = 2$ , $P C = 1$ oraz $B F = 6$ , $F P = 4$ , $P D = 2$ dopasuj proporcję odcinków powstałych na przekątnych do równoległości odpowiednich prostych:

$\frac{1}{5} = \frac{2}{10}$
$\frac{1}{2} = \frac{2}{4}$
$\frac{2}{3} = \frac{4}{6}$

Ćwiczenie 5

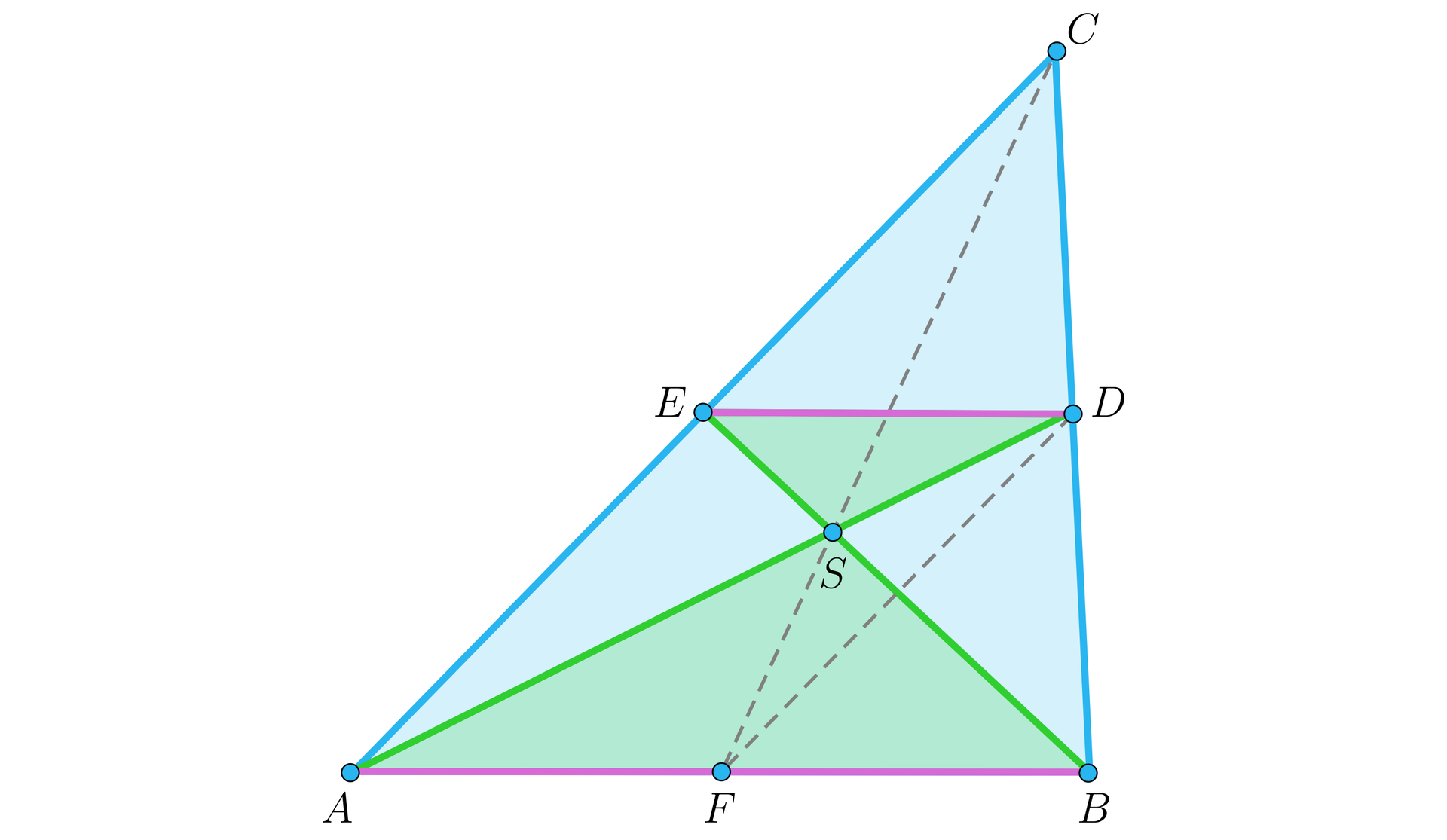
Uzasadnij, że środkowe w trójkącie przecinają się w jednym punkcie i że dzieli on każdą z nich w stosunku $2 : 1$ , licząc od wierzchołka.

R5JPia9MToXcE

Ilustracja przedstawia trójkąt ABC. Na środkach boków umieszczono punkty, na podstawie AB punkt F, na boku AC punkt E, a na boku BC punkt D. Odcinek ED oraz AB są równoległe. Z wierzchołka A oraz B poprowadzono środkowe do punktów przeciwległych, tworząc odcinki AD oraz B E. Odcinki te przecinają się w punkcie S. Następne linią przerywaną zaznaczono środkowe C F oraz F D.

Niech punkt $D$ będzie środkiem boku $B C$ , punkt $E$ środkiem boku $A C$ oraz punkt $S$ punktem przecięcia środkowych $A D$ i $B E$ . Z twierdzenia odwrotnego do twierdzenia Talesa lub z twierdzenia o odcinku łączącym środki boków w trójkącie otrzymujemy, że odcinek $E D$ jest równoległy do $A B$ oraz, że jest dwa razy krótszy od $A B$ . Następnie z podobieństwa trójkątów $ABS$ oraz $EDS$ ( $k k k$ ) dostajemy $\frac{|A B|}{|E D|} = \frac{|A S|}{|S D|} = \frac{|B S|}{|S E|} = \frac{2}{1}$ . Powtarzając rozumowanie dla pary środkowych $A D$ i $C F$ dowodzimy, że punkt przecięcia tych środkowych dzieli je w stosunku $2 : 1$ licząc od wierzchołków. Do dowodu, że są współpękowe wystarczy zauważyć, że na odcinku $A D$ jest tylko jeden punkt, który dzieli ją w stosunku $2 : 1$ licząc od wierzchołka $A$ , stąd wniosek, że środkowe $B E$ i $C F$ przecięły środkową $A D$ tym samym punkcie.

Ćwiczenie 6

Dany jest czworokąt wypukły $A B C D$ , którego przekątne przecinają się w punkcie $P$ . Na przekątnej $A C$ dane są jeszcze dwa punkty $Q$ i $R$ , dzielące ją wraz z punktem $P$ na cztery równe części, tzn. $|A P| = |P Q| = |Q R| = |R C|$ . Na przekątnej $D B$ dane są jeszcze punkty $S$ i $T$ , które wraz z $P$ dzielą ją na cztery równe części, tzn. $|D P| = |P S| = |S T| = |T B|$ (rysunek). Oblicz stosunek pól czworokątów $T R Q S$ i $A B C D$ .

R1XcT3KZAQuv5

Ilustracja przedstawia nieforemny czworokąt ABCD, w którym wykreślono przekątne przecinające się w punkcie P. Na przekątnych AC oraz BD umieszczono punkty będące równoległymi odcinkami Q S oraz RT. Tworzą one trapez STRQ

Z twierdzenia odwrotnego do twierdzenia Talesa wynika, że odcinki $A D$ , $S Q$ , $T R$ i $B C$ są równoległe, więc $S T R Q$ i $A B C D$ są trapezami o stosunku wysokości $1 : 4$ . Ponadto z twierdzenia Talesa lub z podobieństwa trójkątów ( $k k k$ ) dostajemy, że $|A D| : |S Q| : |T R| : |B C| = 1 : 1 : 2 : 3$ . Zatem $\frac{P_{S T R Q}}{P_{A B C D}} = \frac{\frac{1}{2} (a + 2 a) \cdot h}{\frac{1}{2} (a + 3 a) \cdot 4 h} = \frac{3}{16}$ .

Ćwiczenie 7

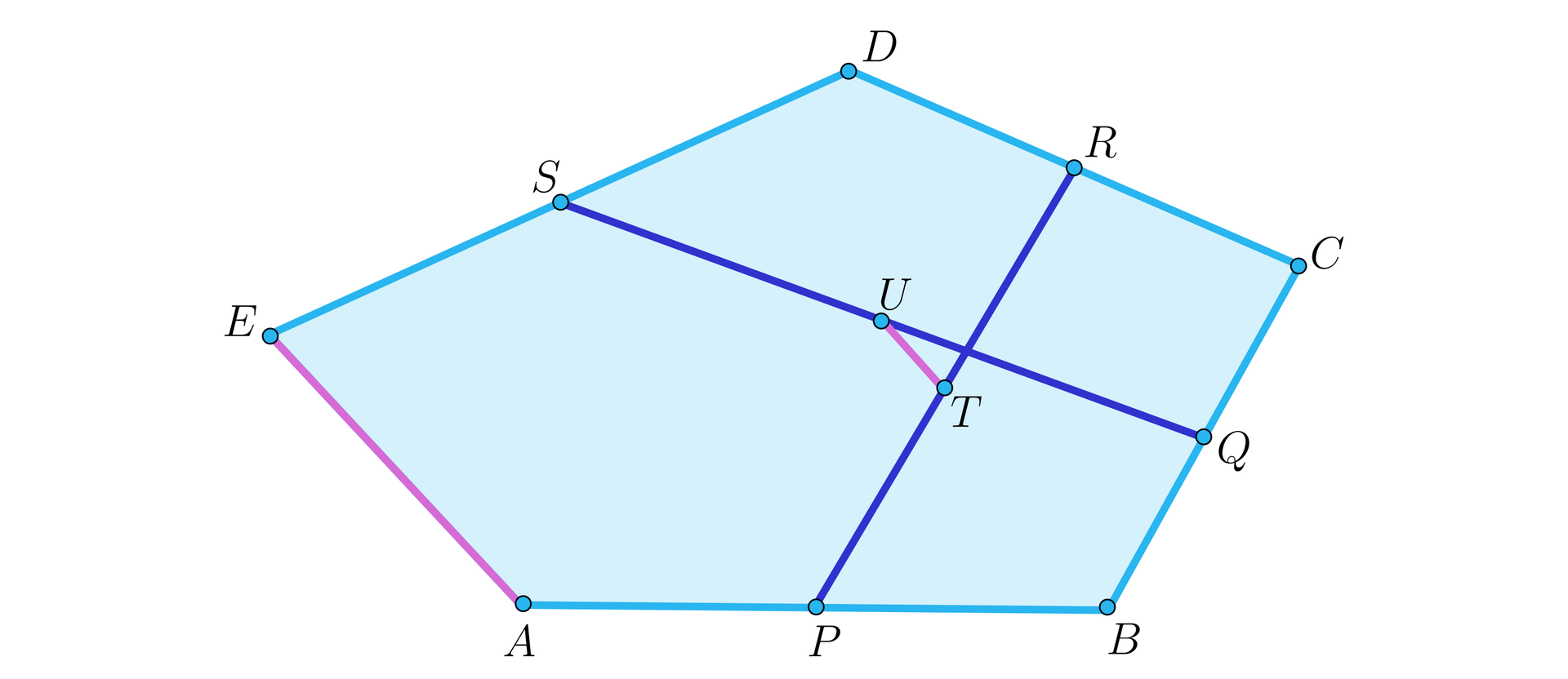
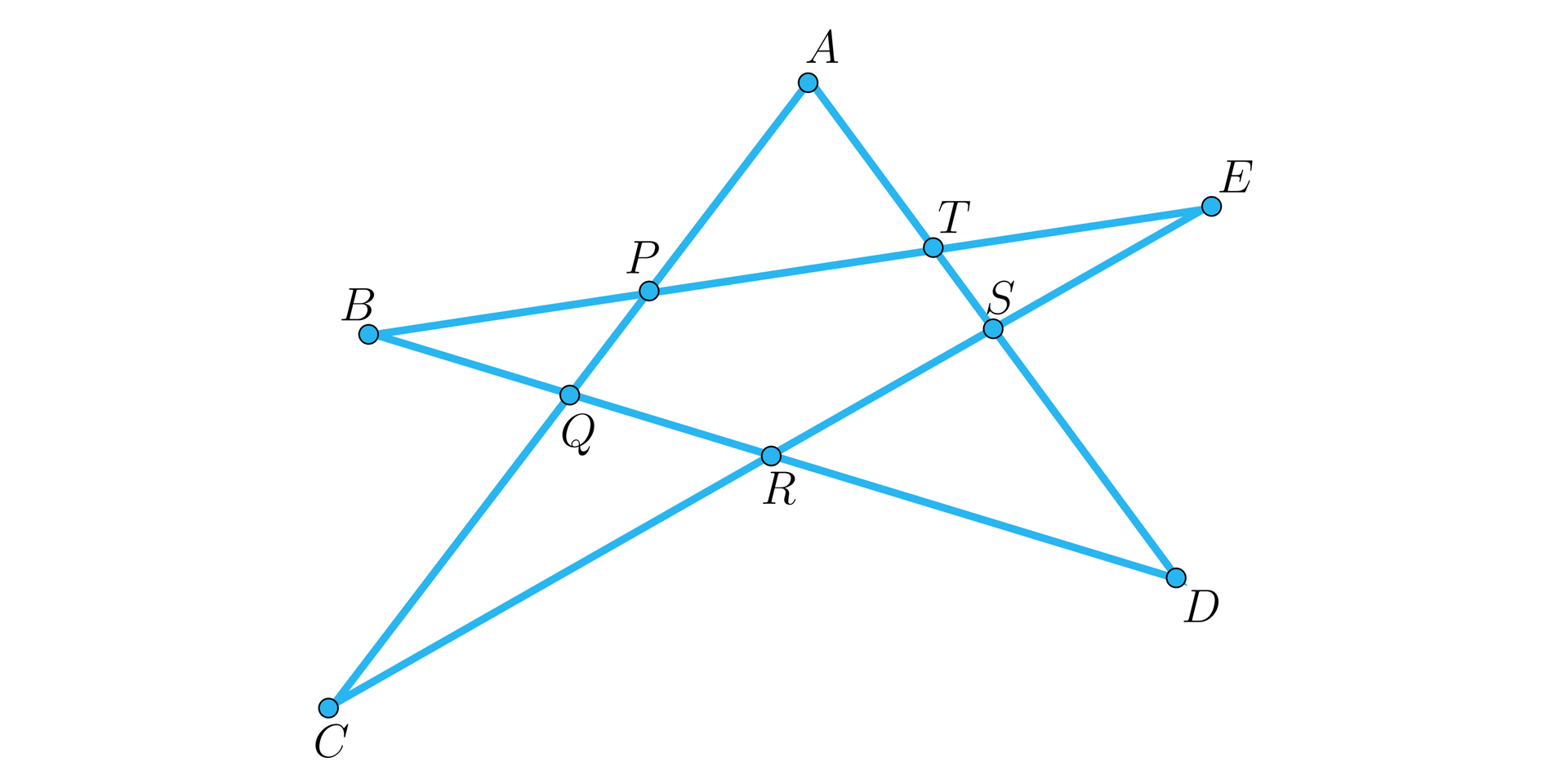
W pięciokącie gwiaździstym $A B C D E$ zachodzą równości $|A Q| = |Q C|$ , $|B R| = |R D|$ , $|C R| = |R E|$ i $|D S| = |S A|$ (rysunek). Uzasadnij, że odcinki $B P$ , $P T$ , $T E$ maja równa długość.

R1UMUdClWBRnf

Ilustracja przedstawia pięciokąt gwiaździsty ABCDE. W jego środku powstał pięciokąt RSTPQ

Rirh6JwiS5gcA

Przeanalizuj i uzupełnij tekst, aby prowadził do poprawnego dowodu. Zauważmy, że odcinki

B D

C E

przecinają się w połowie więc czworokąt

B C D E

jest 1.

R B E

, 2. linią środkową, 3. równoległobokiem, 4.

|E S| = |S R|

, 5. równoległy, 6.

\frac{|E S|}{|S C|} = \frac{|E T|}{|C D|} = \frac{1}{3}

, 7.

B E

, 8.

Q S

. Ponadto odcinek 1.

R B E

, 2. linią środkową, 3. równoległobokiem, 4.

|E S| = |S R|

, 5. równoległy, 6.

\frac{|E S|}{|S C|} = \frac{|E T|}{|C D|} = \frac{1}{3}

, 7.

B E

, 8.

Q S

jest linią środkową w trójkącie

A C D

. Jest więc 1.

R B E

, 2. linią środkową, 3. równoległobokiem, 4.

|E S| = |S R|

, 5. równoległy, 6.

\frac{|E S|}{|S C|} = \frac{|E T|}{|C D|} = \frac{1}{3}

, 7.

B E

, 8.

Q S

do odcinka

C D

oraz 1.

R B E

, 2. linią środkową, 3. równoległobokiem, 4.

|E S| = |S R|

, 5. równoległy, 6.

\frac{|E S|}{|S C|} = \frac{|E T|}{|C D|} = \frac{1}{3}

, 7.

B E

, 8.

Q S

i jego długość to połowa

C D

jak i odcinka

B E

. Z tego wynika, że odcinek

Q S

jest też 1.

R B E

, 2. linią środkową, 3. równoległobokiem, 4.

|E S| = |S R|

, 5. równoległy, 6.

\frac{|E S|}{|S C|} = \frac{|E T|}{|C D|} = \frac{1}{3}

, 7.

B E

, 8.

Q S

w trójkącie 1.

R B E

, 2. linią środkową, 3. równoległobokiem, 4.

|E S| = |S R|

, 5. równoległy, 6.

\frac{|E S|}{|S C|} = \frac{|E T|}{|C D|} = \frac{1}{3}

, 7.

B E

, 8.

Q S

. To oznacza, że

|B Q| = |Q R|

oraz 1.

R B E

, 2. linią środkową, 3. równoległobokiem, 4.

|E S| = |S R|

, 5. równoległy, 6.

\frac{|E S|}{|S C|} = \frac{|E T|}{|C D|} = \frac{1}{3}

, 7.

B E

, 8.

Q S

. Z podobieństwa trójkątów wynika, że

\frac{|B Q|}{|Q D|} = \frac{|B P|}{|D C|} = \frac{1}{3}

oraz, że 1.

R B E

, 2. linią środkową, 3. równoległobokiem, 4.

|E S| = |S R|

, 5. równoległy, 6.

\frac{|E S|}{|S C|} = \frac{|E T|}{|C D|} = \frac{1}{3}

, 7.

B E

, 8.

Q S

a zatem

|B P| = |T E| = |P T| = \frac{1}{3} |B E|

co należało udowodnić.

Przeanalizuj i uzupełnij tekst, aby prowadził do poprawnego dowodu.

$B E$ , $\frac{E S}{S C} = \frac{E T}{C D} = \frac{1}{3}$ , $E S = S R$ , równoległobokiem, równoległy, linią środkową, $R B E$ , $Q S$

Zauważmy, że odcinki $B D$ i $C E$ przecinają się w połowie więc czworokąt $B C D E$ jest ..................................... Ponadto odcinek .................................... jest linią środkową w trójkącie $A C D$ . Jest więc .................................... do odcinka $C D$ oraz .................................... i jego długość to połowa $C D$ jak i odcinka $B E$ . Z tego wynika, że odcinek $Q S$ jest też .................................... w trójkącie ..................................... To oznacza, że $B Q = Q R$ oraz ..................................... Z podobieństwa trójkątów wynika, że $\frac{B Q}{Q D} = \frac{B P}{D C} = \frac{1}{3}$ oraz, że .................................... a zatem $B P = T E = P T = \frac{1}{3} B E$ co należało udowodnić.

Ćwiczenie 8

Środki boków $A B$ i $C D$ oraz $B C$ i $D E$ pięciokąta wypukłego $A B C D E$ połączono odcinkami $P R$ i $S Q$ , których środki również połączono odcinkiem $U T$ (rysunek). Udowodnij, że odcinek ten jest równoległy do boku $A E$ i równy $\frac{1}{4} |A E|$ .

R1dRtbfZat64l

Ilustracja przedstawia pięciokąt wypukły ABCDE. Środki boków AB I CD oraz BC i DE połączono odcinkami PR I SQ których środki również połączono odcinkiem UT.

Poprowadźmy jeszcze przekątną $B E$ i oznaczmy jej środek przez $W$ . Stosując kilka razy twierdzenie odwrotne do twierdzenia Talesa lub twierdzenie o odcinku łączącym środki ramion otrzymujemy, że czworokąt $W Q R S$ jest równoległobokiem, którego przekątne $W R$ i $Q S$ połowią się w punkcie $U$ . Z twierdzenia odwrotnego do twierdzenia Talesa otrzymujemy równoległość $U T$ i $W P$ oraz równoległość odcinków $W P$ i $A E$ , co daje równoległość $U T$ i $A E$ . Ponadto wiemy, że $|U T| = \frac{1}{2} |W P| = \frac{1}{2} \cdot \frac{1}{2} |A E| = \frac{1}{4} |A E|$ co jest równoważne z tezą ćwiczenia.

RdTfchZ3Jlgic

Galeria zdjęć interaktywnych

Dla nauczyciela