Galeria zdjęć interaktywnych
Polecenie 1
Oglądając galerię zdjęć interaktywnych, spróbuj najpierw samodzielnie rozwiązać zamieszczone tam zadania, a dopiero następnie porównaj rozwiązania.
Zapoznaj się z galerią zdjęć interaktywnych, spróbuj najpierw samodzielnie rozwiązać zamieszczone tam zadania, a dopiero następnie porównaj rozwiązania.
Ilustracja pierwsza przedstawia przykład pierwszy, którego celem jest obliczenie pola powierzchni ostrosłupa prawidłowego sześciokątnego. Do obliczenia pola powierzchni ostrosłupa prawidłowego sześciokątnego potrzebujemy wysokość ściany bocznej oraz długość krawędzi podstawy. Poniżej treści znajduje się następujący rysunek: na rysunku znajduje się ostrosłup prawidłowy sześciokątny, w którym zaznaczono trójkąt prostokątny składający się z wysokości ostrosłupa H, która jest przyprostokątną, krawędzi ściany bocznej, która jest przeciw prostokątną oraz drugiej przyprostokątnej leżącej w płaszczyźnie podstawy. Kąt pomiędzy przeciwprostokątną a przyprostokątną leżącą w płaszczyźnie podstawy ma 45 stopni.
Ilustracja pierwsza przedstawia przykład pierwszy, którego celem jest obliczenie pola powierzchni ostrosłupa prawidłowego sześciokątnego. Do obliczenia pola powierzchni ostrosłupa prawidłowego sześciokątnego potrzebujemy wysokość ściany bocznej oraz długość krawędzi podstawy. Poniżej treści znajduje się następujący rysunek: na rysunku znajduje się ostrosłup prawidłowy sześciokątny, w którym zaznaczono trójkąt prostokątny składający się z wysokości ostrosłupa H, która jest przyprostokątną, krawędzi ściany bocznej, która jest przeciw prostokątną oraz drugiej przyprostokątnej leżącej w płaszczyźnie podstawy. Kąt pomiędzy przeciwprostokątną a przyprostokątną leżącą w płaszczyźnie podstawy ma 45 stopni.Ilustracja druga zawiera kontynuację przykładu pierwszego. Zatem oznaczmy jako a krawędź podstawy. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 45 stopni, zatem , a krawędź boczna ma miarę . Narysujmy ścianę boczną ostrosłupa. Ściana boczna jest trójkątem równoramiennym, podstawa jes podpisana literą H, a ramiona są podpisane , wysokość w tym trójkącie opuszczoną na podstawę podpisano małe h. Wykorzystując twierdzenie Pitagorasa obliczamy wysokość trójkąta. Wówczas , zatem , czyli .
Ilustracja druga zawiera kontynuację przykładu pierwszego. Zatem oznaczmy jako a krawędź podstawy. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 45 stopni, zatem , a krawędź boczna ma miarę . Narysujmy ścianę boczną ostrosłupa. Ściana boczna jest trójkątem równoramiennym, podstawa jes podpisana literą H, a ramiona są podpisane , wysokość w tym trójkącie opuszczoną na podstawę podpisano małe h. Wykorzystując twierdzenie Pitagorasa obliczamy wysokość trójkąta. Wówczas , zatem , czyli .Ilustracja trzecia zawiera kontynuację przykładu pierwszego. Teraz obliczamy pole powierzchni całkowitej naszego ostrosłupa, który prezentował się następująco: ostrosłup prawidłowy sześciokątny, w którym zaznaczono trójkąt prostokątny składający się z wysokości ostrosłupa H, która jest przyprostokątną, krawędzi ściany bocznej, która jest przeciw prostokątną oraz drugiej przyprostokątnej leżącej w płaszczyźnie podstawy. Kąt pomiędzy przeciwprostokątną a przyprostokątną leżącą w płaszczyźnie podstawy ma 45 stopni. Najpierw zauważ, że nasz sześciokąt foremny ma krawędź długości , zatem . Pole powierzchni bocznej możesz policzyć ze wzoru , gdzie - krawędź podstawy, – wysokość ściany bocznej. Czyli otrzymujemy . Pole powierzchni całkowitej to pole podstawy plus pole powierzchni bocznej, zatem .
Ilustracja trzecia zawiera kontynuację przykładu pierwszego. Teraz obliczamy pole powierzchni całkowitej naszego ostrosłupa, który prezentował się następująco: ostrosłup prawidłowy sześciokątny, w którym zaznaczono trójkąt prostokątny składający się z wysokości ostrosłupa H, która jest przyprostokątną, krawędzi ściany bocznej, która jest przeciw prostokątną oraz drugiej przyprostokątnej leżącej w płaszczyźnie podstawy. Kąt pomiędzy przeciwprostokątną a przyprostokątną leżącą w płaszczyźnie podstawy ma 45 stopni. Najpierw zauważ, że nasz sześciokąt foremny ma krawędź długości , zatem . Pole powierzchni bocznej możesz policzyć ze wzoru , gdzie - krawędź podstawy, – wysokość ściany bocznej. Czyli otrzymujemy . Pole powierzchni całkowitej to pole podstawy plus pole powierzchni bocznej, zatem .Ilustracja czwarta zawiera przykład drugi o treści: Obliczmy pole powierzchni następującego ostrosłupa prawidłowego sześciokątnego: dany jest ostrosłup prawidłowy sześciokątny, w którym zaznaczono trójkąt prostokątny składający się z wysokości ostrosłupa, która jest przyprostokątną, wysokości ściany bocznej h, która jest przeciw prostokątną oraz drugiej przyprostokątnej łączącej spodki tych wysokości. Kąt pomiędzy wysokością ostrosłupa a podstawą to kąt prosty, kąt pomiędzy wysokością ściany bocznej a krawędzią boczną to również kąt prosty. Kąt pomiędzy wysokościami ma 30 stopni. Do obliczenia pola powierzchni ostrosłupa prawidłowego sześciokątnego potrzebujemy wysokość ściany bocznej oraz długość krawędzi podstawy.
Ilustracja czwarta zawiera przykład drugi o treści: Obliczmy pole powierzchni następującego ostrosłupa prawidłowego sześciokątnego: dany jest ostrosłup prawidłowy sześciokątny, w którym zaznaczono trójkąt prostokątny składający się z wysokości ostrosłupa, która jest przyprostokątną, wysokości ściany bocznej h, która jest przeciw prostokątną oraz drugiej przyprostokątnej łączącej spodki tych wysokości. Kąt pomiędzy wysokością ostrosłupa a podstawą to kąt prosty, kąt pomiędzy wysokością ściany bocznej a krawędzią boczną to również kąt prosty. Kąt pomiędzy wysokościami ma 30 stopni. Do obliczenia pola powierzchni ostrosłupa prawidłowego sześciokątnego potrzebujemy wysokość ściany bocznej oraz długość krawędzi podstawy.Ilustracja piąta przedstawia kontynuację przykładu drugiego. Zauważmy, że wysokość ściany bocznej jest nachylona do wysokości ostrosłupa pod kątem trzydziestu stopni, zatem . Wyrysujmy ten trójkąt. Trójkąt składa się z przeciwprostokątnej podpisanej małe h, przyprostokątnej podpisanej literą x i przyprostokątnej podpisanej . Kąt pomiędzy przyprostokątną a przeciwprostokątną wynosi 30 stopni. Wiemy, że odcinek x to połowa krótszej przekątnej podstawy. Zatem krawędź podstawy ma długość , czyli , zatem . Wystarczy przekształcić wzór .
Ilustracja piąta przedstawia kontynuację przykładu drugiego. Zauważmy, że wysokość ściany bocznej jest nachylona do wysokości ostrosłupa pod kątem trzydziestu stopni, zatem . Wyrysujmy ten trójkąt. Trójkąt składa się z przeciwprostokątnej podpisanej małe h, przyprostokątnej podpisanej literą x i przyprostokątnej podpisanej . Kąt pomiędzy przyprostokątną a przeciwprostokątną wynosi 30 stopni. Wiemy, że odcinek x to połowa krótszej przekątnej podstawy. Zatem krawędź podstawy ma długość , czyli , zatem . Wystarczy przekształcić wzór .Ilustracja szósta zawiera kontynuację przykładu drugiego, teraz obliczymy pole powierzchni ostrosłupa prawidłowego sześciokątnego takiego, że dany jest ostrosłup prawidłowy sześciokątny, w którym zaznaczono trójkąt prostokątny składający się z wysokości ostrosłupa, która jest przyprostokątną, wysokości ściany bocznej h, która jest przeciw prostokątną oraz drugiej przyprostokątnej łączącej spodki tych wysokości. Kąt pomiędzy wysokością ostrosłupa a podstawą to kąt prosty, kąt pomiędzy wysokością ściany bocznej a krawędzią boczną to również kąt prosty. Kąt pomiędzy wysokościami ma 30 stopni. Podstawa sześciokąta foremnego ma długość . Zatem mamy . Z kolei pole powierzchni bocznej to suma pól ścian bocznych ostrosłupa, którą obliczamy następująco: . Ostatecznie dodajmy pole podstawy do pola bocznego i otrzymujemy .
Ilustracja szósta zawiera kontynuację przykładu drugiego, teraz obliczymy pole powierzchni ostrosłupa prawidłowego sześciokątnego takiego, że dany jest ostrosłup prawidłowy sześciokątny, w którym zaznaczono trójkąt prostokątny składający się z wysokości ostrosłupa, która jest przyprostokątną, wysokości ściany bocznej h, która jest przeciw prostokątną oraz drugiej przyprostokątnej łączącej spodki tych wysokości. Kąt pomiędzy wysokością ostrosłupa a podstawą to kąt prosty, kąt pomiędzy wysokością ściany bocznej a krawędzią boczną to również kąt prosty. Kąt pomiędzy wysokościami ma 30 stopni. Podstawa sześciokąta foremnego ma długość . Zatem mamy . Z kolei pole powierzchni bocznej to suma pól ścian bocznych ostrosłupa, którą obliczamy następująco: . Ostatecznie dodajmy pole podstawy do pola bocznego i otrzymujemy .Polecenie 2
Obliczmy pole powierzchni całkowitej ostrosłupa prawidłowego przedstawionego na rysunku.
Ilustracja przedstawia ostrosłup prawidłowy sześciokątny, w którym zaznaczono trójkąt prostokątny składający się z wysokości ostrosłupa H, która jest przyprostokątną, krawędzi ściany bocznej, która jest przeciw prostokątną oraz drugiej przyprostokątnej leżącej w płaszczyźnie podstawy. Kąt pomiędzy przeciwprostokątną a przyprostokątną leżącą w płaszczyźnie podstawy ma 60 stopni.
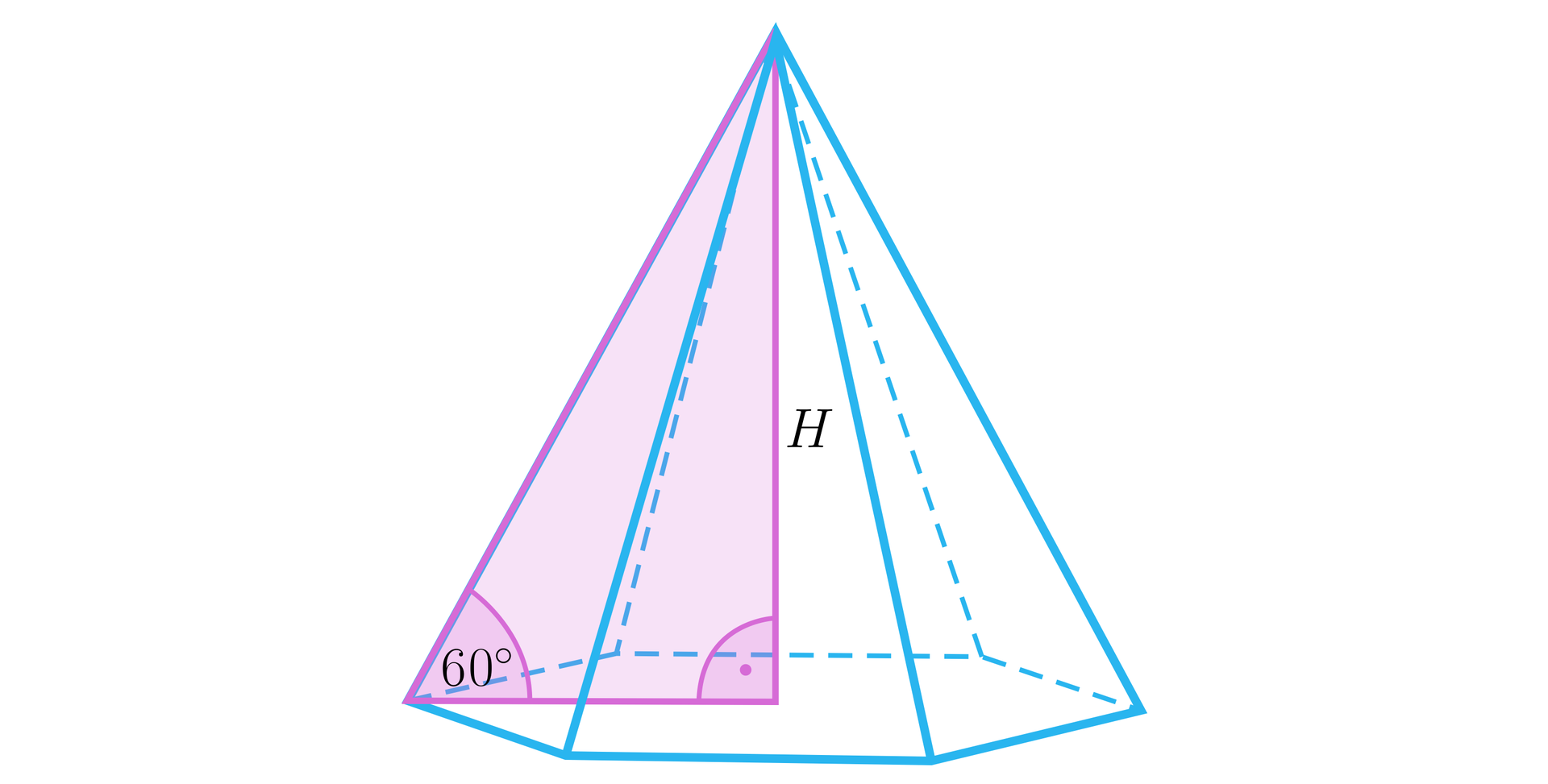
Niech – długość krawędzi podstawy. Wówczas .
Długość krawędzi bocznej zaś wynosi .
Narysujmy ścianę boczną ostrosłupa.
Ilustracja przedstawia trójkąt, którego podstawa ma długość , a ramiona mają długość . Wysokość jest pod kątem prostym do podstawy.
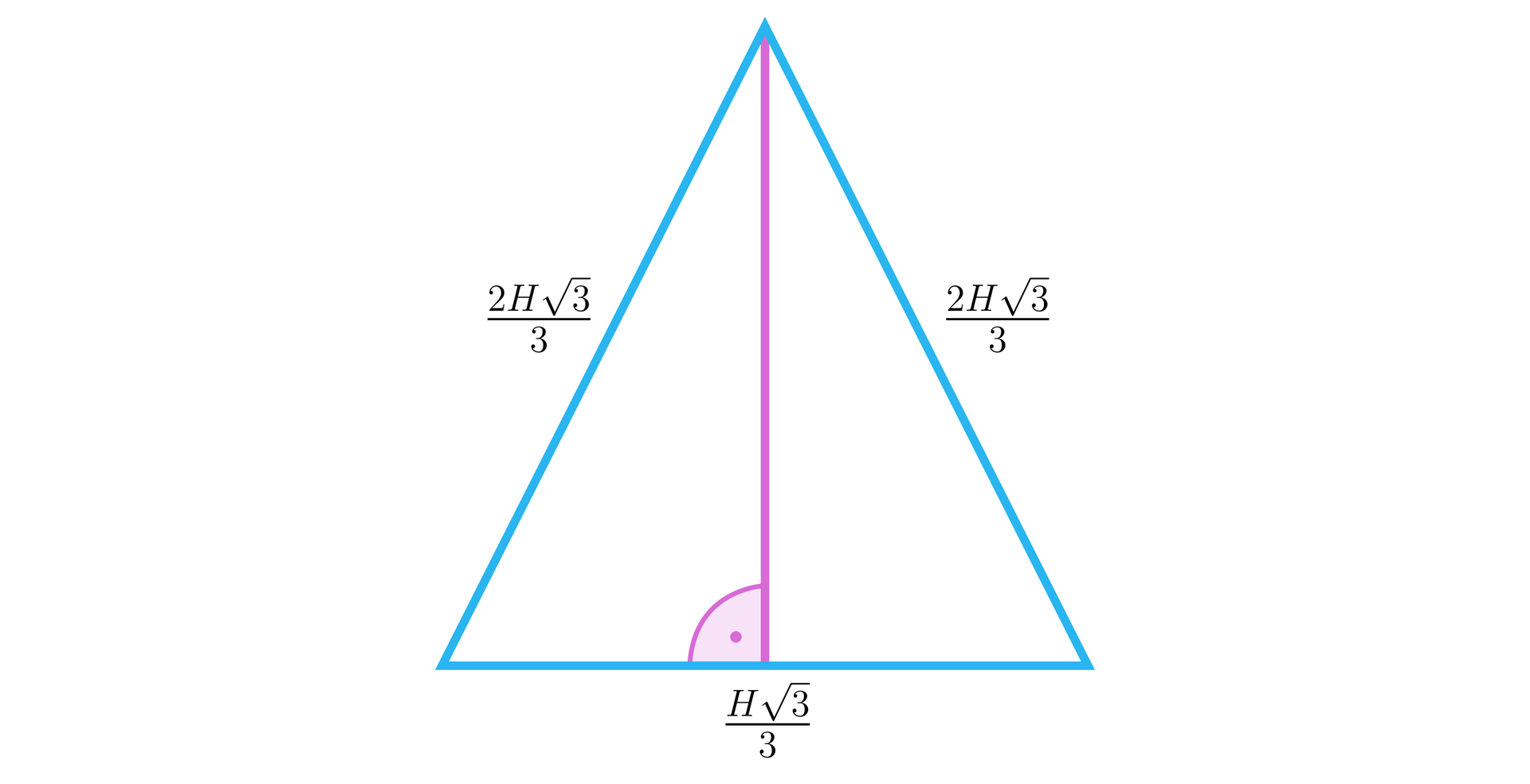
Obliczmy wysokość ściany bocznej:
,
,
,
.
Możemy więc obliczyć pole powierzchni całkowitej ostrosłupa:
,
,
.