Galeria zdjęć interaktywnych

Polecenie 1

Zapoznaj się z galerią zdjęć interaktywnych, a następnie wykonaj poniższe polecenie.

RSYZ71uFFlu8P

R1Y5iwXS5FToc

RLsdJzW6DCU2l

RuNQdq7vX3gJh

RE4PiHNUD0fl3

Polecenie 2

Prostokąt $F_{1}$ o przekątnej długości $2 \sqrt{10}$ jest podobny do prostokąta $F_{2}$ o bokach długości $2$ i $1$ . Oblicz stosunek pola prostokąta $F_{2}$ do pola prostokąta $F_{1}$ .

Narysujmy dwa prostokąty podobne i wprowadźmy odpowiednie oznaczenia.

RLugH01ynqoIh

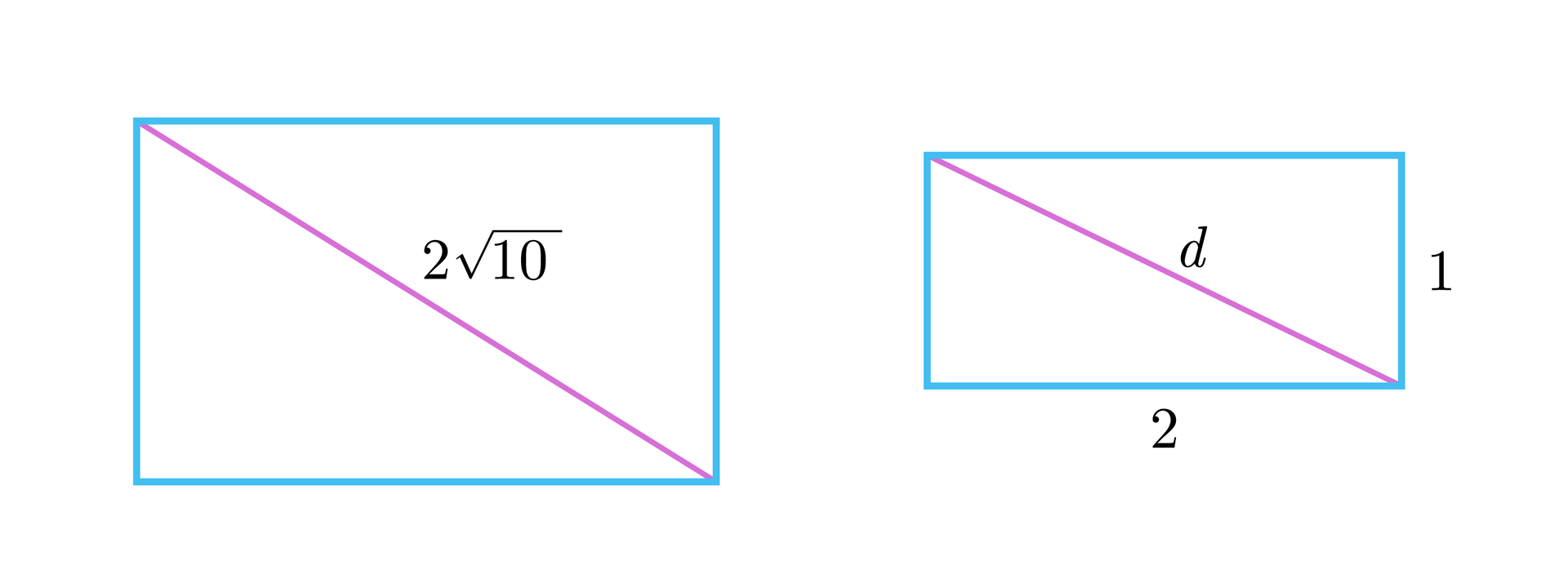
Ilustracja przedstawia dwa prostokąty. Jeden o przekątnej długości 210 oraz drugi o bokach długości 2 i 1 oraz przekątnej długości d.

Jeżeli $d$ jest długością przekątnej prostokąta $F_{2}$ , to do wyznaczenia wartości $d$ stosujemy twierdzenie Pitagorasa:

$2^{2} + 1^{2} = d^{2} \Rightarrow d = \sqrt{5}$

Wobec tego skala $k$ podobieństwa prostokąta $F_{2}$ do prostokąta $F_{1}$ wynosi:

$k = \frac{\sqrt{5}}{2 \sqrt{10}} = \frac{1}{2 \sqrt{2}} = \frac{\sqrt{2}}{4}$

Zatem stosunek pola prostokąta $F_{2}$ do pola prostokąta $F_{1}$ wynosi:

$k^{2} = {(\frac{\sqrt{2}}{4})}^{2} = \frac{2}{16} = \frac{1}{8}$ .

Przeczytaj

Sprawdź się