Przekształcenie geometryczne, które zachowuje stosunek odległości punktów, nazywamy podobieństwem.

Jeżeli figury $F_1$ i $F_2$ o polach odpowiednio $P_1$ i $P_2$ są podobne w skali $k$, to zachodzi następująca zależność:

Trójkąt równoboczny $F_1$ jest podobny do trójkąta równobocznego $F_2$ w skali $k=\frac{4}{7}$. Wyznaczymy obwody tych trójkątów i pole trójkąta $F_2$, jeżeli pole trójkąta $F_1$ jest równe $16\sqrt{3}$.

Rozwiązanie:

Niech $P_1$ będzie polem trójkąta $F_1$, a $P_2$ – polem trójkąta $F_2$.

Korzystając z faktu, że stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa, otrzymujemy zależność:

$\frac{P_1}{P_2}={\left(\frac{4}{7}\right)}^2$

$\frac{16\sqrt{3}}{P_2}=\frac{16}{49}$

$P_2=\frac{16\sqrt{3}·49}{16}=49\sqrt{3}$

Niech $a$ będzie długością boku trójkąta $F_2$.

Wówczas:

$\frac{a^2\sqrt{3}}{4}=49\sqrt{3}$

$a^2\sqrt{3}=196\sqrt{3}$

$a^2=196\Rightarrow a=\sqrt{196}=14$

Zatem obwód $L_2$ trójkąta $F_2$ wynosi:

$L_2=3·14=42$

Do wyznaczenia obwodu $L_1$ trójkąta $F_1$ wykorzystujemy zależność:

$\frac{L_1}{L_2}=\frac{4}{7}$

Zatem:

$\frac{L_1}{42}=\frac{4}{7}\Rightarrow L_1=24$.

Obwody czterech czworokątów $L_1$, $L_2$, $L_3$, $L_4$ są kolejnymi wyrazami ciągu geometrycznego o ilorazie równym $\frac{2}{5}$. Obliczymy obwody i pola tych figur, jeżeli suma ich obwodów wynosi $406$, a pole czworokąta o obwodzie $L_1$ wynosi $50$.

Rozwiązanie:

Z treści zadania wynika zależność:

$L_1+L_2+L_3+L_4=406$

Ponieważ liczby te są kolejnymi wyrazami ciągu geometrycznego o ilorazie równym $\frac{2}{5}$, to zachodzi następująca zależność:

$L_1+\frac{2}{5}·L_1+\frac{4}{25}·L_1+\frac{8}{125}·L_1=406$

$\frac{203}{125}·L_1=406\Rightarrow L_1=406·\frac{125}{203}=250$

Zatem

$L_2=\frac{2}{5}·250=100$

$L_3=\frac{4}{25}·250=40$

$L_4=\frac{8}{125}·250=16$

Zauważmy, że:

$P_1=50$

$\frac{L_2}{L_1}=\frac{2}{5}\Rightarrow \frac{P_2}{P_1}=\frac{4}{25}\Rightarrow P_2=\frac{4}{25}·50=8$

$\frac{P_3}{P_2}=\frac{4}{25}\Rightarrow P_3=\frac{4}{25}·8=\frac{32}{25}$

$\frac{P_4}{P_3}=\frac{4}{25}\Rightarrow P_4=\frac{4}{25}·\frac{32}{25}=\frac{128}{625}$.

Dany jest trapez równoramienny $ABCD$ o podstawach długości $\left|AB\right|=4a$ i $\left|CD\right|=a$, gdzie $a>0$. Wykażemy, że jeśli punkt $S$ jest punktem przecięcia przekątnych tego trapezu to $\frac{P_{ABS}}{P_{CDS}}=16$.

Rozwiązanie:

Narysujmy rysunek pomocniczy do zadania i wprowadźmy odpowiednie oznaczenia:

R1GwGNTaiO9KC

Ilustracja przedstawia trapez ABCD o wysokości FE upuszczonej na środek dłuższej podstawy AB. Zaznaczono przekątne przecinające się w punkcie S i dzielące wysokość na dwie długości x i y.

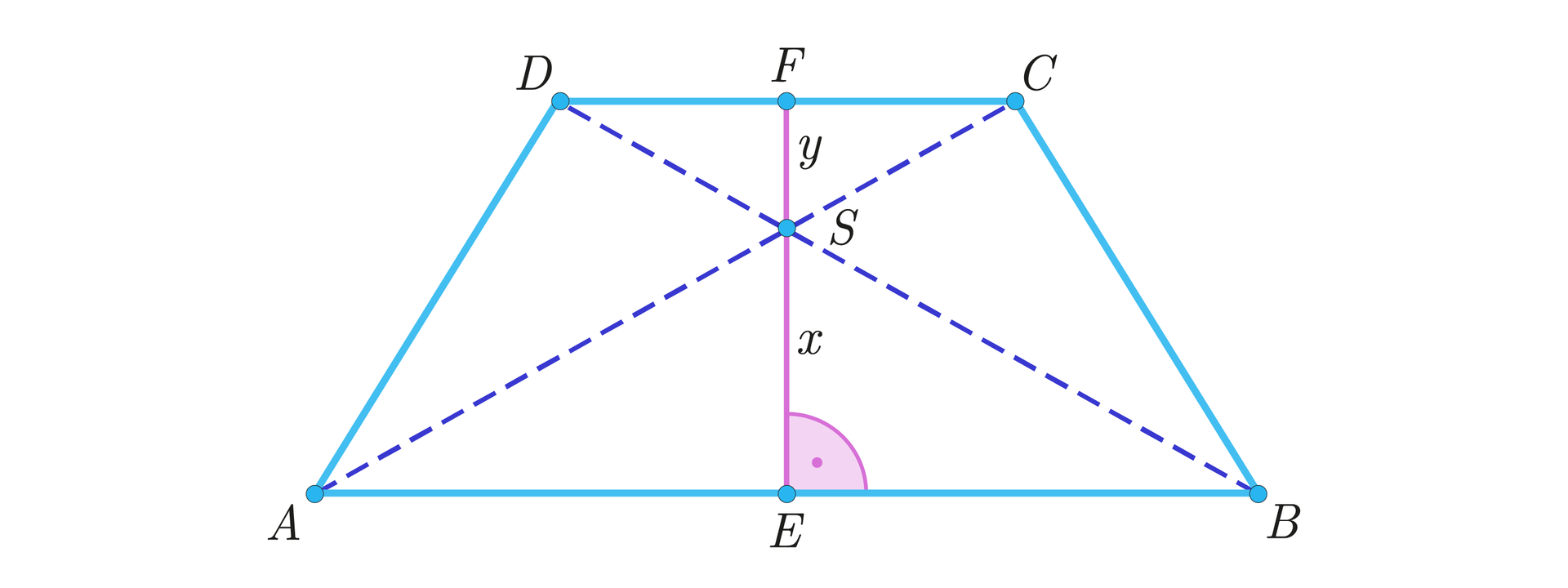
Ponieważ $AB\parallel CD$, zatem   z własności kątów przy prostych równoległych:

$\left|\sphericalangle SAB\right|=\left|\sphericalangle SCD\right|$ oraz $\left|\sphericalangle ABS\right|=\left|\sphericalangle SDC\right|$

Dodatkowo  z własności kątów  wierzchołkowych: $\left|\sphericalangle ASB\right|=\left|\sphericalangle CSD\right|$

Wobec tego trójkąty $ABS$ i $CDS$ są podobne na podstawie cechy podobieństwa $kkk$.

Jeżeli $\left|AB\right|=4a$ i $\left|CD\right|=a$, to:

$\frac{x}{y}=\frac{4a}{a}=4$

Czyli $x=4y$.

Zatem:

$\frac{P_{ABS}}{P_{CDS}}=\frac{{\displaystyle \frac{1}{2}·4a·x}}{{\displaystyle \frac{1}{2}·a·y}}=\frac{2ax}{{\displaystyle \frac{1}{2}ay}}=\frac{2·4y}{{\displaystyle \frac{1}{2}y}}=16$.

Pole powierzchni Polski wynosi około $312679 {\mathrm{km}}^2$. Wyznaczymy pole obszaru  odpowiadającego  polu powierzchni Polski,  znajdującego się na mapie wykonanej w skali $1:3000000$.

Rozwiązanie:

Niech $P_1=312679 {\mathrm{km}}^2$

$P_2$ – pole obszaru, odpowiadającego polu powierzchni Polski, na mapie wykonanej w skali $k=1:3000000$.

Wobec tego:

$\frac{P_2}{312679}=\frac{1}{9000000000000}$

Zatem:

$P_2=\frac{312679}{9000000000000} {\mathrm{k}\mathrm{m}}^2\approx 0,0000000347 {\mathrm{k}\mathrm{m}}^2$

Pole obszaru odpowiadającego  polu powierzchni Polski na mapie wykonanej w skali $k=1:3000000$ wynosi około $0,0000000347 {\mathrm{km}}^2$.

Wiadomo, że suma pól dwóch figur podobnych wynosi $S$. Obliczymy pola tych figur, jeżeli wiadomo, że  skala podobieństwa tych figur wynosi $\frac{1}{5}$.

Rozwiązanie:

Niech $P_1$ i $P_2$ będą polami dwóch figur podobnych.

Do wyznaczenia wartości $P_1$ i $P_2$ rozwiązujemy układ równań:

$\left\{\begin{array}{l}{P}_1+P_2=S\\ \frac{P_1}{P_2}={\left(\frac{1}{5}\right)}^2\end{array}\right.$

Układ równań przekształcamy do postaci:

$\left\{\begin{array}{l}{P}_1+P_2=S\\ P_1=\frac{1}{25}·P_2\end{array}\right.$

Wobec tego:

$\frac{1}{25}{P}_2+P_2=S$

$\frac{26}{25}{P}_2=\mathrm{S}$

$P_2=S·\frac{25}{26}=\frac{25}{26}S$

Zatem:

$P_1=S-\frac{25}{26}S=\frac{1}{26}S$

Pola tych figur wynoszą odpowiednio $\frac{1}{26}S$ i $\frac{25}{26}S$.

Trapez prostokątny o podstawach długości $a$ i $2a$ oraz krótszym ramieniu równym $a$ podzielono odcinkiem równoległym do podstaw na dwa trapezy podobne. Wyznaczymy pola tych trapezów, jeżeli pole trapezu przed podziałem wynosi $12$.

Rozwiązanie:

Narysujmy trapez prostokątny $ABCD$ i wprowadźmy oznaczenia, jak na rysunku.

R1OrLFBltp2Tf

Ilustracja przedstawia trapez ABCD zbudowany z dwóch figur. Kwadratu o boku długości a oraz trójkącie prostokątnym o przyprostokątnych długości a. Na trapezie zaznaczono odcinek EF łączący boki AD i CB.

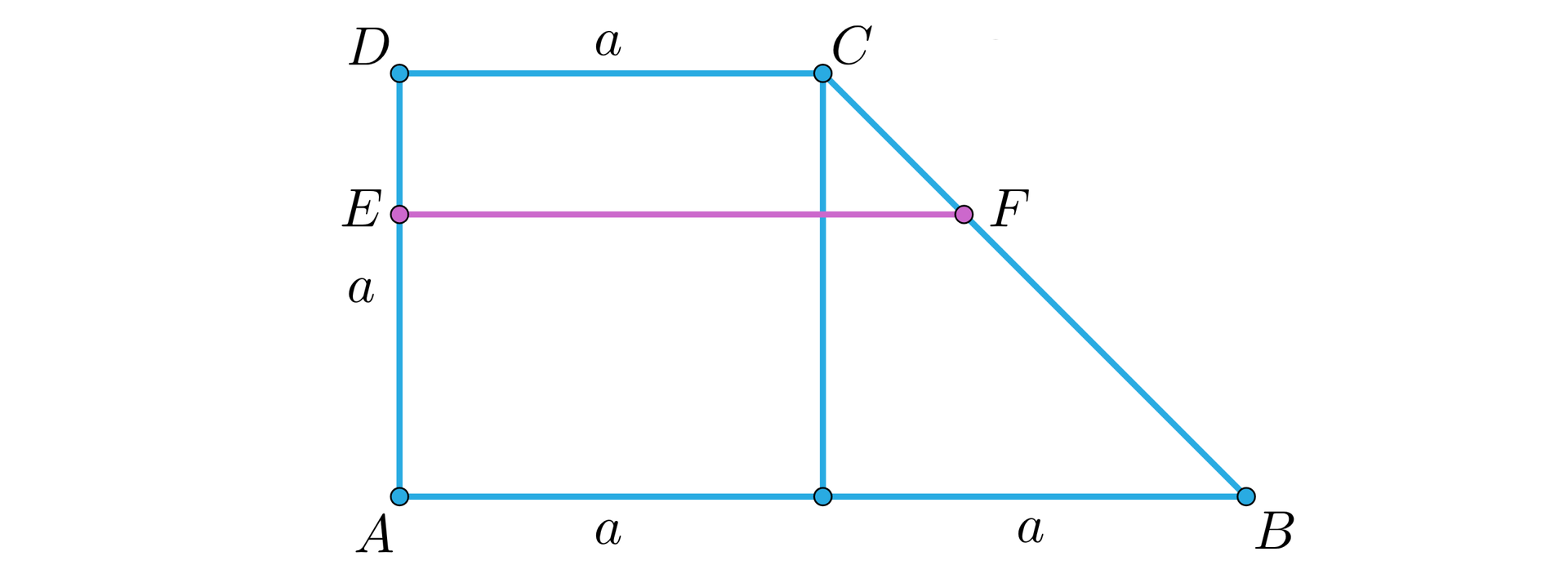
Ponieważ trapezy $ABFE$ i $EFCD$ są podobne, zatem zachodzi następująca zależność:

$\frac{2a}{\left|EF\right|}=\frac{\left|EF\right|}{a}$

Wobec tego ${\left|EF\right|}^2=2a^2$, czyli $\left|EF\right|=a\sqrt{2}$.

Skala $k$ podobieństwa trapezów $ABFE$ i $EFCD$ wynosi:

$k=\frac{2a}{a\sqrt{2}}=\sqrt{2}$

Jeżeli $P_1$ oraz $P_2$ są odpowiednio polami trapezów $ABFE$ i $EFCD$, to:

$\frac{P_1}{P_2}={\left(\sqrt{2}\right)}^2=2$

$P_1=2P_2$

Obliczamy pole trapezu $ABCD$:

$P=\frac{{\displaystyle 2a+a}}{{\displaystyle 2}}·a=\frac{{\displaystyle 3a^2}}{{\displaystyle 2}}$

Ponieważ $P=12$, zatem:

$\frac{{\displaystyle 3a^2}}{2}=12$

$a^2=8\Rightarrow a=2\sqrt{2}$

Wobec tego pola trapezów $ABFE$ i $EFCD$ wynoszą:

$P_2=\frac{P}{3}=\frac{{\displaystyle \frac{3a^2}{2}}}{3}=\frac{a^2}{2}$

$P_2=\frac{a^2}{2}=\frac{{\left(2\sqrt{2}\right)}^2}{2}=\frac{8}{2}=4$

$P_1=2·P_2=2·4=8$

Uwaga - spróbuj pola trapezów z powyższego przykładu wyznaczyć, bez obliczania długości boku a.

Dany jest równoległobok $R_1$, którego boki mają długości $a$ i $b$, gdzie $a>b$, a kąt między tymi bokami ma miarę $\alpha$. Równoległobok $R_2$ o polu równym $P$ jest podobny do równoległoboku $R_1$. Obliczymy obwód równoległoboku $R_2$.

Rozwiązanie:

Narysujmy równoległoboki $R_1$ i $R_2$, które są podobne oraz wprowadźmy oznaczenia, jak na rysunkach.

RvZKICcKDAzUo

Ilustracja przedstawia dwa równoległoboki o kącie wewnętrznym o mierze alfa. Równoległobok R indeks dolny 1 koniec indeksu ma ramiona o długości a i b, równoległobok R indeks dolny 2 koniec indeksu ma ramiona o długości x i y.

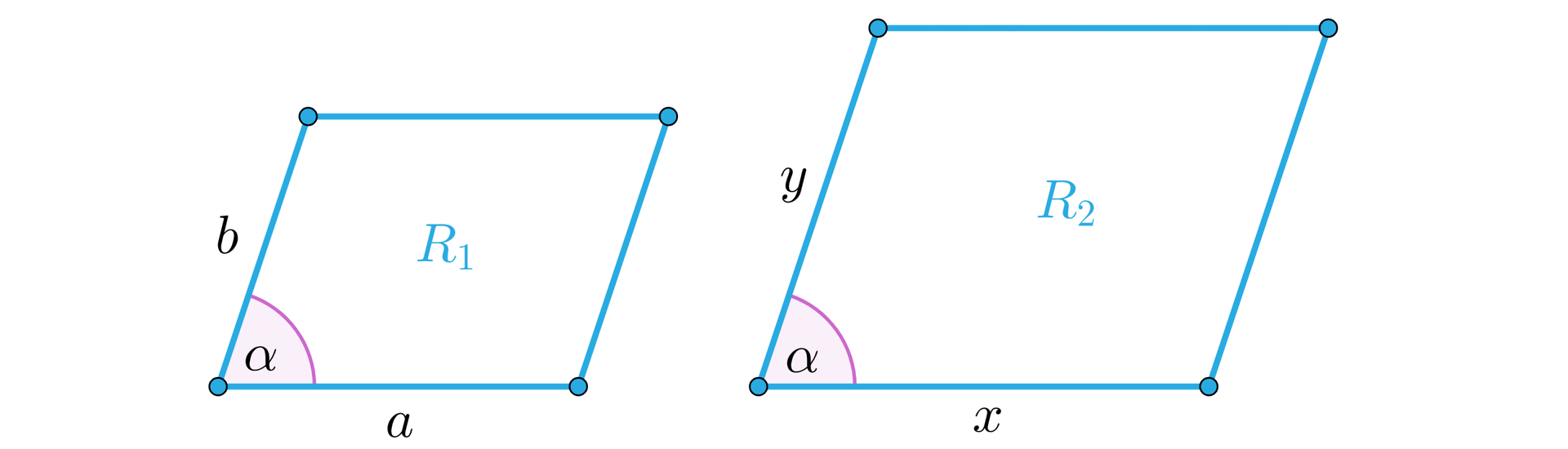
Niech $P_1$ będzie polem równoległoboku $R_1$. Zatem:

$P_1=a·b·\sin \alpha$

Niech $k$ ($k>0$) będzie skalą podobieństwa równoległoboku $R_2$ do równoległoboku $R_1$.

Wtedy $k^2=\frac{P}{P_1}$.

$k^2=\frac{P}{a·b·\sin \alpha }=\frac{P}{ab\sin \alpha }$, czyli $k=\sqrt{\frac{P}{ab\sin \alpha }}$

Wobec tego długości boków równoległoboku $R_2$ wynoszą:

$x=k·a=a·\sqrt{\frac{P}{ab\sin \alpha }}=\sqrt{\frac{aP}{b\sin \alpha }}$

$y=k·b=b·\sqrt{\frac{P}{ab\sin \alpha }}=\sqrt{\frac{bP}{a\sin \alpha }}$

Zatem obwód równoległoboku $R_2$ wynosi:

$L=2\cdot x+2\cdot y=2\cdot \left(\sqrt{\frac{aP}{b\sin \alpha }}+\sqrt{\frac{bP}{a\sin \alpha }}\right)$

figury, dla których istnieje podobieństwo, przekształcające jedną figurę na drugą