Infografika
Zapoznaj się z infografiką i odpowiedz na zamieszczone poniżej pytanie.
Wielkość ta pokrywa się także z tangensem kąta jaki tworzą sieczna z osią . Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y, bez zaznaczonych jednostek. W tym układzie zaznaczono wykres funkcji f, który zaczyna się w trzeciej ćwiartce układu współrzędnych otwartym punktem i rośnie prawie pionowo przecinając oś X do zamalowanego punktu znajdującego się w drugiej ćwiartce układu współrzędnych. Od tego punktu wykres funkcji f maleje do punktu znajdującego się w czwartej ćwiartce układu współrzędnych przecinając oś Y powyżej zera i oś X po stronie dodatnich argumentów. Od tego punktu rośnie do niezamalowanego punktu leżącego w pierwszej ćwiartce układu współrzędnych powyżej punktu leżącego w drugiej ćwiartce układu. Na wykresie leżącym w pierwszej ćwiartce zaznaczono pomarańczowy punkt o współrzędnych . Na wykresie leżącym w czwartej ćwiartce układu współrzędnych zaznaczono zielony punkt o współrzędnych . Odległość między tymi punktami oznaczono jako h, a różnicę wysokości między tymi punktami oznaczono . Prze zielony i pomarańczowy punkt poprowadzono sieczną g, która jest nachylona do osi X pod kątem alfa. Zapisano również wzór: . Punkt 2. Opis alternatywny
Przechodząc z punktami pośrednimi do punktu obserwujemy dążenie siecznych do stycznej do wykresu funkcji w punkcie . Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y, bez zaznaczonych jednostek. W tym układzie zaznaczono wykres funkcji f, który zaczyna się w trzeciej ćwiartce układu współrzędnych otwartym punktem i rośnie prawie pionowo przecinając oś X do zamalowanego punktu znajdującego się w drugiej ćwiartce układu współrzędnych. Od tego punktu wykres funkcji f maleje do punktu znajdującego się w czwartej ćwiartce układu współrzędnych przecinając oś Y powyżej zera i oś X po stronie dodatnich argumentów. Od tego punktu rośnie do niezamalowanego punktu leżącego w pierwszej ćwiartce układu współrzędnych powyżej punktu leżącego w drugiej ćwiartce układu. Na wykresie leżącym w czwartej ćwiartce układu współrzędnych zaznaczono zielony punkt. Przechodzi przez niego sieczna . Na wykresie leżącym w pierwszej ćwiartce zaznaczono dwa szare punkty i dwie sieczne przechodzące przez nie za pomocą przerywanych linii. Punkt 3. Opis alternatywny
Przechodząc z punktami pośrednimi do punktu ze strony lewej otrzymujemy taką samą styczną jak w punkcie 2. Oznacz to, że pochodna funkcji w punkcie istnieje oraz że jest ona równa współczynnikowi kierunkowemu stycznej . Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y, bez zaznaczonych jednostek. W tym układzie zaznaczono wykres funkcji f, który zaczyna się w trzeciej ćwiartce układu współrzędnych otwartym punktem i rośnie prawie pionowo przecinając oś X do zamalowanego punktu znajdującego się w drugiej ćwiartce układu współrzędnych. Od tego punktu wykres funkcji f maleje do punktu znajdującego się w czwartej ćwiartce układu współrzędnych przecinając oś Y powyżej zera i oś X po stronie dodatnich argumentów. Od tego punktu rośnie do niezamalowanego punktu leżącego w pierwszej ćwiartce układu współrzędnych powyżej punktu leżącego w drugiej ćwiartce układu. Na wykresie leżącym w czwartej ćwiartce układu współrzędnych zaznaczono zielony punkt. Przechodzi przez niego sieczna . Na wykresie leżącym w tej samej ćwiartce zaznaczono dwa szare punkty i dwie sieczne przechodzące przez nie za pomocą przerywanych linii. Obok znajduje się wzór . Punkt 4. Opis alternatywny
Przechodząc z punktami pośrednimi do punktu ze strony lewej otrzymujemy widoczną na grafice prostą. Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y, bez zaznaczonych jednostek. W tym układzie zaznaczono wykres funkcji f, który zaczyna się w trzeciej ćwiartce układu współrzędnych otwartym punktem i rośnie prawie pionowo przecinając oś X do zamalowanego punktu znajdującego się w drugiej ćwiartce układu współrzędnych. Od tego punktu wykres funkcji f maleje do punktu znajdującego się w czwartej ćwiartce układu współrzędnych przecinając oś Y powyżej zera i oś X po stronie dodatnich argumentów. Od tego punktu rośnie do niezamalowanego punktu leżącego w pierwszej ćwiartce układu współrzędnych powyżej punktu leżącego w drugiej ćwiartce układu. Na wykresie leżącym w drugiej ćwiartce układu współrzędnych zaznaczono zielony punkt. Przechodzi przez niego sieczna g. Na wykresie leżącym w tej samej ćwiartce zaznaczono dwa szare punkty i dwie sieczne przechodzące przez nie oraz zielony punkt za pomocą przerywanych linii. Punkt 5. Opis alternatywny
Przechodząc z punktami pośrednimi do punktu ze strony prawej otrzymujemy widoczną na grafice prostą. Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y, bez zaznaczonych jednostek. W tym układzie zaznaczono wykres funkcji f, który zaczyna się w trzeciej ćwiartce układu współrzędnych otwartym punktem i rośnie prawie pionowo przecinając oś X do zamalowanego punktu znajdującego się w drugiej ćwiartce układu współrzędnych. Od tego punktu wykres funkcji f maleje do punktu znajdującego się w czwartej ćwiartce układu współrzędnych przecinając oś Y powyżej zera i oś X po stronie dodatnich argumentów. Od tego punktu rośnie do niezamalowanego punktu leżącego w pierwszej ćwiartce układu współrzędnych powyżej punktu leżącego w drugiej ćwiartce układu. Na wykresie leżącym w drugiej ćwiartce układu współrzędnych zaznaczono zielony punkt. Przechodzi przez niego sieczna g. Na wykresie leżącym w drugiej i czwartej ćwiartce zaznaczono dwa szare punkty i dwie sieczne przechodzące przez nie oraz zielony punkt za pomocą przerywanych linii. Punkt 6. Opis alternatywny
Proste otrzymane w punktach 4 i 5 różnią się od siebie. Oznacza to, że funkcja nie posiada pochodnej w punkcie . Ilustracja przedstawia układ współrzędnych z poziomą osią X oraz pionową osią Y, bez zaznaczonych jednostek. W tym układzie zaznaczono wykres funkcji f, który zaczyna się w trzeciej ćwiartce układu współrzędnych otwartym punktem i rośnie prawie pionowo przecinając oś X do zamalowanego punktu znajdującego się w drugiej ćwiartce układu współrzędnych. Od tego punktu wykres funkcji f maleje do punktu znajdującego się w czwartej ćwiartce układu współrzędnych przecinając oś Y powyżej zera i oś X po stronie dodatnich argumentów. Od tego punktu rośnie do niezamalowanego punktu leżącego w pierwszej ćwiartce układu współrzędnych powyżej punktu leżącego w drugiej ćwiartce układu. Na wykresie leżącym w drugiej ćwiartce układu współrzędnych zaznaczono zielony punkt, w którym dochodzi do zmiany monotoniczności funkcji f. Przechodzą przez niego dwie sieczne prostopadłe do siebie.

1. {audio}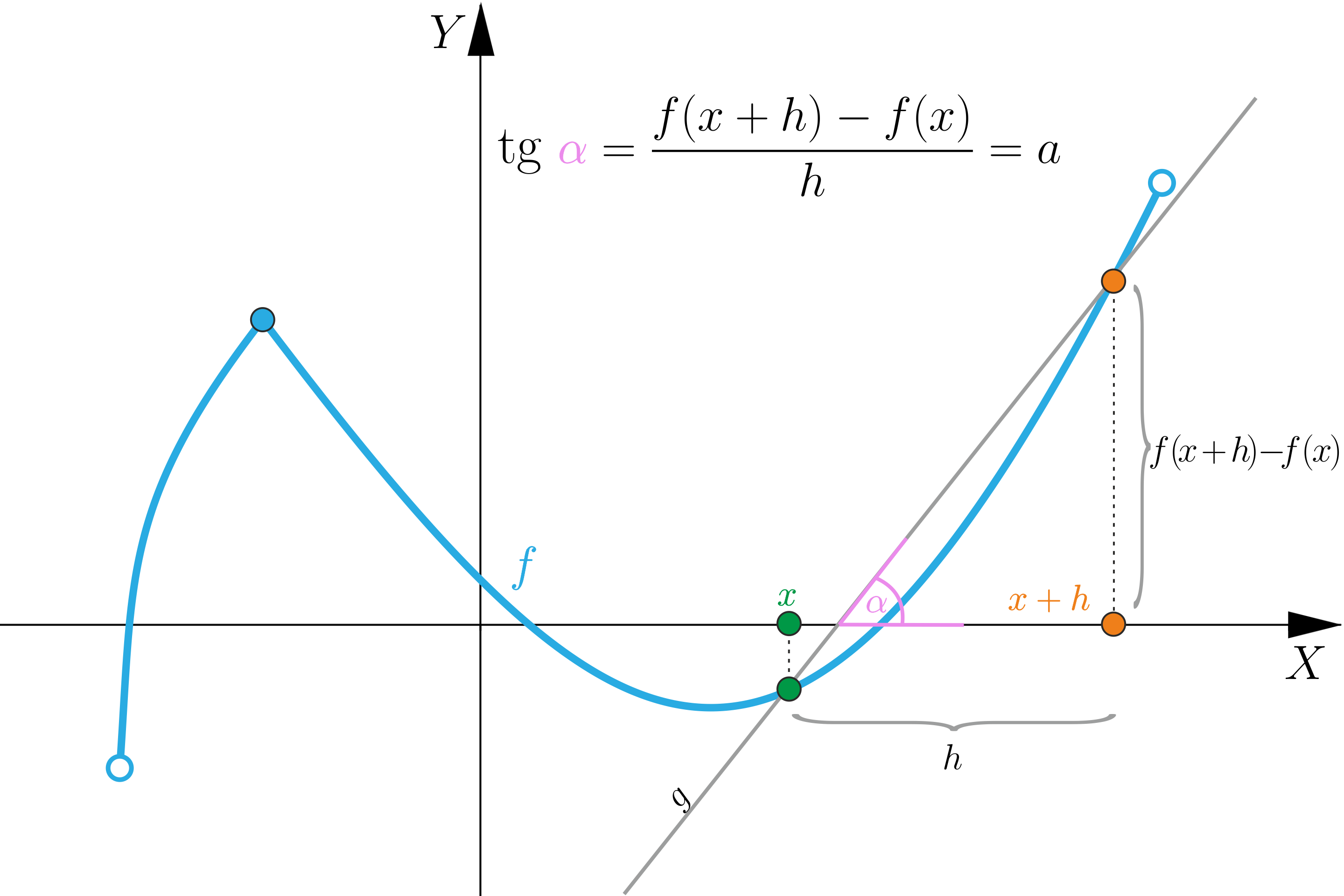
Współczynnik kierunkowy siecznej wykresu przechodzącej przez punkty oraz jest równy przestawionemu na grafice ilorazowi różnicowemu.
Wielkość ta pokrywa się także z tangensem kąta jaki tworzą sieczna z osią .
2. {audio}
Przechodząc z punktami pośrednimi do punktu obserwujemy dążenie siecznych do stycznej do wykresu funkcji w punkcie .
3. {audio}
Przechodząc z punktami pośrednimi do punktu ze strony lewej otrzymujemy taką samą styczną jak w punkcie 2. Oznacz to, że pochodna funkcji w punkcie istnieje oraz że jest ona równa współczynnikowi kierunkowemu stycznej .
4. {audio}
Przechodząc z punktami pośrednimi do punktu ze strony lewej otrzymujemy widoczną na grafice prostą.
5. {audio}
Przechodząc z punktami pośrednimi do punktu ze strony prawej otrzymujemy widoczną na grafice prostą.
6. {audio}
Proste otrzymane w punktach 4 i 5 różnią się od siebie. Oznacza to, że funkcja nie posiada pochodnej w punkcie .
Na podstawie zamieszczonego wykresu zaznacz te punkty spośród wyróżnionych, w których funkcja jest różniczkowalna.
