Infografika
Przeanalizuj infografikę, a następnie wykonaj polecenie .
Punkt przecięcia wykresów należy do zbioru rozwiązań każdego z równań – jest rozwiązaniem układu równań . Graficzna interpretacja układu równań wygląda następująco: na ilustracji znajduje się układ współrzędnych z poziomą osią x od minus trzech do czterech i pionową osią y od minus czterech do sześciu. Na płaszczyźnie narysowane zostały dwie proste opisane równaniami: pierwsza i druga . Proste przecinają się w jednym punkcie, który został zaznaczony zamalowaną kropką i podpisany literą A. Pod grafiką znajduje się napis: Jedno rozwiązanie postaci . Drugi rodzaj układu to układ nieoznaczony. Wykresy równań oraz pokrywają się.
Współrzędne każdego punktu leżącego na prostej są rozwiązaniem układu równań . Graficzna interpretacja układu równań wygląda następująco: na ilustracji znajduje się układ współrzędnych z poziomą osią x od minus trzech do czterech i pionową osią y od minus czterech do sześciu. Na płaszczyźnie narysowane zostały dwie proste opisane równaniami: pierwsza i druga . Proste pokrywają się. Pod grafiką znajduje się napis: Nieskończenie wiele rozwiązań postaci: . Trzeci rodzaj układu to układ sprzeczny. Wykresy równań oraz nie mają punktów wspólnych.
Układ równań nie posiada rozwiązania. >. Graficzna interpretacja układu równań wygląda następująco: na ilustracji znajduje się układ współrzędnych z poziomą osią x od minus trzech do czterech i pionową osią y od minus czterech do sześciu. Na płaszczyźnie narysowane zostały dwie proste opisane równaniami: pierwsza i druga . Proste są do siebie równoległe i nie przecinają się w żadnym punkcie. Pod grafiką znajduje się napis: Brak rozwiązań.

1. {audio}Niewiadome i .
2. {audio}Niewiadome i .
3. {audio}Współczynniki przy niewiadomej .
4. {audio}Współczynnik przy niewiadomej .
5. {audio}Współczynnik przy niewiadomej .
6. {audio}Wyrazy wolne.
7. {audio}Wykresy równań oraz przecinają się w jednym punkcie.
Punkt przecięcia wykresów należy do zbioru rozwiązań każdego z równań – jest rozwiązaniem układu równań .
8. {audio}Wykresy równań oraz pokrywają się.
Współrzędne każdego punktu leżącego na prostej są rozwiązaniem układu równań .
9. {audio}Wykresy równań oraz nie mają punktów wspólnych.
Układ równań nie posiada rozwiązania.
Rysunek przedstawia interpretacje geometryczne trzech różnych układów równań.
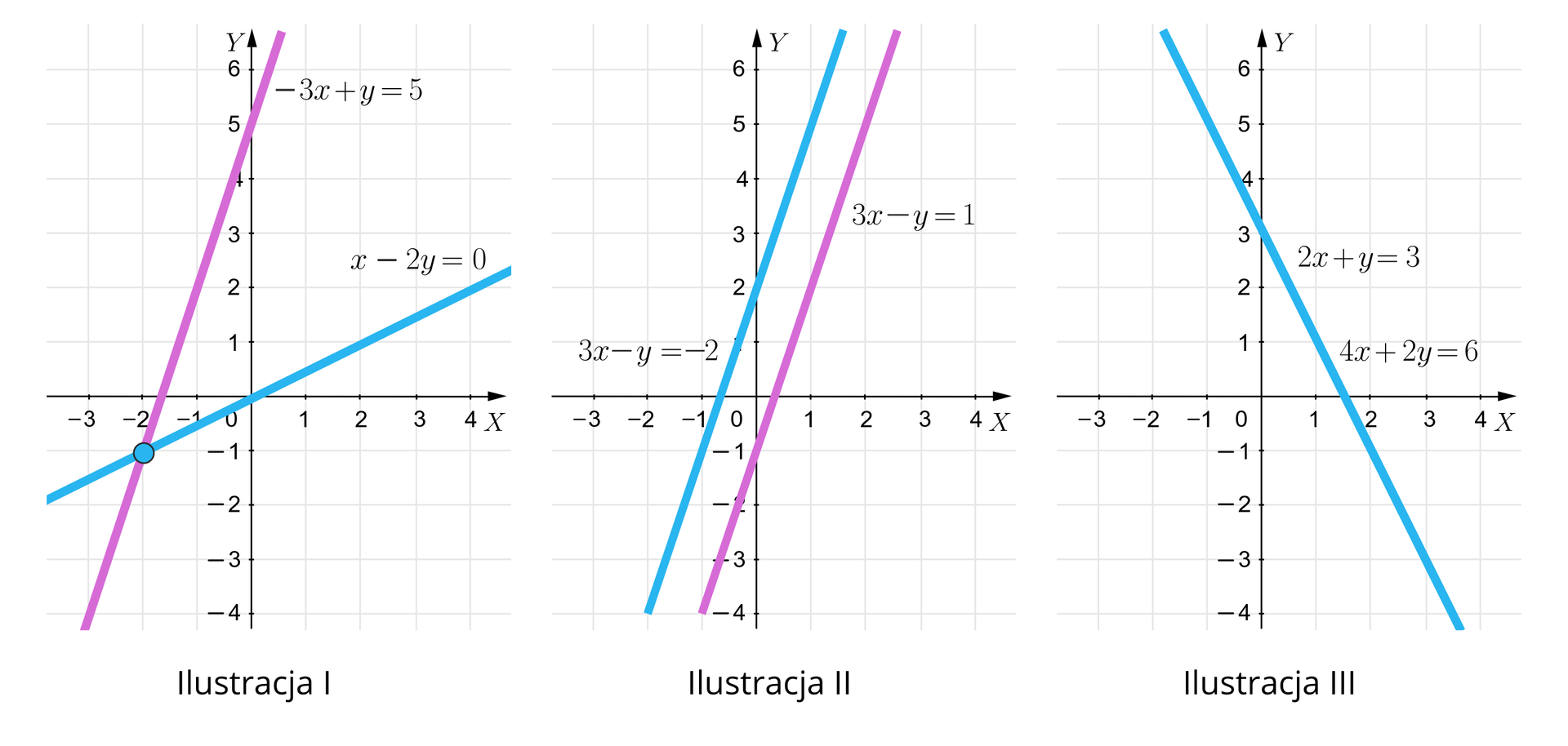
Dopasuj przeciągając poprawne rozwiązania oraz nazwy do interpretacji geometrycznych danych układów równań.
układ nieoznaczony, nieskończenie wiele rozwiązań
- pary postaci , układ oznaczony, układ sprzeczny, , brak rozwiązań
Ilustracja I
Nazwa: ............................................................................................................, rozwiązanie: .............................................................................................................
Ilustracja II
Nazwa: ............................................................................................................, rozwiązanie: .............................................................................................................
Ilustracja III
Nazwa: ............................................................................................................, rozwiązanie: .............................................................................................................
Druga ilustracja przedstawia układ współrzędnych z poziomą osią x od minus trzech do czterech i pionową osią y od minus czterech do sześciu. Na płaszczyźnie znajdują się dwie proste o równaniach oraz . Proste są do siebie równoległe. Opisana ilustracja przedstawia 1. układ sprzeczny, 2. układ nieoznaczony, 3. nieskończenie wiele rozwiązań- pary postaci , 4. , 5. brak rozwiązań, 6. układ oznaczony, którego rozwiązanie to 1. układ sprzeczny, 2. układ nieoznaczony, 3. nieskończenie wiele rozwiązań- pary postaci , 4. , 5. brak rozwiązań, 6. układ oznaczony.
Trzecia ilustracja przedstawia układ współrzędnych z poziomą osią x od minus trzech do czterech i pionową osią y od minus czterech do sześciu. Na płaszczyźnie znajdują się dwie proste o równaniach oraz . Proste nakładają się na siebie. Opisana ilustracja przedstawia 1. układ sprzeczny, 2. układ nieoznaczony, 3. nieskończenie wiele rozwiązań- pary postaci , 4. , 5. brak rozwiązań, 6. układ oznaczony, którego rozwiązanie to 1. układ sprzeczny, 2. układ nieoznaczony, 3. nieskończenie wiele rozwiązań- pary postaci , 4. , 5. brak rozwiązań, 6. układ oznaczony.