Kula i sfera
Elementy kuli
Krople rosy, bryłki gradu, ziarenka maku swoim kształtem przypominają kule.

Jaka bryła powstanie w wyniku obrotu półkola wokół prostej, na której leży średnica tego półkola?

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1F7mMmuS
Kulę można otrzymać w wyniku obrotu półkola wokół prostej, na której leży jego średnica lub w wyniku obrotu koła wokół prostej przechodzącej przez jego środek.
Promień tego koła to promień kuli, a środek koła – środek kuli.
Kulę w przestrzeni definiujemy podobnie jak koło na płaszczyźnie.
Kula to zbiór wszystkich punktów przestrzeni, których odległość od punktu, zwanego środkiem, jest nie większa od długości odcinka, zwanego promieniem kuli.

W przestrzeni odpowiednikiem okręgu jest sfera.
Sfera to zbiór wszystkich punktów przestrzeni, których odległość od punktu, zwanego środkiem, jest równa długości odcinka, zwanego promieniem sfery.

Film dostępny pod adresem https://zpe.gov.pl/a/D1F7mMmuS
Animacja
Film dostępny pod adresem https://zpe.gov.pl/a/D1F7mMmuS
Animacja
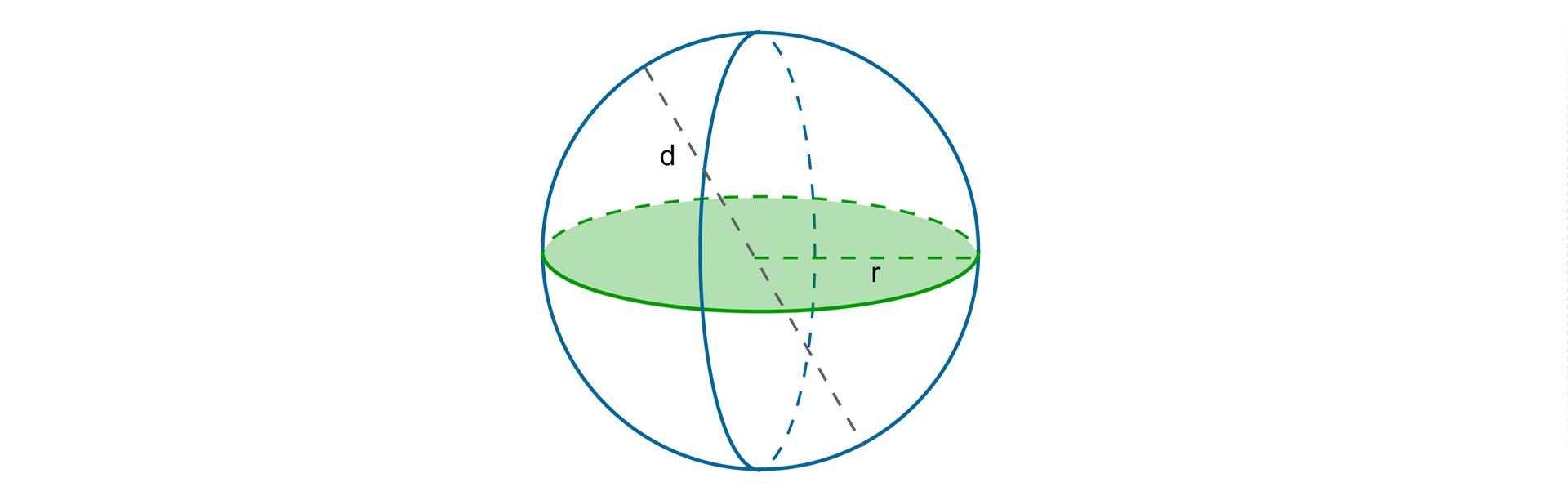
Cięciwa sfery (kuli) to odcinek o końcach leżących na sferze. Cięciwa przechodząca przez środek sfery (kuli), to średnica

Promień kuli jest równy .
Określ długość średnicy kuli.
Określ największą odległość dwóch punktów leżących na sferze tej kuli.
Czy cięciwa tej kuli może mieć długość , , ?
Przekroje kuli
Przetnij pomarańczę na dwie części. Jakie kształty mają tak otrzymane przekroje?

Przekrojem kuli jest koło (lub punkt). Jeśli płaszczyzna przecinająca kulę przechodzi przez jej środek, to otrzymany przekrój nazywamy kołem wielkim kuli. Płaszczyzna ta dzieli kule na dwie półkule.

Pole koła wielkiego kuli jest równe . Oblicz średnicę tej kuli.
Obliczamy promień koła wielkiego kuli.
bo
Średnica kuli jest równa średnicy koła wielkiego.
Średnica kuli jest równa .
Promień kuli jest równy . W odległości od płaszczyzny koła wielkiego tej kuli poprowadzono przekrój. Oblicz obwód tego przekroju.
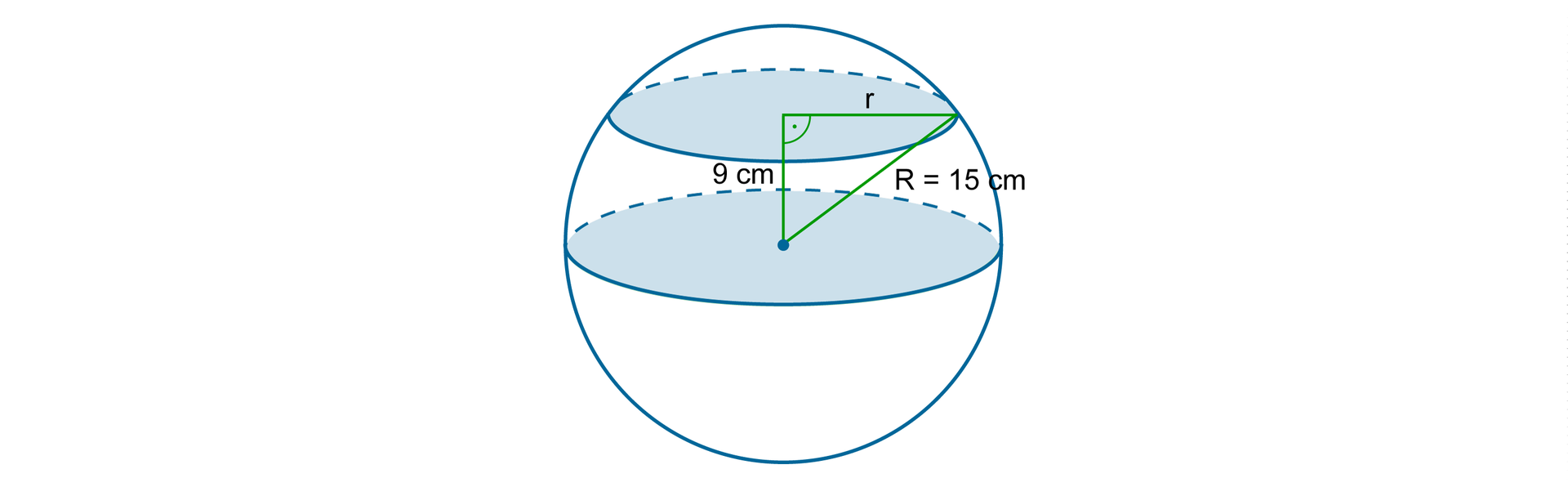
Aby obliczyć obwód przekroju, obliczymy najpierw jego promień r.
Zauważmy, że trójkąt utworzony przez promień kuli, promień przekroju i odcinek łączący przekroje kuli i prostopadły do nich, jest prostokątny.
Korzystamy z twierdzenia Pitagorasa.
Obliczamy teraz obwód przekroju.
Obwód przekroju jest równy .
Pole powierzchni kuli

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1F7mMmuS
Obierz pomarańczę. Czy możesz tak otrzymane skórki rozłożyć płasko na stole?
Archimedes (ok. p.n.e.) był greckim filozofem, przyrodnikiem i matematykiem. Odkrył prawo wyporu, zwane dzisiaj prawem Archimedesa. Wynalazł między innymi organy wodne, wielokrążek, przenośnik śrubowy (urządzenie do przemieszczania materiałów sypkich lub cieczy).
Wyprowadził wzór na obliczenie pola powierzchni kuli, wykorzystując nowatorskie pomysły, które obecnie wchodzą w zakres rachunku różniczkowego i całkowego.
Archimedes wykazał, że pole powierzchni kuli jest czterokrotnie większe od pola jej koła wielkiego.
Pole powierzchni kuli
Pole powierzchni kuli o promieniu jest równe
Film dostępny pod adresem https://zpe.gov.pl/a/D1F7mMmuS
Animacja
Na toczek w kształcie półkuli zużyto filcu. Jaki obwód ma głowa osoby, dla której go wykonano?
Obliczymy promień półkuli, w kształcie której jest toczek.
Obliczamy obwód głowy osoby, dla której wykonano toczek.
Obwód głowy osoby, dla której wykonano toczek, jest równy około .
Objętość kuli

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1F7mMmuS
Film dostępny pod adresem https://zpe.gov.pl/a/D1F7mMmuS
Animacja
Objętość kuli
Objętość kuli o promieniu jest równa
Objętość kuli można obliczyć zgodnie z zasadą siedemnastowiecznego matematyka włoskiego Bonaventury Cavalieriego.
Na podstawie rozważań Cavaleriego można wywnioskować, że objętość półkuli o promieniu jest równa różnicy objętości walca o promieniu podstawy oraz wysokości i objętości stożka o promieniu podstawy i wysokości .

Kula z ciasta ma promień . Ile ciasteczek w kształcie kulek o promieniu każde można otrzymać z tego ciasta?
Obliczamy najpierw objętość dużej kuli ciasta.
Teraz obliczamy objętość ciasteczka.
Obliczamy, ile ciasteczek można otrzymać z dużej kuli ciasta.
Z ciasta można otrzymać ciasteczek.
Objętość kuli jest równa . Oblicz pole powierzchni tej kuli.
Obliczamy najpierw promień R kuli.
Możemy już obliczyć pole powierzchni kuli.
Pole powierzchni kuli jest równe .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1F7mMmuS
Uzupełnij, wpisując odpowiednie liczby.
Pole powierzchni kuli | |||
o promieniu jest równe | o średnicy jest równe | O promieniu jest równe | O średnicy jest równe |
Promień kuli jest równy .
Pole koła wielkiego tej kuli jest równe …
Pole powierzchni kuli jest równe …
Objętość kuli jest równa …
Igloo ma kształt półkuli, której promień zewnętrzny jest równy .
Pole powierzchni zewnętrznej igloo jest równe

Średnica tej piłeczki jest równa: Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Objętość jednej piłeczki do tenisa ziemnego wynosi .
Średnica tej piłeczki jest równa:
Średnice wewnętrzne dwóch doniczek wynoszą odpowiednio: i . W której doniczce mieści się więcej ziemi i o ile ?
Pole powierzchni nadmuchanego balona jest równe . Ile powietrza mieści się w tym balonie? Przyjmij . Wynik podaj z dokładnością do .
Do pustego akwarium w kształcie półkuli wlano wody.
Akwarium wypełnione jest teraz w wodą. Ile szkła użyto na jego wykonanie?
Zapisz, jak zmieni się objętość kuli, gdy jej promień
zwiększono dwukrotnie
zwiększono pięciokrotnie
zmniejszono dwukrotnie
zmniejszono trzykrotnie
Oblicz pole powierzchni i objętość kuli, gdy
średnica kuli jest równa
pole koła wielkiego jest równe
Świeczkę w kształcie walca przetopiono na świeczkę w kształcie kuli. Oblicz promień tej kuli.
Wynik podaj z dokładnością do .

Promień kuli jest równy . W jakiej odległości od płaszczyzny koła wielkiego tej kuli poprowadzono jej przekrój, jeśli obwód tego przekroju wynosi ?
Pole powierzchni całkowitej półkuli wynosi . Oblicz objętość i pole powierzchni całej kuli.
Kulę o średnicy przecięto na dwie jednakowe części. Jakie pole powierzchni ma każda z otrzymanych półkuli ?
Z kuli o promieniu odcięto czaszę w odległości od środka kuli. Oblicz stosunek pola powierzchni otrzymanego przekroju do pola koła wielkiego.
Przekrój osiowy kuli ma pole powierzchni równe . Oblicz pole powierzchni i objętość tej kuli.
Jakie pole powierzchni ma ta kula? Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Obwód koła wielkiego kuli jest równy .
Jakie pole powierzchni ma ta kula?
Koło o obwodzie obraca się wokół swojej średnicy. Jakie pole ma koło wielkie otrzymanej kuli?
Jaką figurę otrzymamy, obracając okrąg wokół jego średnicy?
Do pojemnika w kształcie sześcianu o krawędzi włożono kulkę o średnicy . Jaką część pojemności sześcianu zajmuje kula ?
Do menzurki w kształcie walca o średnicy podstawy równej wrzucono metalową kulkę o promieniu . Ile wody należy wlać do tej menzurki, aby kulka była zakryta?
Niech będzie objętością kuli o promieniu , a objętością stożka o promieniu podstawy oraz wysokości też . Oblicz stosunek .
Kula i stożek mają jednakowe objętości. Kula ma promień długości . Promień podstawy stożka ma długość . Oblicz wysokość stożka?
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Przekrój kuli może być punktem.
- Każdy przekrój kuli jest okręgiem.
- Objętość kuli jest proporcjonalna do sześcianu promienia kuli.