Walec i stożek mają taki sam promień podstawy i taką samą wysokość.
Zaobserwuj, jak zmienia się stosunek objętości stożka do objętości walca wraz ze zmianą wysokości brył.

R4XyhkTxvNIxb1

Animacja przedstawia walec i stożek o tym samym promieniu podstawy i tej samej wysokości. Objętość walca równa się 30,3 a objętość stożka równa się 10,1. Iloraz objętości walca do objętości stożka (V walca do V stożka) = 30,3 dzielone przez 10,1 =3.

Animacja przedstawia walec i stożek o tym samym promieniu podstawy i tej samej wysokości. Objętość walca równa się 30,3 a objętość stożka równa się 10,1. Iloraz objętości walca do objętości stożka (V walca do V stożka) = 30,3 dzielone przez 10,1 =3.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DBpgxRP4R

Oblicz objętość stożka, którego wysokość jest równa $36\mathrm{ cm}$, a promień podstawy $4\mathrm{ cm}$.
Do wzoru na objętość stożka

podstawiamy:

Objętość stożka jest równa $192\mathrm{\pi }{\mathrm{cm}}^2$.

Ile porcji lodów można otrzymać z $1\mathrm{ l}$ masy lodowej?

RDBKBtbypvd7Y1

Rysunek dwóch trójkątów sklejonych podstawami o długości 6 cm. Wysokość pierwszego trójkąta wynosi 8 cm a drugiego trójkąta wynosi 10 cm.

Obliczymy objętość masy lodowej potrzebnej do wykonania jednej porcji lodów, czyli objętość dwóch stożków o wspólnej podstawie. Wysokość jednego z  tych stożków jest równa $10\mathrm{ cm}$, a drugiego $8\mathrm{ cm}$. Promień podstawy każdego ze stożków jest równy $6\mathrm{ cm}: 2= 3\mathrm{ cm}$.

Na wykonanie jednej porcji lodów potrzeba około $\mathrm{169,56} {\mathrm{cm}}^3$ masy lodowej.
Obliczamy teraz, ile lodów można otrzymać z $1\mathrm{ l}$ masy lodowej.
Ponieważ $1\mathrm{ l }=1000\mathrm{ ml}$, a $1\mathrm{ ml }= 1 {\mathrm{cm}}^3$, zatem $1\mathrm{l }= 1000 {\mathrm{cm}}^3$.

Z $1\mathrm{ l}$ masy lodowej można wykonać $5$ lodów.

Świeca wykonana z wosku o gęstości $\mathrm{0,9}g/{\mathrm{cm}}^3$ ma masę $\mathrm{0,231}\mathrm{ kg}$. Świeca ma kształt stożka o średnicy podstawy równej $70\mathrm{ mm}$. W czasie godziny wysokość palącej się świecy zmniejsza się przeciętnie o 1 cm. Świecę zapalono o godzinie $20.00$. O której godzinie zgaśnie ta świeca?
Przyjmij $\pi =\frac{22}{7}$.
Gęstość wosku podana jest w $g/{\mathrm{cm}}^3$. Średnicę świecy zapiszemy więc w centymetrach, a jej masę w gramach, aby ujednolicić jednostki.

R1DYp7AYxNZCE1

Rysunek stożka o wysokości H i średnicy podstawy 70 mm.

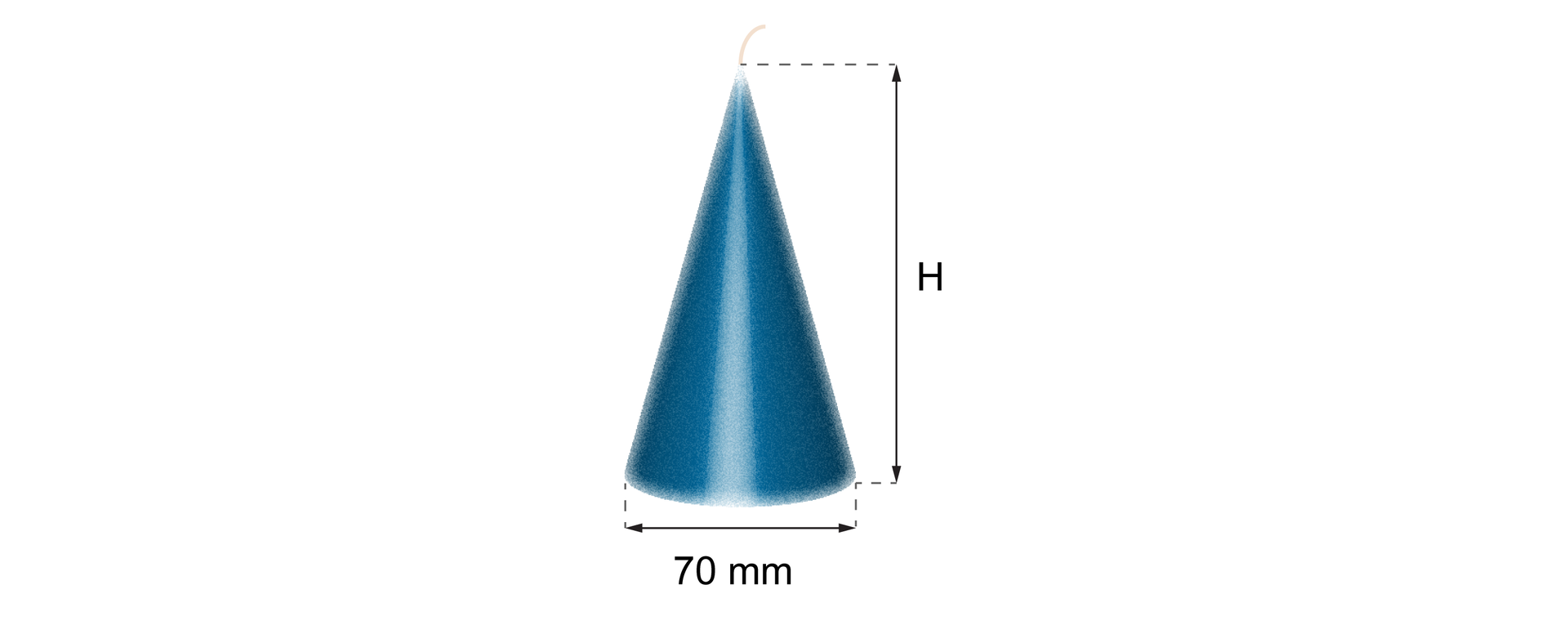
Oznaczmy:
$H$ – wysokość świecy.
Objętość $V$ stożka, w kształcie którego jest świeca, jest równa

Stąd

Zapisujemy równość wynikającą z tego, że masa substancji to iloczyn zajmowanej przez nią objętości przez gęstość tej substancji.

Z  zapisanej równości wyznaczamy wysokość świecy.

W czasie godziny wysokość świecy zmniejsza się o $1\mathrm{ cm}$, czyli świeca będzie paliła się $20$ godzin.
Świecę zapalono o godzinie $20.00$, do północy paliła się więc $4$ godziny i $16$ godzin po północy.
Świeca zgaśnie o godzinie $16.00$ następnego dnia.

Przekrojem osiowym stożka jest trójkąt, którego tworząca jest równa $12\mathrm{ dm}$. Pole powierzchni bocznej stożka jest równe $48\pi \sqrt{5}{\mathrm{ dm}}^2$. Oblicz objętość stożka.

RWOwoAXPr294M1

Rysunek stożka o wysokości H, promieniu podstawy r i tworzącej równej 12. Zaznaczony trójkąt będący przekrojem osiowym stożka.

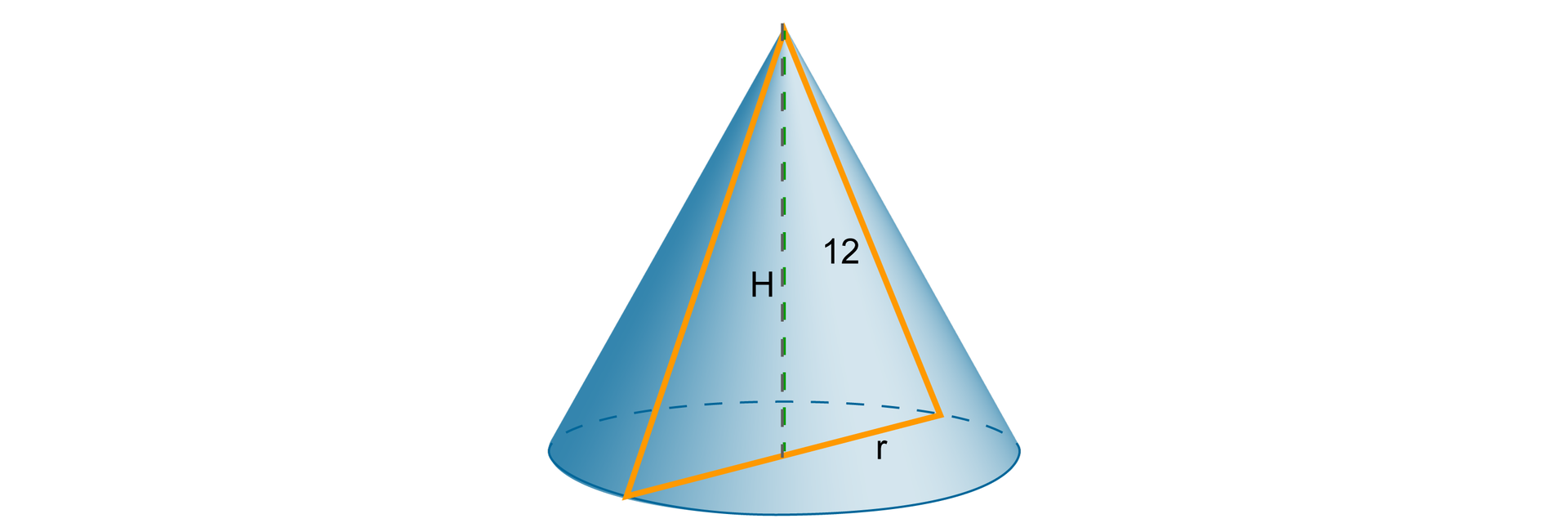
Aby obliczyć objętość stożka, należy najpierw znaleźć wysokość stożka i  promień jego podstawy.
Promień $r$ podstawy stożka znajdujemy, korzystając z tego, że pole powierzchni bocznej stożka jest równe $48\pi \sqrt{5}{\mathrm{ dm}}^2$.

Zauważmy, że wysokość stożka jest zarazem wysokością jego przekroju osiowego. Zatem trójkąt, którego boki mają długości $H,r,12$ (jak na rysunku), jest prostokątny.
Zapisujemy dla tego trójkąta równość wynikającą z twierdzenia Pitagorasa i wyznaczamy wysokość stożka.

Obliczamy objętość stożka.

Objętość stożka jest równa $213\frac{1}{3}\cdot \mathrm{\pi }{\mathrm{cm}}^3$.

Element ma kształt walca, na którym umieszczony jest stożek.
Przekrojem osiowym tego walca jest kwadrat o polu $9 m^2$. Objętość całej bryły wynosi $\mathrm{25,905} m^2$. Oblicz, ile puszek farby należy zakupić, aby pomalować cały element, jeżeli zawartość jednej puszki wystarcza na pomalowanie $5m^2$ powierzchni. Przyjmij $\pi =\mathrm{3,14}$.
Oznaczmy

• $r$ - promień podstawy walca,

• $H$ - wysokość walca,

• $h$ – wysokość stożka,

• $l$- długość tworzącej stożka.

  REIBCKaHrTqcx1

  Rysunek walca i umieszczonego na nim stożka o promieniach podstaw długości r. Wysokość walca równa jest H, wysokość stożka długości h oraz tworząca stożka równa l.

  

  Przekrojem osiowym walca jest kwadrat o polu $9 m^2$. Wynika z tego, że długość boku tego kwadratu jest równa $\sqrt{9}\mathrm{ cm}$, czyli $3\mathrm{ cm}$. Wysokość walca $H$ jest więc równa $3\mathrm{ m}$, a promień jego podstawy $\mathrm{r }= 3\mathrm{ m }: 2 = \mathrm{1,5}\mathrm{ m}$. Objętość elementu jest równa sumie objętości walca i stożka.

  $\pi r^2\cdot H+\frac{1}{3}\pi r^2\cdot h=\mathrm{25,905}$

  Dla ułatwienia obliczeń wyłączamy z obu składników wspólne czynniki poza nawias.

  $\pi r^2\left(H+\frac{1}{3}h\right)=\mathrm{25,905}$
  $\mathrm{3,14}\cdot {\left(\mathrm{1,5}\right)}^2\cdot \left(3+\frac{1}{3}h\right)=\mathrm{25,905}$
  $\mathrm{7,065}\left(3+\frac{1}{3}h\right)=\mathrm{25,905}/ : \mathrm{3,14}$
  $\mathrm{2,25}\left(\frac{9+h}{3}\right)=\mathrm{8,25}$
  $\mathrm{0,75}\left(9+h\right)=\mathrm{8,25}/: \mathrm{0,75}$
  $9+h=11$
  $h=2\mathrm{ m}$

  Teraz , korzystając z twierdzenia Pitagorasa, obliczamy długość tworzącej stożka.

  $l^2=h^2+r^2$
  $l=\sqrt{2^2+{\left(\mathrm{1,5}\right)}^2}=\sqrt{\mathrm{6,25}}=\mathrm{2,5}$
  $l=\mathrm{2,5}\mathrm{ cm}$

  Obliczamy pole $P$ powierzchni całkowitej elementu, czyli sumę pola koła (podstawy bryły), pola powierzchni bocznej walca i pola powierzchni bocznej stożka.

  $P=\pi r^2+2\mathrm{\pi r}\cdot H+\mathrm{\pi rl}$
  $P=\mathrm{\pi r}\left(r+2H+l\right)$
  $P=\mathrm{3,14}\cdot \mathrm{1,5}\left(\mathrm{1,5}+2\cdot 3+\mathrm{2,5}\right)$
  $P=\mathrm{4,71}\cdot 10=\mathrm{47,1}$
  $P=\mathrm{47,1} m^2$

  Jedna puszka farby wystarcza na pomalowanie $5 m^2$ powierzchni. Ponieważ $\mathrm{47,1}:5=\mathrm{9,42}$ , zatem należy kupić $10$ puszek farby.