Stożek. Pole powierzchni stożka
Zaobserwuj, jaką bryłę otrzymujemy w wyniku obrotu trójkąta prostokątnego wokół jednej z przyprostokątnych. W kształcie jakiej figury jest podstawa bryły? Ile ma wierzchołków?

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DbKCVKgzF
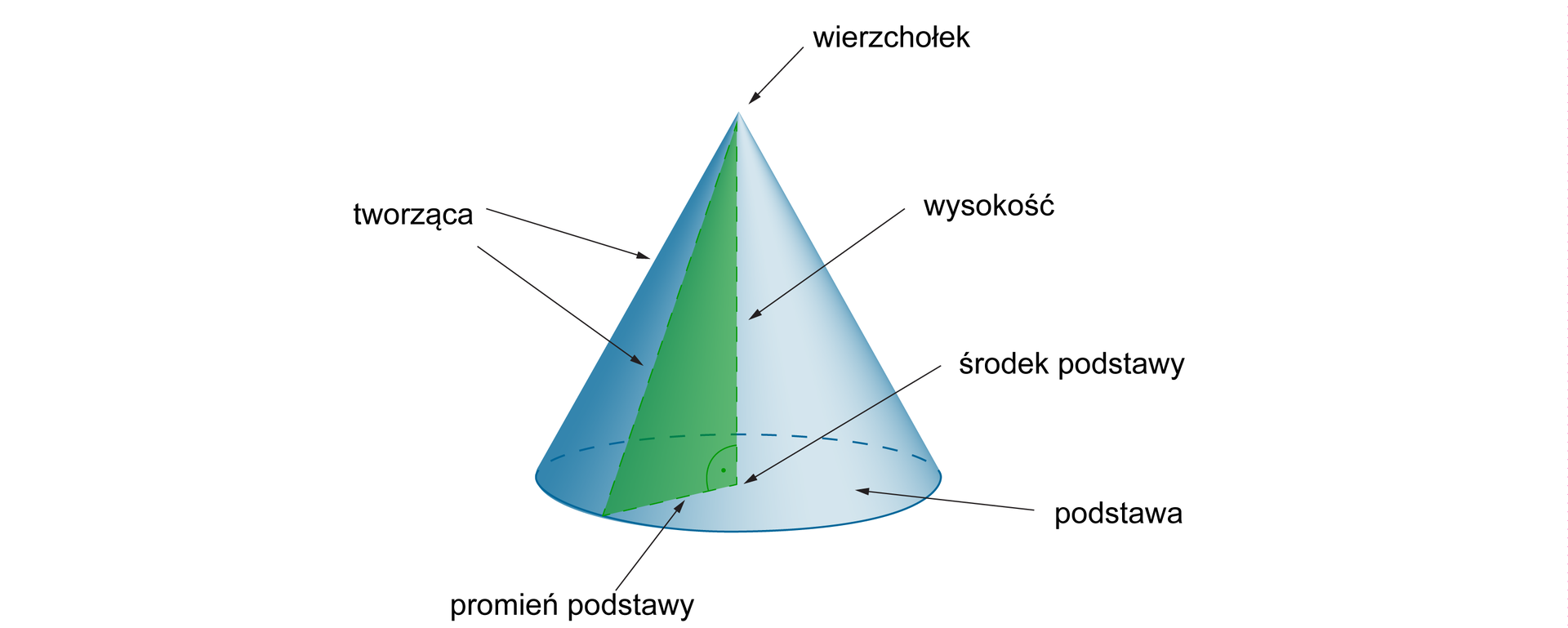
W wyniku obrotu trójkąta prostokątnego wokół prostej, na której leży jedna z przyprostokątnych, otrzymujemy bryłę, zwaną stożkiem.
Prosta ta jest osią obrotu stożka. Jest to również oś symetrii stożka. Podstawą stożka jest koło. Wysokość stożka jest równa przyprostokątnej, wokół której obracaliśmy trójkąt, a promień r podstawy jest równy drugiej z przyprostokątnych. Wysokość jest prostopadła do płaszczyzny, na której leży podstawa stożka, a więc i do każdego z promieni podstawy.
Wierzchołek obracanego trójkąta nieleżący na podstawie to wierzchołek stożka.
Przeciwprostokątna obracanego trójkąta zakreśliła powierzchnię boczną stożka. Jest ona tworzącą stożka. Tworzącą stożka jest zatem każdy odcinek łączący wierzchołek stożka z punktem leżącym na okręgu będącym brzegiem podstawy.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DbKCVKgzF
Na oklejenie kartonowej czapeczki w kształcie stożka zużyto niebieskiej taśmy.
Wysokość czapeczki jest trzykrotnie większa od promienia podstawy. Oblicz tę wysokość. Przyjmij
Z treści zadania wynika, że długość okręgu, będącego brzegiem podstawy stożka, w kształcie którego jest czapeczka, jest równy .
Obliczmy promień r tego okręgu.
Wysokość czapeczki jest trzykrotnie większa od promienia, czyli wynosi
W trójkącie równoramiennym kąt między ramionami ma miarę , a ramię ma długość .
Trójkąt ten obrócono wokół prostej, na której leży wysokość . Oblicz średnicę podstawy tak utworzonego stożka i jego wysokość.

Kąt jest połową kąta , ma zatem miarę .
Trójkąt jest więc trójkątem prostokątnym, w którym jeden z kątów ostrych ma miarę . Z własności takiego trójkąta wynika, że
Zatem wysokość stożka jest równa , a średnica podstawy ma długość
Przekroje stożka
Przyjrzyj się przekrojom stożka. Jaki kształt ma przekrój osiowy? Jaki kształt ma przekrój poprzeczny?
Dowiedz się, jak nazywa się figura otrzymana w wyniku przekroju stożka płaszczyzną, która nie jest ani równoległa, ani prostopadła do podstawy.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DbKCVKgzF
Przekrój osiowy stożka jest trójkątem równoramiennym. Podstawa tego trójkąta jest równa średnicy podstawy stożka, ramię jest równe tworzącej, a wysokość poprowadzona z wierzchołka między ramionami jest równa wysokości stożka.

Przekrój poprzeczny stożka jest kołem. Promień tego koła jest nie większy od promienia podstawy stożka.

Przekrój osiowy stożka jest trójkątem, w którym jeden z kątów ma miarę . Znajdź miary pozostałych kątów tego trójkąta.
Trójkąt będący przekrojem osiowym stożka jest równoramienny. Kąt o mierze jest kątem rozwartym, zatem jest kątem między ramionami tego trójkąta. Kąty przy podstawie trójkąta równoramiennego mają równe miary.
Każdy z nich jest więc równy
Pozostałe kąty trójkąta są równe , .
Wysokość stożka jest równa , a średnica podstawy ma długość . W odległości od wierzchołka przecięto stożek płaszczyzną prostopadłą do wysokości. Oblicz pole tak utworzonego przekroju.

Oznaczmy:
- wierzchołek stożka,
- środek przekroju poprzecznego,
- promień przekroju poprzecznego,
- promień podstawy stożka,
- wysokość stożka.
Zauważmy, że trójkąty i są podobne na podstawie cechy podobieństwa trójkątów kąt‑kąt‑kąt. Istotnie: oba trójkąty są prostokątne, kąt jest kątem wspólnym obu trójkątów i - jako kąty odpowiadające przy prostych równoległych.
Zapisujemy proporcję wynikającą z podobieństwa tych trójkątów i wyznaczamy promień przekroju poprzecznego.
Obliczamy pole przekroju.
Pole przekroju stożka jest równe .
Siatka stożka
Wytnij z papieru trzy koła.
Pierwsze koło przetnij na pół. Drugie przetnij wzdłuż średnic na 4 równe części. Z trzeciego wytnij dowolny wycinek koła. Zwiń wycięte figury tak, aby otrzymać „czapeczkę”.
Jaki ma kształt każda z otrzymanych „czapeczek”?

Film dostępny pod adresem https://zpe.gov.pl/a/DbKCVKgzF
Aniamcja
Wytnij z papieru koło. Oznacz jego środek , a promień . Przetnij koło wzdłuż promienia i zwiń tak, aby promienie wyznaczone przez miejsce przecięcia pokryły się. Zepnij tak otrzymaną powierzchnię boczną stożka.
Jaka jest długość tworzącej ?
Jak obliczyć promień podstawy?
Który z punktów koła jest wierzchołkiem stożka?
W jakim kształcie jest powierzchnia boczna stożka?
Z jakich figur składa się powierzchnia całkowita stożka?
Zaobserwuj, jak zmienia się powierzchnia boczna stożka, gdy zmieniamy jego wysokość.
Jaka jest długość promienia podstawy stożka, a jaka tworzącej, gdy powierzchnia boczna jest półkolem?

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DbKCVKgzF
Powierzchnia boczna stożka, po rozłożeniu na płaszczyźnie, jest wycinkiem kołowym.
Siatka stożka składa się z koła, będącego podstawą stożka i wycinka koła, będącego powierzchnią boczną.
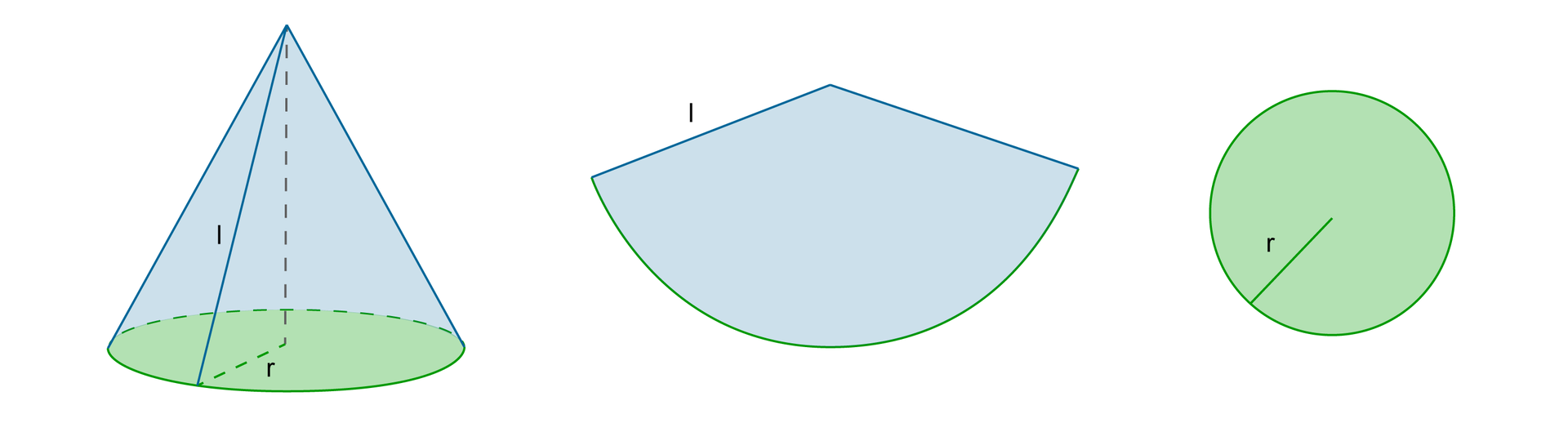
Tworząca stożka jest równa promieniowi wycinka koła, będącego powierzchnią boczną stożka .
Obwód podstawy stożka jest równy długości łuku wyznaczonego przez wycinek koła, będący powierzchnią boczną.

Powierzchnia boczna stożka po rozwinięciu na płaszczyźnie jest półkolem, którego promień jest równy . Oblicz wysokość stożka.
Obliczamy najpierw promień podstawy stożka.
Aby obliczyć wysokość stożka, korzystamy z twierdzenia Pitagorasa dla trójkąta, którego boki mają długości .

Wysokość stożka jest równa .
Podstawą stożka jest koło o promieniu . Powierzchnia boczna po rozwinięciu na płaszczyźnie jest wycinkiem koła o promieniu . Oblicz miarę kąta środkowego wyznaczającego ten wycinek.
Obliczamy obwód podstawy stożka.
Oznaczmy: - miara kąta środkowego wyznaczającego wycinek, będący powierzchnią boczną stożka.
Obliczamy długość łuku wyznaczającego wycinek koła.
Porównujemy obwód podstawy stożka i długość łuku wycinka koła i wyznaczamy .
Miara kąta środkowego wyznaczającego wycinek koła, będący powierzchnią boczną stożka, jest równa .
Pole powierzchni stożka
Oblicz pole powierzchni bocznej stożka, która po rozwinięciu na płaszczyźnie jest wycinkiem koła o promieniu . Promień podstawy tego stożka jest równy .
Pole powierzchni bocznej obliczymy jako pole wycinka koła. Niech będzie kątem środkowym tego wycinka. Wtedy
Zapisujemy i przekształcamy równość wynikającą z tego, że długość łuku okręgu wyznaczonego przez wycinek jest równa obwodowi podstawy stożka.
Stąd
Pole powierzchni bocznej jest równe .

Film dostępny pod adresem https://zpe.gov.pl/a/DbKCVKgzF
Animacja 3D pokazuje stojące na drodze pachołki drogowe w kształcie stożka. Kreślone są krawędzie jednego pachołka - powstaje stożek, który następnie rozkłada się na siatkę stożka.

Film dostępny pod adresem https://zpe.gov.pl/a/DbKCVKgzF
Animacja 3D pokazuje siatkę stożka, która następnie składa się w stożek. Stożek zamienia się w pachołek drogowy. Na drodze stoją cztery pachołki.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DbKCVKgzF
Pole powierzchni całkowitej stożka o promieniu podstawy i tworzącej jest równe
gdzie - pole powierzchni bocznej, - pole podstawy.
Ponieważ , , stąd
Oblicz, ile szkła zużyto na wykonanie klosza do lampy, który ma kształt stożka o wysokości i promieniu podstawy .
Aby obliczyć ile szkła użyto, obliczymy pole ;powierzchni bocznej stożka, w kształcie którego jest klosz.
, gdzie
Najpierw jednak , korzystając z twierdzenia Pitagorasa, wyznaczymy długość tworzącej odpowiedniego stożka.
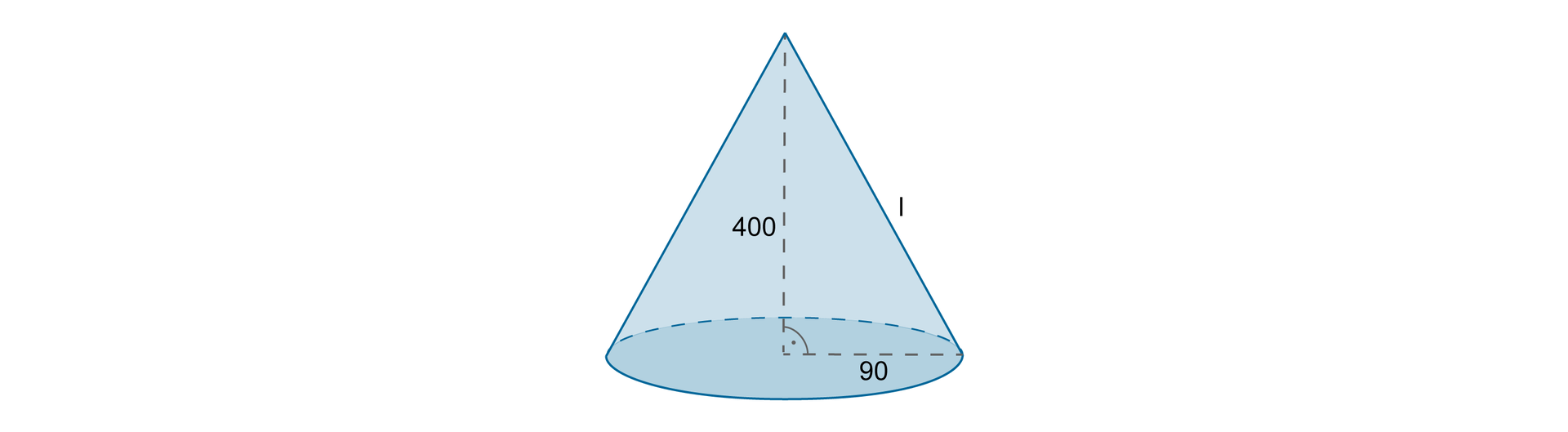
Zapisujemy wymiary stożka w decymetrach.
Obliczamy pole powierzchni bocznej stożka.
Na wykonanie klosza potrzeba szkła.
Oblicz pole powierzchni całkowitej stożka o tworzącej długości i promieniu podstawy .
Pole powierzchni całkowitej stożka obliczamy jako sumę pola powierzchni bocznej i pola podstawy.
Pole powierzchni całkowitej stożka jest równe .
Pole przekroju osiowego stożka jest równe . Pole podstawy wynosi . Oblicz pole powierzchni bocznej.
Pole podstawy stożka wynosi , zatem promień podstawy stożka jest równy .

Pole przekroju osiowego to połowa iloczynu wysokości stożka i średnicy jego podstawy. Wiedząc, że pole to jest równe , a średnica , można obliczyć wysokość stożka.
Teraz musimy jeszcze wyznaczyć długość tworzącej – korzystamy z twierdzenia Pitagorasa.
Obliczamy pole powierzchni bocznej.
Pole powierzchni bocznej stożka jest równy .
Pole powierzchni bocznej stożka jest wycinkiem koła o kącie środkowym i promieniu .
Oblicz pole powierzchni całkowitej stożka.

Obliczamy pole powierzchni bocznej stożka, jako pole wycinka koła .
Teraz wyznaczamy promień podstawy stożka.
Obliczamy pole podstawy.
Dodajemy wyznaczone wartości , obliczając pole powierzchni całkowitej stożka.
Pole powierzchni całkowitej stożka jest równe .
Trójkąt prostokątny o bokach długości obracamy wokół przeciwprostokątnej. Oblicz pole powierzchni tak powstałej bryły.
W wyniku obrotu trójkąta wokół przeciwprostokątnej powstała bryła składająca się z dwóch stożków o wspólnej podstawie. Tworzące stożków są równe przyprostokątnym trójkąta. Większy stożek ma tworzącą długości , a mniejszy ma tworzącą długości . Promienie podstaw obu stożków są równe.
Zauważmy, że promień jest wysokością obracanego trójkąta. Jego długość obliczymy, porównując pole trójkąta obliczone dwoma sposobami.
Obliczamy pole powierzchni bryły jako sumę pól powierzchni bocznych dwóch stożków.
Pole powierzchni bryły jest równe .
Podaj promień podstawy i wysokość stożka otrzymanego w wyniku obrotu trójkąta prostokątnego wokół krótszej przyprostokątnej. W trójkącie tym
długość jednej z przyprostokątnych jest równa , a przeciwprostokątna ma długość
pole jest równe , a jedna z przyprostokątnych ma długość
jeden z kątów ostrych ma miarę , a przeciwprostokątna ma długość
Oblicz pole powierzchni stożka otrzymanego w wyniku obrotu trójkąta
równobocznego o boku długości wokół prostej, na której leży jedna z wysokości trójkąta
równoramiennego wokół wysokości poprowadzonej z wierzchołka kąta między ramionami. Wysokość ta jest równa , a miara jednego z kątów .
prostokątnego równoramiennego wokół prostej, na której leży jedna z przyprostokątnych. Pole koła opisanego na tym trójkącie jest równe .
Uzupełnij.
Pole powierzchni bocznej stożka, którego wysokość jest równa ,
a pole podstawy jest równe , wynosi …
a tworząca ma długość , wynosi …
a przekrój osiowy jest trójkątem równobocznym, wynosi …
Oblicz, ile srebrnego kartonu użyto na wykonanie dekoracyjnych jednakowych choinek . Każda choinka ma kształt stożka o wysokości i promieniu podstawy . Wynik podaj z dokładnością do .
Oblicz, ile szkła użyto na wykonanie szklanego klosza do lampki nocnej. Klosz ma kształt stożka o promieniu podstawy i wysokości .
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
Podstawą stożka jest koło o polu . Pole powierzchni bocznej jest równe .
- Wysokość stożka jest o większa od średnicy podstawy.
- Pole przekroju osiowego wynosi .
- Tworząca jest o dłuższa od promienia podstawy.
Uzupełnij tabelkę.
Przekrój osiowy stożka jest trójkątem prostokątnym, którego przyprostokątna ma długość . | |||
Pole podstawy stożka | Wysokość stożka | Długość tworzącej | Pole powierzchni bocznej |
Średnica podstawy stożka jest równa , a jego wysokość . Stożek przecięto płaszczyzną równoległą do podstawy.
Średnica tak otrzymanego przekroju poprzecznego ma długość .
Oblicz pole powierzchni całkowitej stożka, który otrzymano w wyniku przekroju.

Oblicz pole powierzchni bocznej stożka, którego przekrój osiowy jest trójkątem równobocznym
o polu
o obwodzie
Pole powierzchni bocznej stożka jest równe , a pole podstawy . Oblicz wysokość stożka.
Kąt rozwarcia stożka jest równy , a tworząca jest równa . Oblicz obwód podstawy i wysokość stożka.
Powierzchnia boczna stożka jest wycinkiem koła przedstawionym na rysunku. Oblicz pole podstawy stożka.

Przekrój osiowy stożka jest trójkątem równobocznym o boku długości . Oblicz pole powierzchni bocznej stożka.
Pole powierzchni całkowitej stożka wynosi cm. Promień podstawy stożka ma długość . Oblicz długość tworzącej tego stożka.
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Przekrój stożka może być trójkątem rozwartokątnym.
- Każdy przekrój stożka jest kołem.
- Stożek jest bryłą obrotową.
Oceń prawdziwość zdania.
Istnieje stożek, którego pole powierzchni bocznej jest równe polu powierzchni jego podstawy. Odpowiedź uzasadnij.
Oblicz pole całkowite powierzchni stożka, którego powierzchnię boczną utworzono z półkola o promieniu długości .
Koło o promieniu długości rozcięto na dwa wycinki kołowe. Jeden z wycinków odpowiada kątowi środkowemu o mierze . Z każdego wycinka utworzono powierzchnię boczną stożka. Oblicz sumę długości promieni podstaw tych stożków.
Koło o promieniu długości rozcięto na dwa wycinki kołowe. Jeden z wycinków odpowiada kątowi środkowemu o mierze . Z każdego wycinka utworzono powierzchnię boczną stożka. Oblicz sumę długości promieni podstaw tych stożków.
Tworząca stożka ma długość i jest nachylona do podstawy pod kątem . Oblicz pole powierzchni całkowitej stożka.
Kąt między tworzącą i wysokością stożka ma miarę . Promień podstawy stożka ma długość . Oblicz pole powierzchni bocznej stożka.
Naszkicuj bryłę powstałą w wyniku obrotu trapezu prostokątnego wokół jego dłuższej podstawy. Oblicz powierzchnię całkowitą otrzymanej bryły, jeśli podstawy trapezu mają długości i , a wysokość trapezu ma długość .