Mnożenie sum algebraicznych

W tym materiale znajdziesz informacje na temat mnożenia sum algebraicznych, przykłady mnożenia takich sum oraz ćwiczenia sprawdzające tą umiejętność. Wykorzystasz tu swoją wiedzę na temat mnożenia jednomianów. Jeśli potrzebujesz dodatkowych informacji na temat działań na jednomianach zajrzyj do materiału Mnożenie i dzielenie sumy algebraicznej przez jednomian.

Zapamiętaj!

Aby pomnożyć przez siebie dwie sumy algebraiczne, mnożymy każdy wyraz pierwszej sumy przez każdy wyraz drugiej sumy.

Przykład 1

Pomnożymy przez siebie sumy algebraiczne:

(2 x - 3 y) (- x + 5 y) = - 2 x \cdot x + 2 x \cdot 5 y + 3 y \cdot x - 3 y \cdot 5 y =

= - 2 x^{2} + 10 x y + 3 x y - 15 y^{2} = - 2 x^{2} + 13 x y - 15 y^{2}

Przykład 2

Pomnożymy przez siebie sumy algebraiczne, wykorzystując prawa działań na potęgach o wykładniku naturalnym.

(3 a^{2} b - 5 b) (- 4 a b + 3 b) =

= - 3 a^{2} b \cdot 4 a b + 3 a^{2} b \cdot 3 b + 5 b \cdot 4 a b - 5 b \cdot 3 b =

= - 12 a^{3} b^{2} + 9 a^{2} b^{2} + 20 a b^{2} - 15 b^{2}

Przykład 3

Pomnożymy przez siebie trzy sumy algebraiczne

(2 x + 3 y) (x - 2 y) (- 3 x + y)

W pierwszej kolejności mnożymy przez siebie dwie sumy algebraiczne, a następnie wynik tego działania mnożymy przez trzecią sumę.

(2 x + 3 y) (x - 2 y) (- 3 x + y) =

= (2 x^{2} - 4 x y + 3 x y - 6 y^{2}) (- 3 x + y) =

= (2 x^{2} - x y - 6 y^{2}) (- 3 x + y) =

= - 6 x^{3} + 2 x^{2} y + 3 x^{2} y - x y^{2} + 18 x y^{2} - 6 y^{3} =

= - 6 x^{3} + 5 x^{2} y + 17 x y^{2} - 6 y^{3}

Ćwiczenie 1

Pomnóż sumy algebraiczne.

$(- 2 a + 3 b) (8 a - 5 b)$
$(4 x^{2} - 2 y) (- 3 x + 6 y^{2})$
$(5 x y - 3 x + 2 y) (- 3 x + 7 x y)$
$(- 2 a^{3} + 4 b - 3) (2 b^{2} - 5 a + 1)$
$(- 3 x y + 2 x - 3 y) (x - 5 y + 3)$
$(4 a b^{2} - 3 a^{2} + 1) (- 3 a^{2} b + 2 b - 3)$
$(2, 5 x^{2} y - 0, 4 x + 1, 2 y) (- 2 x y^{2} + 3 y - 0, 8 x)$
$(1 \frac{1}{2} a - 2 \frac{2}{3} b) (- 2 a b + \frac{3}{8})$
$(- 1 \frac{3}{4} x y + 4 y) (2 \frac{1}{2} x - 4 x y)$

R1M7SQ0301bgJ

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Pamiętaj o kolejności wykonywania działań oraz działaniach na potęgach o wykładniku naturalnym. W razie wątpliwości skorzystaj z przykładu $1$ .

$- 16 a^{2} + 34 a b - 15 b^{2}$
$- 12 x^{3} + 24 x^{2} y^{2} + 6 x y - 12 y^{3}$
$- 36 x^{2} y + 35 x^{2} y^{2} + 9 x^{2} - 6 x y + 14 x y^{2}$
$- 4 a^{3} b^{2} + 10 a^{4} - 2 a^{3} + 8 b^{3} - 20 a b + 4 b - 6 b^{2} + 15 a - 3$
$- 3 x^{2} y + 15 x y^{2} - 22 x y + 2 x^{2} + 6 x + 15 y^{2} - 9 y$
$- 12 a^{3} b^{3} + 8 a b^{3} - 12 a b^{2} + 9 a^{4} b - 9 a^{2} b + 9 a^{2} + 2 b - 3$
$- 5 x^{3} y^{3} + 8, 3 x^{2} y^{2} - 2 x^{3} y - 2, 16 x y + 0, 32 x^{2} - 2, 4 x y^{3} + 3, 6 y^{2}$
$- 3 a^{2} b + \frac{9}{16} a + 5 \frac{1}{3} a b^{2} - b$
$- 4 \frac{3}{8} x^{2} y + 7 x^{2} y^{2} + 10 x y - 16 x y^{2}$

Ćwiczenie 2

R1GwUqfzEBwNv

Zapisz iloczyn w postaci sumy. Uzupełnij poniższe równości odpowiednimi liczbami. Kliknij w lukę aby rozwinąć listę i wybierz prawidłową odpowiedź.

(\sqrt{7} - \sqrt{2}) (- 2 \sqrt{7} + 3 \sqrt{2}) =

\sqrt{6} - 5 \sqrt{2}

, 2.

- \sqrt{3} + 10 \sqrt{5}

, 3.

2 \sqrt{4} - 16 - 2 \sqrt{4} + 12 \sqrt{8}

, 4.

3 \sqrt{2} - 18 - 2 \sqrt{6} + 12 \sqrt{3}

, 5.

50 \sqrt{4} - 31 \sqrt{5}

, 6.

3 + 5 \sqrt{5}

, 7.

- 25 \sqrt{2} + 47 \sqrt{3}

, 8.

6 + 5 \sqrt{2}

, 9.

3 \sqrt{5} + 12 - 2 \sqrt{5} - 7 \sqrt{3}

, 10.

- 20 + 5 \sqrt{14}

, 11.

- 10 - 5 \sqrt{8}

, 12.

- 50 \sqrt{2} + 41 \sqrt{3}

, 13.

- \sqrt{3} - 5 \sqrt{10}

, 14.

3 - 2 \sqrt{5}

, 15.

25 + 5 \sqrt{12}

(\sqrt{5} + 2 \sqrt{6}) (- \sqrt{15} + \sqrt{2}) =

\sqrt{6} - 5 \sqrt{2}

, 2.

- \sqrt{3} + 10 \sqrt{5}

, 3.

2 \sqrt{4} - 16 - 2 \sqrt{4} + 12 \sqrt{8}

, 4.

3 \sqrt{2} - 18 - 2 \sqrt{6} + 12 \sqrt{3}

, 5.

50 \sqrt{4} - 31 \sqrt{5}

, 6.

3 + 5 \sqrt{5}

, 7.

- 25 \sqrt{2} + 47 \sqrt{3}

, 8.

6 + 5 \sqrt{2}

, 9.

3 \sqrt{5} + 12 - 2 \sqrt{5} - 7 \sqrt{3}

, 10.

- 20 + 5 \sqrt{14}

, 11.

- 10 - 5 \sqrt{8}

, 12.

- 50 \sqrt{2} + 41 \sqrt{3}

, 13.

- \sqrt{3} - 5 \sqrt{10}

, 14.

3 - 2 \sqrt{5}

, 15.

25 + 5 \sqrt{12}

(\sqrt{5} + 3) (3 \sqrt{5} - 4) =

\sqrt{6} - 5 \sqrt{2}

, 2.

- \sqrt{3} + 10 \sqrt{5}

, 3.

2 \sqrt{4} - 16 - 2 \sqrt{4} + 12 \sqrt{8}

, 4.

3 \sqrt{2} - 18 - 2 \sqrt{6} + 12 \sqrt{3}

, 5.

50 \sqrt{4} - 31 \sqrt{5}

, 6.

3 + 5 \sqrt{5}

, 7.

- 25 \sqrt{2} + 47 \sqrt{3}

, 8.

6 + 5 \sqrt{2}

, 9.

3 \sqrt{5} + 12 - 2 \sqrt{5} - 7 \sqrt{3}

, 10.

- 20 + 5 \sqrt{14}

, 11.

- 10 - 5 \sqrt{8}

, 12.

- 50 \sqrt{2} + 41 \sqrt{3}

, 13.

- \sqrt{3} - 5 \sqrt{10}

, 14.

3 - 2 \sqrt{5}

, 15.

25 + 5 \sqrt{12}

(\sqrt{6} - 2 \sqrt{2}) (\sqrt{3} - 3 \sqrt{6}) =

\sqrt{6} - 5 \sqrt{2}

, 2.

- \sqrt{3} + 10 \sqrt{5}

, 3.

2 \sqrt{4} - 16 - 2 \sqrt{4} + 12 \sqrt{8}

, 4.

3 \sqrt{2} - 18 - 2 \sqrt{6} + 12 \sqrt{3}

, 5.

50 \sqrt{4} - 31 \sqrt{5}

, 6.

3 + 5 \sqrt{5}

, 7.

- 25 \sqrt{2} + 47 \sqrt{3}

, 8.

6 + 5 \sqrt{2}

, 9.

3 \sqrt{5} + 12 - 2 \sqrt{5} - 7 \sqrt{3}

, 10.

- 20 + 5 \sqrt{14}

, 11.

- 10 - 5 \sqrt{8}

, 12.

- 50 \sqrt{2} + 41 \sqrt{3}

, 13.

- \sqrt{3} - 5 \sqrt{10}

, 14.

3 - 2 \sqrt{5}

, 15.

25 + 5 \sqrt{12}

(- 5 \sqrt{3} + 4 \sqrt{2}) (2 \sqrt{6} - 5) =

\sqrt{6} - 5 \sqrt{2}

, 2.

- \sqrt{3} + 10 \sqrt{5}

, 3.

2 \sqrt{4} - 16 - 2 \sqrt{4} + 12 \sqrt{8}

, 4.

3 \sqrt{2} - 18 - 2 \sqrt{6} + 12 \sqrt{3}

, 5.

50 \sqrt{4} - 31 \sqrt{5}

, 6.

3 + 5 \sqrt{5}

, 7.

- 25 \sqrt{2} + 47 \sqrt{3}

, 8.

6 + 5 \sqrt{2}

, 9.

3 \sqrt{5} + 12 - 2 \sqrt{5} - 7 \sqrt{3}

, 10.

- 20 + 5 \sqrt{14}

, 11.

- 10 - 5 \sqrt{8}

, 12.

- 50 \sqrt{2} + 41 \sqrt{3}

, 13.

- \sqrt{3} - 5 \sqrt{10}

, 14.

3 - 2 \sqrt{5}

, 15.

25 + 5 \sqrt{12}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RGXn8hJlemUKb1

Ćwiczenie 3

Połącz w pary.

(- 3 x y^{2} + 4 x) (4 x y - 2 y)

Możliwe odpowiedzi: 1.

- 6 x^{2} + 22 x y - 12 y^{2}

, 2.

- 6 x^{2} y + 12 x^{2} + 15 x y^{2} - 30 x y

, 3.

- 5 x^{2} y^{2} + 20 x^{3} y^{2} + 8 x y^{3} - 32 x^{2} y^{3}

, 4.

- 11 x^{2} y^{2} + 12 x^{3} y + 2, 5 x y^{3}

, 5.

- 12 x^{2} y^{3} + 6 x y^{3} + 16 x^{2} y - 8 x y

(\sqrt{2} x - 3 \sqrt{2} y) (- \sqrt{18} x + \sqrt{8} y)

Możliwe odpowiedzi: 1.

- 6 x^{2} + 22 x y - 12 y^{2}

, 2.

- 6 x^{2} y + 12 x^{2} + 15 x y^{2} - 30 x y

, 3.

- 5 x^{2} y^{2} + 20 x^{3} y^{2} + 8 x y^{3} - 32 x^{2} y^{3}

, 4.

- 11 x^{2} y^{2} + 12 x^{3} y + 2, 5 x y^{3}

, 5.

- 12 x^{2} y^{3} + 6 x y^{3} + 16 x^{2} y - 8 x y

(1, 2 x y - 0, 5 y^{2}) (- 5 x y + 10 x^{2})

Możliwe odpowiedzi: 1.

- 6 x^{2} + 22 x y - 12 y^{2}

, 2.

- 6 x^{2} y + 12 x^{2} + 15 x y^{2} - 30 x y

, 3.

- 5 x^{2} y^{2} + 20 x^{3} y^{2} + 8 x y^{3} - 32 x^{2} y^{3}

, 4.

- 11 x^{2} y^{2} + 12 x^{3} y + 2, 5 x y^{3}

, 5.

- 12 x^{2} y^{3} + 6 x y^{3} + 16 x^{2} y - 8 x y

(1 \frac{1}{2} x - 3 \frac{3}{4} y) (- 4 x y + 8 x)

Możliwe odpowiedzi: 1.

- 6 x^{2} + 22 x y - 12 y^{2}

, 2.

- 6 x^{2} y + 12 x^{2} + 15 x y^{2} - 30 x y

, 3.

- 5 x^{2} y^{2} + 20 x^{3} y^{2} + 8 x y^{3} - 32 x^{2} y^{3}

, 4.

- 11 x^{2} y^{2} + 12 x^{3} y + 2, 5 x y^{3}

, 5.

- 12 x^{2} y^{3} + 6 x y^{3} + 16 x^{2} y - 8 x y

(2, 5 x^{2} y^{2} - 4 x y^{3}) (- 2 + 8 x)

Możliwe odpowiedzi: 1.

- 6 x^{2} + 22 x y - 12 y^{2}

, 2.

- 6 x^{2} y + 12 x^{2} + 15 x y^{2} - 30 x y

, 3.

- 5 x^{2} y^{2} + 20 x^{3} y^{2} + 8 x y^{3} - 32 x^{2} y^{3}

, 4.

- 11 x^{2} y^{2} + 12 x^{3} y + 2, 5 x y^{3}

, 5.

- 12 x^{2} y^{3} + 6 x y^{3} + 16 x^{2} y - 8 x y

Połącz w pary.

$(- 3 x y^{2} + 4 x) (4 x y - 2 y)$
$(\sqrt{2} x - 3 \sqrt{2} y) (- \sqrt{18} x + \sqrt{8} y)$
$(1, 2 x y - 0, 5 y^{2}) (- 5 x y + 10 x^{2})$
$(1 \frac{1}{2} x - 3 \frac{3}{4} y) (- 4 x y + 8 x)$
$(2, 5 x^{2} y^{2} - 4 x y^{3}) (- 2 + 8 x)$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RBGamU44ZxEng2

Ćwiczenie 4

Uzupełnij poniższe równości odpowiednimi jednomianami. Kliknij w lukę aby wyświetlić listę rozwijalną i wybierz właściwą odpowiedź.

(2 a b - 3 b^{2}) (- 2, 5 a + 5 b^{2}) =

5 \frac{1}{4} a^{4} b^{2}

, 2.

- 16, 5 x y^{2}

, 3.

- 3 x y^{2}

, 4.

a^{2} b

, 5.

- 2 x

, 6.

3 b

, 7.

- 5 a^{2} b

, 8.

2 x

, 9.

4 x^{2} y^{3}

, 10.

7 x y^{2}

, 11.

3 b^{2}

+ 10 a b^{3} + 7, 5 a b^{2} - 15 b^{4}

(- 4 x y + 5 x) (2 x^{2} y - x y^{2}) = - 8 x^{3} y^{2} +

5 \frac{1}{4} a^{4} b^{2}

, 2.

- 16, 5 x y^{2}

, 3.

- 3 x y^{2}

, 4.

a^{2} b

, 5.

- 2 x

, 6.

3 b

, 7.

- 5 a^{2} b

, 8.

2 x

, 9.

4 x^{2} y^{3}

, 10.

7 x y^{2}

, 11.

3 b^{2}

+ 10 x^{3} y - 5 x^{2} y^{2}

(1, 5 a^{3} b - 2, 2 a b^{2}) (- 4 a + 3, 5 a b) = - 6 a^{4} b +

5 \frac{1}{4} a^{4} b^{2}

, 2.

- 16, 5 x y^{2}

, 3.

- 3 x y^{2}

, 4.

a^{2} b

, 5.

- 2 x

, 6.

3 b

, 7.

- 5 a^{2} b

, 8.

2 x

, 9.

4 x^{2} y^{3}

, 10.

7 x y^{2}

, 11.

3 b^{2}

+ 8, 8 a^{2} b^{2} - 7, 7 a^{2} b^{3}

(1 \frac{1}{2} x - 4, 5 y^{2}) (- 2 y^{2} + 3 x) =

5 \frac{1}{4} a^{4} b^{2}

, 2.

- 16, 5 x y^{2}

, 3.

- 3 x y^{2}

, 4.

a^{2} b

, 5.

- 2 x

, 6.

3 b

, 7.

- 5 a^{2} b

, 8.

2 x

, 9.

4 x^{2} y^{3}

, 10.

7 x y^{2}

, 11.

3 b^{2}

+ 4, 5 x^{2} + 9 y^{4} - 13, 5 x y^{2} =

=

5 \frac{1}{4} a^{4} b^{2}

, 2.

- 16, 5 x y^{2}

, 3.

- 3 x y^{2}

, 4.

a^{2} b

, 5.

- 2 x

, 6.

3 b

, 7.

- 5 a^{2} b

, 8.

2 x

, 9.

4 x^{2} y^{3}

, 10.

7 x y^{2}

, 11.

3 b^{2}

+ 4, 5 x^{2} + 9 y^{4}

(5, 5 x y - 1, 2 y) (

5 \frac{1}{4} a^{4} b^{2}

, 2.

- 16, 5 x y^{2}

, 3.

- 3 x y^{2}

, 4.

a^{2} b

, 5.

- 2 x

, 6.

3 b

, 7.

- 5 a^{2} b

, 8.

2 x

, 9.

4 x^{2} y^{3}

, 10.

7 x y^{2}

, 11.

3 b^{2}

+ 10 y) = - 11 x^{2} y + 55 x y^{2} + 2, 4 x y - 12 y^{2}

(4 a^{2} b^{2} +

5 \frac{1}{4} a^{4} b^{2}

, 2.

- 16, 5 x y^{2}

, 3.

- 3 x y^{2}

, 4.

a^{2} b

, 5.

- 2 x

, 6.

3 b

, 7.

- 5 a^{2} b

, 8.

2 x

, 9.

4 x^{2} y^{3}

, 10.

7 x y^{2}

, 11.

3 b^{2}

) (- 2 a b + 5 a) = - 8 a^{3} b^{3} + 20 a^{3} b^{2} - 6 a b^{3} + 15 a b^{2}

Przeciągnij i upuść jednomiany tak, aby podane równości były prawdziwe.

$5 \frac{1}{4} a^{4} b^{2}$ , $- 2 x$ , $- 3 x y^{2}$ , $4 x^{2} y^{3}$ , $3 b^{2}$ , $3 b$ , $- 5 a^{2} b$ , $- 16, 5 x y^{2}$

a) $(2 a b - 3 b^{2}) (- 2, 5 a + 5 b^{2}) =$ ................ $+ 10 a b^{3} + 7, 5 a b^{2} - 15 b^{4}$
b) $(- 4 x y + 5 x) (2 x^{2} y - x y^{2}) = - 8 x^{3} y^{2} +$ ................ $+ 10 x^{3} y - 5 x^{2} y^{2}$
c) $(1, 5 a^{3} b - 2, 2 a b^{2}) (- 4 a + 3, 5 a b) = - 6 a^{4} b +$ ................ $+ 8, 8 a^{2} b^{2} - 7, 7 a^{2} b^{3}$
d) $(1 \frac{1}{2} x - 4, 5 y^{2}) (- 2 y^{2} + 3 x) =$ ................ $+ 4, 5 x^{2} + 9 y^{4} - 13, 5 x y^{2} =$ ................ $+ 4, 5 x^{2} + 9 y^{4}$
e) $(5, 5 x y - 1, 2 y) ($ ................ $+ 10 y) = - 11 x^{2} y + 55 x y^{2} + 2, 4 x y - 12 y^{2}$
f) $(4 a^{2} b^{2} +$ ................ $) (- 2 a b + 5 a) = - 8 a^{3} b^{3} + 20 a^{3} b^{2} - 6 a b^{3} + 15 a b^{2}$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 5

REAeXSV63LyAY

Uzupełnij poniższe równości odpowiednimi wyrażeniami. Kliknij w lukę aby rozwinąć listę i wybierz właściwą odpowiedź.

(2 a - 3) (a + 1) (- 3 a + 4)

=

- 10 x^{3} + 33 x^{2} - 5 x - 12

, 2.

12 a b^{2} - 9 b^{3} + 4 a^{3} + 6 a^{3} b

, 3.

- 46 x^{2} y - 40 x y^{2} + 20 x^{3} - 6 y^{3}

, 4.

9 a b^{2} - 9 b^{3} - 4 a^{3} + 4 a^{2} b

, 5.

- 6 a^{2} - 11 a^{2} + 5 a + 10

, 6.

15 x^{3} + 33 x^{3} + 25 x - 12

, 7.

6 a^{3} + 11 a^{3} - 5 a - 14

, 8.

- 5 x^{2} - 33 x^{3} - 10 x + 12

, 9.

- 6 a^{3} + 11 a^{2} + 5 a - 12

, 10.

18 a b^{3} + 9 b^{2} - 4 a^{2} - 2 a^{3} b

, 11.

- 44 x^{2} y + 40 x y^{3} + 20 x^{3} + 6 y^{2}

, 12.

48 x^{3} y - 40 x y^{3} - 20 x^{2} - 6 y^{2}

(4 x + 2 y) (- 5 x - y) (3 y - x)

=

- 10 x^{3} + 33 x^{2} - 5 x - 12

, 2.

12 a b^{2} - 9 b^{3} + 4 a^{3} + 6 a^{3} b

, 3.

- 46 x^{2} y - 40 x y^{2} + 20 x^{3} - 6 y^{3}

, 4.

9 a b^{2} - 9 b^{3} - 4 a^{3} + 4 a^{2} b

, 5.

- 6 a^{2} - 11 a^{2} + 5 a + 10

, 6.

15 x^{3} + 33 x^{3} + 25 x - 12

, 7.

6 a^{3} + 11 a^{3} - 5 a - 14

, 8.

- 5 x^{2} - 33 x^{3} - 10 x + 12

, 9.

- 6 a^{3} + 11 a^{2} + 5 a - 12

, 10.

18 a b^{3} + 9 b^{2} - 4 a^{2} - 2 a^{3} b

, 11.

- 44 x^{2} y + 40 x y^{3} + 20 x^{3} + 6 y^{2}

, 12.

48 x^{3} y - 40 x y^{3} - 20 x^{2} - 6 y^{2}

(2 a + 3 b) (3 b - 2 a) (a - b)

=

- 10 x^{3} + 33 x^{2} - 5 x - 12

, 2.

12 a b^{2} - 9 b^{3} + 4 a^{3} + 6 a^{3} b

, 3.

- 46 x^{2} y - 40 x y^{2} + 20 x^{3} - 6 y^{3}

, 4.

9 a b^{2} - 9 b^{3} - 4 a^{3} + 4 a^{2} b

, 5.

- 6 a^{2} - 11 a^{2} + 5 a + 10

, 6.

15 x^{3} + 33 x^{3} + 25 x - 12

, 7.

6 a^{3} + 11 a^{3} - 5 a - 14

, 8.

- 5 x^{2} - 33 x^{3} - 10 x + 12

, 9.

- 6 a^{3} + 11 a^{2} + 5 a - 12

, 10.

18 a b^{3} + 9 b^{2} - 4 a^{2} - 2 a^{3} b

, 11.

- 44 x^{2} y + 40 x y^{3} + 20 x^{3} + 6 y^{2}

, 12.

48 x^{3} y - 40 x y^{3} - 20 x^{2} - 6 y^{2}

(5 x - 4) (- x + 3) (2 x + 1)

=

- 10 x^{3} + 33 x^{2} - 5 x - 12

, 2.

12 a b^{2} - 9 b^{3} + 4 a^{3} + 6 a^{3} b

, 3.

- 46 x^{2} y - 40 x y^{2} + 20 x^{3} - 6 y^{3}

, 4.

9 a b^{2} - 9 b^{3} - 4 a^{3} + 4 a^{2} b

, 5.

- 6 a^{2} - 11 a^{2} + 5 a + 10

, 6.

15 x^{3} + 33 x^{3} + 25 x - 12

, 7.

6 a^{3} + 11 a^{3} - 5 a - 14

, 8.

- 5 x^{2} - 33 x^{3} - 10 x + 12

, 9.

- 6 a^{3} + 11 a^{2} + 5 a - 12

, 10.

18 a b^{3} + 9 b^{2} - 4 a^{2} - 2 a^{3} b

, 11.

- 44 x^{2} y + 40 x y^{3} + 20 x^{3} + 6 y^{2}

, 12.

48 x^{3} y - 40 x y^{3} - 20 x^{2} - 6 y^{2}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1012djMrjzxQ2

Ćwiczenie 6

Uzupełnij poniższe równości odpowiednimi jednomianami. Kliknij w lukę aby rozwinąć listę i wybierz właściwą odpowiedź.

(- 5 y + 1) (2 y - 3) (y + 2) = - 10 y^{3} -

7

, 2.

20 a^{2} b

, 3.

5 x y

, 4.

23 x y

, 5.

33 x y

, 6.

28 a^{2} b

, 7.

3

, 8.

28 x y

y^{2} + 31 y - 6

(3 x + 2 y) (- x - 3 y) (x - 3) = - 3 x^{3} + 9 x^{2} - 11 x^{2} y +

7

, 2.

20 a^{2} b

, 3.

5 x y

, 4.

23 x y

, 5.

33 x y

, 6.

28 a^{2} b

, 7.

3

, 8.

28 x y

- 6 x y^{2} + 18 y^{2}

(- 2 a + 4 b) (a - b) (4 a - 2 b) = - 8 a^{3} +

7

, 2.

20 a^{2} b

, 3.

5 x y

, 4.

23 x y

, 5.

33 x y

, 6.

28 a^{2} b

, 7.

3

, 8.

28 x y

- 28 a b^{2} + 8 b^{3}

(7 x - 3) (3 y + 2) (x - y) = 21 x^{2} y - 21 x y^{2} + 14 x^{2} -

7

, 2.

20 a^{2} b

, 3.

5 x y

, 4.

23 x y

, 5.

33 x y

, 6.

28 a^{2} b

, 7.

3

, 8.

28 x y

+ 9 y^{2} - 6 x + 6 y

Przeciągnij i upuść jednomiany tak, aby podane równości były prawdziwe.

$28 a^{2} b$ , $20 a^{2} b$ , $3$ , $5 x y$ , $33 x y$ , $7$ , $23 x y$

a) $(- 5 y + 1) (2 y - 3) (y + 2) = - 10 y^{3} -$ ............ $y^{2} + 31 y - 6$
b) $(3 x + 2 y) (- x - 3 y) (x - 3) = - 3 x^{3} + 9 x^{2} - 11 x^{2} y +$ ............ $- 6 x y^{2} + 18 y^{2}$
c) $(- 2 a + 4 b) (a - b) (4 a - 2 b) = - 8 a^{3} +$ ............ $- 28 a b^{2} + 8 b^{3}$
d) $(7 x - 3) (3 y + 2) (x - y) = 21 x^{2} y - 21 x y^{2} + 14 x^{2} -$ ............ $+ 9 y^{2} - 6 x + 6 y$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RvIBwabeGMGSW2

Ćwiczenie 7

$x^{3} + 3 x^{2} - 3 x - 1$
$x^{3} - 3 x^{2} - 3 x + 1$
$x^{3} - 3 x^{2} + 3 x - 1$
$x^{3} - 3 x^{2} + 3 x + 1$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RjTpqod8EDi8D2

Ćwiczenie 8

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 9

R7kbK4VeMsdGJ

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 10

Zapisz w postaci wyrażenia algebraicznego pole poniższego trapezu.

R1SiftV3oAar41

Rysunek przedstawia trapez, którego podstawa górna ma długość a-3b, podstawa dolna 2a+1, a wysokość wynosi a-1. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1FRH6nIcGLEQ

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 11

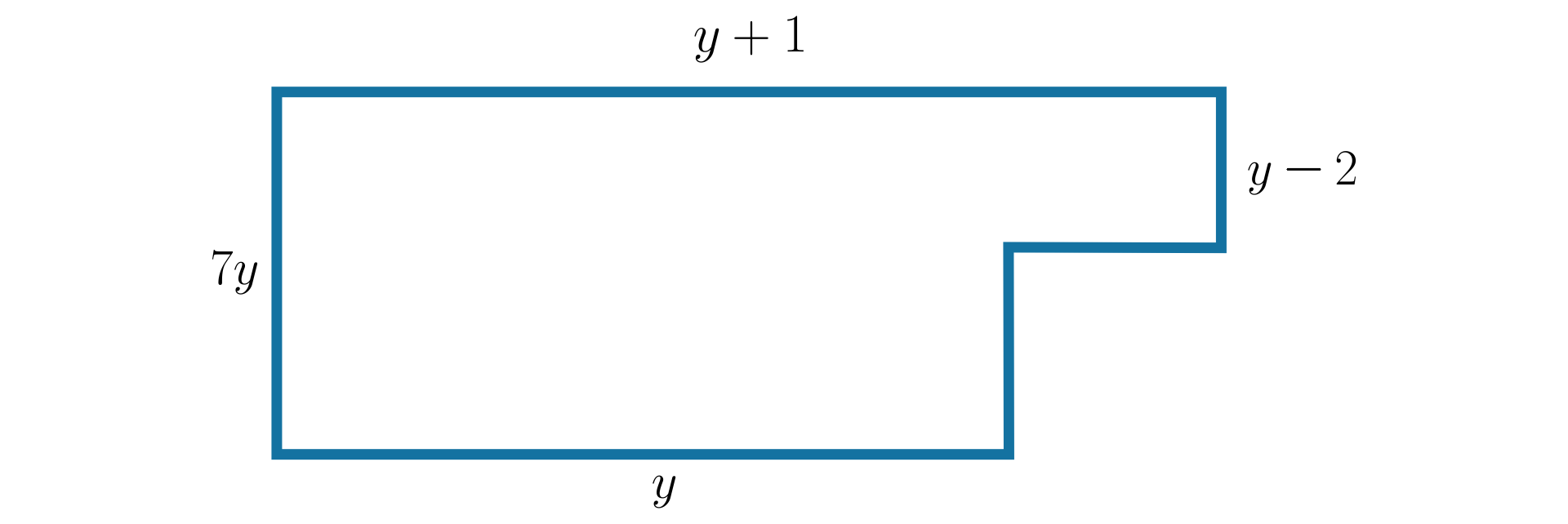
Jakie wyrażenie algebraiczne opisuje pole wielokąta przedstawionego na rysunku poniżej?

RKa9Fa1T0IMCL1

Rysunek przedstawia wielokąt będący prostokątem, który ma wycięty mały prostokąt przy dolnym prawym wierzchołku. Lewy pionowy bok figury ma długość siedem razy igrek. Górny poziomy bok figury ma długość y+1. Następnie prawy pionowy bok figury ma długość y-2, następnie mamy poziome wcięcie i dalej pionowy bok. Oba nie mają opisanej długości. Następnym bokiem jest poziomy dolny bok o długości igrek. Lewy pionowy bok ma długość równą sumie dwóch krótszych pionowych prawych boków. Górny bok ma długość równą długości dwóch krótszych dolnych boków. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RwxD12d2BInPx

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 12

RsDCgwMhZKoxL

W poniedziałek w księgarni sprzedano

x

książek, z których każda kosztowała

y

złotych. Następnego dnia cenę książki obniżono o

5 zł

i wtedy sprzedano o

20

książek więcej niż pierwszego dnia. Zapisz w postaci wyrażenia algebraicznego, ile pieniędzy uzyskała księgarnia ze sprzedaży książek w ciągu dwóch dni. Uzupełnij poniższe zdanie, przeciągając w lukę odpowiednie z podanych wyrażenie algebraiczne. Odpowiedź: Księgarnia uzyskała 1.

2 x y + 30 y + 5 x - 100

, 2.

2 x y + 20 y - 5 x - 100

, 3.

8 x y - 25 y - 15 x - 110

, 4.

4 x y + 10 y - 10 x + 90

pieniędzy.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 13

RRhKCuBRXot9i

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 14

Prostokątny obraz umieszczono w ramie. Obraz wraz z ramą ma długość $3 x + 20 cm$ i szerokość $2 x + 15 cm$ . Jakie jest pole powierzchni obrazu, jeżeli szerokość ramy wynosi $18 cm$ ?

Uzupełnij poniższe zdanie odpowiednim wyrażeniem algebraicznym. Kliknij w lukę aby rozwinąć listę i wybierz prawidłową odpowiedź.

RoiJrBvBvvpfr1

Rysunek obrazu w ramie. Obraz zawieszony jest na ścianie, widnieją na nim ośnieżone szczyty gór. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RdRttkGvy10hl

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 15

RkfQiAI381xap

Długości krawędzi prostopadłościanu wychodzących z jednego wierzchołka wynoszą

2 x

3 y

z

. Jaką objętość będzie miał prostopadłościan, którego każda z krawędzi ma długość o

1

większą? Uzupełnij poniższe zdanie odpowiednim wyrażeniem algebraicznym. Kliknij w lukę aby rozwinąć listę i wybierz prawidłową odpowiedź. Odpowiedź: Objętość prostopadłościanu wynosi 1.

3 x y z + 6 x y - 8 x z - 8 x + 9 y z + 3 y + z + 1

, 2.

6 x y z + 6 x y + 2 x z + 2 x + 3 y z + 3 y + z + 1

, 3.

9 x y z + 6 x y + 4 x z + 2 x + 3 y z + 6 y - z - 1

, 4.

12 x y z + 6 x y - 2 x z + 4 x + 6 y z + 3 y + z - 1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 16

RCpDERGK6Ccjr

Zapisz w postaci wyrażenia algebraicznego. Uzupełnij poniższe zdania, przeciągając w luki odpowiednie z podanych wyrażeń. Iloczyn trzech kolejnych liczb naturalnych, z których największa jest równa

n

to 1.

6 n^{3} + 10 n^{2} + 4

, 2.

8 n^{3} + 24 n^{2} + 16 n

, 3.

4 n^{2} + 8 n^{2} + 3

, 4.

n^{3} - 9 n^{2} + 4 n

, 5.

8 n^{4} + 6 n^{2} + 5

, 6.

6 n^{4} - 26 n^{2} + 14 n

, 7.

n^{3} - 3 n^{2} + 2 n

, 8.

n^{4} - 6 n^{3} + 3 n

, 9.

12 n^{6} + 21 n^{2} - 12 n

.
Iloczyn dwóch kolejnych liczb nieparzystych, z których mniejsza jest równa

2 n + 1

to 1.

6 n^{3} + 10 n^{2} + 4

, 2.

8 n^{3} + 24 n^{2} + 16 n

, 3.

4 n^{2} + 8 n^{2} + 3

, 4.

n^{3} - 9 n^{2} + 4 n

, 5.

8 n^{4} + 6 n^{2} + 5

, 6.

6 n^{4} - 26 n^{2} + 14 n

, 7.

n^{3} - 3 n^{2} + 2 n

, 8.

n^{4} - 6 n^{3} + 3 n

, 9.

12 n^{6} + 21 n^{2} - 12 n

.
Iloczyn trzech kolejnych liczb parzystych, z których najmniejsza jest równa

2 n

to 1.

6 n^{3} + 10 n^{2} + 4

, 2.

8 n^{3} + 24 n^{2} + 16 n

, 3.

4 n^{2} + 8 n^{2} + 3

, 4.

n^{3} - 9 n^{2} + 4 n

, 5.

8 n^{4} + 6 n^{2} + 5

, 6.

6 n^{4} - 26 n^{2} + 14 n

, 7.

n^{3} - 3 n^{2} + 2 n

, 8.

n^{4} - 6 n^{3} + 3 n

, 9.

12 n^{6} + 21 n^{2} - 12 n

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 17

Piaskownica jest prostokątem o długości $2 a$ metrów $b$ centymetrów i szerokości $3 b$ metrów $a$ centymetrów. Ile metrów kwadratowych ma pole powierzchni piaskownicy? Uzupełnij poniższe zdanie odpowiednim wyrażeniem algebraicznym. Kliknij w lukę aby rozwinąć listę i wybierz prawidłową odpowiedź.

R1NitU1zCsJ1K1

Ilustracja piaskownicy z rozrzuconymi w środku zabawkami. Piaskownica zrobiona jest z drewnianych desek. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R10J6dn92m1j0

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.