Odległość na osi liczbowej
Zaznaczmy na osi liczbowej liczby, które są większe od .
RxKsu2QDIhEM11  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Liczby te spełniają nierówność . Jeżeli nierówność jest ostra, tzn. spełniona tylko przez liczby większe od trzech, wtedy kółko jest niezamalowane.
Zaznaczmy na osi liczbowej liczby, które są mniejsze od .
R1cz2v0xm5j6t1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Liczby te spełniają nierówność .
Zaznaczmy na osi liczbowej liczby, które są większe lub równe od .
RctaQlzMF1nbt1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Liczby te spełniają nierówność . Jeżeli nierówność jest nieostra, tzn. spełniona przez liczby większe lub równe jeden, wtedy kółko jest zamalowane.
Zaznaczmy na osi liczbowej liczby, które są mniejsze lub równe .
R1YlnzkVKnKJ01  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Liczby te spełniają nierówność .
Jeżeli o pewnej liczbie wiemy, że jest większa od i mniejsza od , to znaczy, że liczba spełnia warunek: .
Wszystkie liczby spełniające ten warunek możemy zaznaczyć na osi liczbowej.

Jeżeli o pewnej liczbie wiemy, że jest większa lub równa od i mniejsza od , to znaczy, że liczba spełnia warunek: .
Wszystkie liczby spełniające ten warunek możemy zaznaczyć na osi liczbowej.

Jeżeli o pewnej liczbie wiemy, że jest większa od i mniejsza lub równa od , to znaczy, że liczba spełnia warunek: .
Wszystkie liczby spełniające ten warunek możemy zaznaczyć na osi liczbowej.

Jeżeli o pewnej liczbie wiemy, że jest większa lub równa od i mniejsza lub równa od , to znaczy, że liczba spełnia warunek: .
Wszystkie liczby spełniające ten warunek możemy zaznaczyć na osi liczbowej.

Zaznaczmy na osi liczbowej liczby i .
R6jjmMOjIb3gd1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Na osi liczbowej między i mieści się odcinków jednostkowych. a więc odległość między liczbami i 9 wynosi . ponieważ
Zaznaczmy na osi liczbowej liczby i .
RR3oGiUY3Ey0D1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Na osi liczbowej między i mieści się odcinków jednostkowych, a więc odległość między liczbami i wynosi , ponieważ
Zaznaczmy na osi liczbowej liczby i .
RFmCF4QqiP28Z1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Na osi liczbowej między i mieści się odcinków jednostkowych a więc odległość między liczbami i wynosi , ponieważ
Obliczmy odległość między liczbami i .
Ponieważ więc aby obliczyć szukaną odległość musimy od odjąć .
A zatem odległość między liczbami i wynosi jednostek.
Możemy również policzyć wartość bezwzględną różnicy liczba i , wtedy nie ma znaczenia, czy od większej odejmujemy mniejszą, czy odwrotnie.
Odległość między liczbami i jest równa lub .
Obliczmy odległość na osi liczbowej między liczbami i .

Film dostępny na portalu epodreczniki.pl
Animacja przedstawia zaznaczoną na osi liczbowej odległość między liczbami 9 oraz dwa i jedna druga. Zapis: wartość bezwzględna z liczby (9 – dwa i jedna druga) = wartość bezwzględna z liczby (dwa i jedna druga -9) = sześć i jedna druga.
Ponieważ więc aby obliczyć szukaną odległość musimy od odjąć .
A zatem odległość między liczbami i wynosi .
Możemy również obliczyć wartość bezwzględną różnicy liczb i . Wówczas nie ma znaczenia, czy od liczby większej odejmujemy mniejszą, czy odwrotnie.
Odległość między liczbami i jest równa lub .
Oblicz odległość na osi liczbowej liczb i .

Film dostępny na portalu epodreczniki.pl
Animacja przedstawia zaznaczoną na osi liczbowej odległość między liczbami -1 oraz siedem i jedna druga. Zapis: wartość bezwzględna z liczby [siedem i jedna druga -(-1)] = wartość bezwzględna z liczby (-1, siedem i jedna druga) = osiem i jedna druga.
Odległość między dwiema dowolnymi liczbami na osi liczbowej jest równa długości odcinka łączącego punkty odpowiadające tym liczbom.
Aby obliczyć odległość na osi liczbowej między dwiema liczbami, należy od większej odjąć mniejszą.
Jeżeli nie wiemy, która z liczb i jest większa, to aby obliczyć odległość między tymi liczbami na osi liczbowej wystarczy obliczyć lub.

Film dostępny na portalu epodreczniki.pl
Animacja

Film dostępny na portalu epodreczniki.pl
Animacja
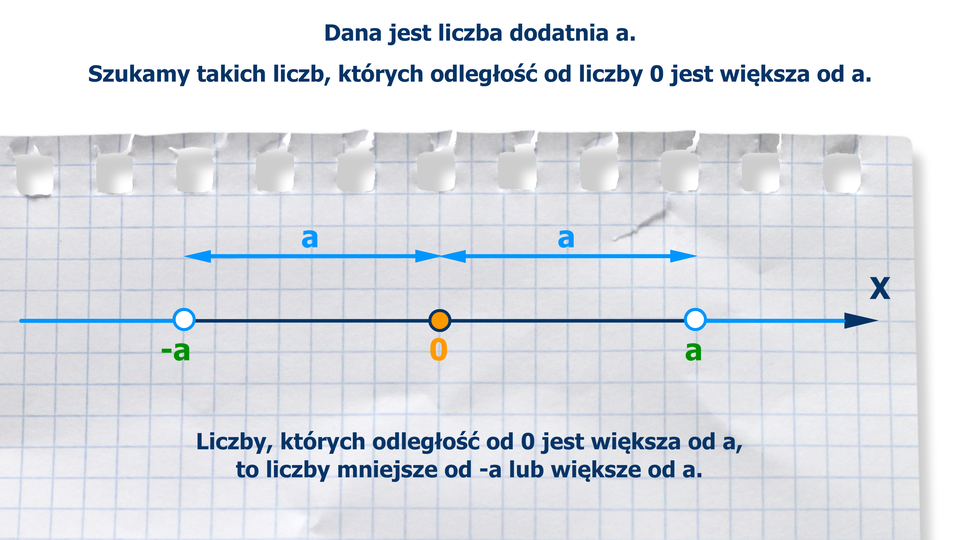
Film dostępny na portalu epodreczniki.pl
Animacja

Film dostępny na portalu epodreczniki.pl
Animacja
Oblicz.
Oblicz.
Wybierz.
<, <, <, >, >, >, >, =, <, >, =, <, =, <, <, >, >, =, =, <, =, >, =, =
............
............
............
............
............
............
............
............
Liczb naturalnych spełniających warunek
- są
- jest
- jest
- jest nieskończenie wiele
Wszystkie liczby całkowite spełniające warunek to
Jeżeli to zachodzi warunek
- lub
Oblicz jeżeli
i
i
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Wartość bezwzględna każdej liczby jest liczbą dodatnią.
- Liczby przeciwne mają taką samą wartość bezwzględną.
- Wartość bezwzględna liczby jest równa liczbie do niej przeciwnej.
- Liczby odwrotne mają przeciwne wartości bezwzględne.
Połącz w pary.
<span aria-label="x, mniejszy niż, pięć" role="math"><math><mi>x</mi><mo><</mo><mn>5</mn></math></span>, <span aria-label="x, większy równy, minus, pięć" role="math"><math><mi>x</mi><mo>≥</mo><mo>-</mo><mn>5</mn></math></span>, <span aria-label="x, większy równy, zero" role="math"><math><mi>x</mi><mo>≥</mo><mn>0</mn></math></span>, <span aria-label="x, mniejszy niż, zero" role="math"><math><mi>x</mi><mo><</mo><mn>0</mn></math></span>, <span aria-label="x, mniejszy równy, minus, pięć" role="math"><math><mi>x</mi><mo>≤</mo><mo>-</mo><mn>5</mn></math></span>, <span aria-label="x, większy równy, pięć" role="math"><math><mi>x</mi><mo>≥</mo><mn>5</mn></math></span>
| liczba x jest mniejsza od 5 | |
| liczba x jest większa lub równa −5 | |
| liczba x jest nie mniejsza od 5 | |
| liczba x jest nie większa od −5 | |
| liczba x jest ujemna | |
| liczba x jest nieujemna |
Zaznacz na osi liczbowej wszystkie liczby spełniające dany warunek.
Podaj warunek, jaki spełniają liczby zaznaczone na osi liczbowej.
R1AdhDP8fTouz1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R6WpeuqTeVOpJ1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Rju6DlgyQff6K1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R1FkjDRjviL9u1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Zaznacz na osi liczbowej zbiór liczb spełniających dany warunek.
Określ, jaki warunek spełniają liczby zaznaczone na osi liczbowej.
R1aGnEQMvU2in1 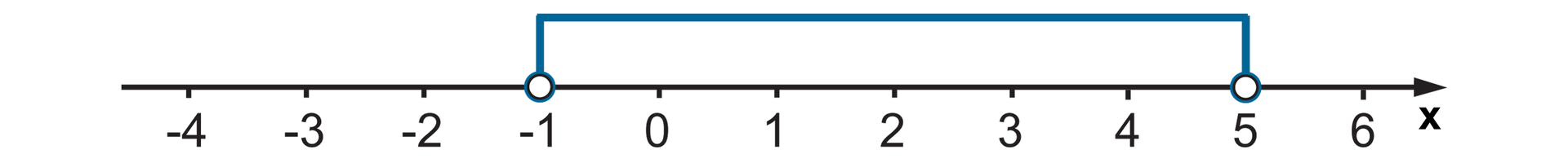 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.ReUl2sBvOVA871  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.RcEoG1p9GkoYU1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R1FY18X3vaYA41  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Wymień, gdy jest to możliwe, wszystkie liczby spełniające dany warunek.
i jest liczbą naturalną
i jest liczbą całkowitą dodatnią
i jest liczbą całkowitą
i jest liczbą całkowitą ujemną
i jest liczbą naturalną
i jest liczbą wymierną
Zaznacz na osi liczbowej wszystkie liczby spełniające podany warunek.
Zaznacz na osi liczbowej wszystkie liczby spełniające podany warunek.
Oblicz , jeżeli .
Znajdź odległość na osi liczbowej między punktami: i , i , i , i , i , i .
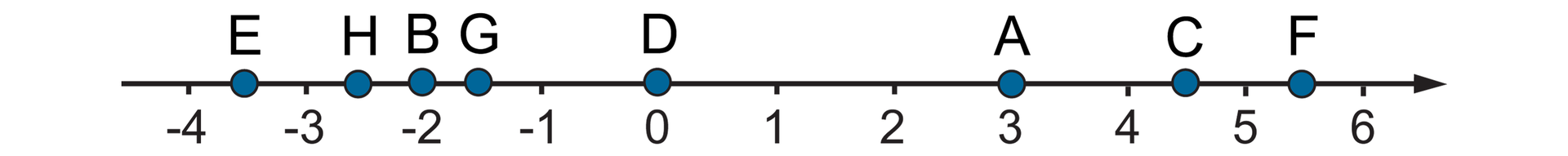
Uzupełnij zdania.

Odległość punktu od punktu jest odległości punktu od punktu .
Odległość punktu od punktu jest równa .
Odległość punktu od punktu jest o większa od odległości punktu od punktu .
Odległość punktu od punktu jest razy większa od odległości punktu od punktu .
Odległość punktu od punktu jest równa podwojonej sumie odległości punktu od punktu i punktu od punktu .
Liczby leżące na osi liczbowej w takiej samej odległości od liczby to
- i
- i
- i
- i
Liczba leżąca na osi liczbowej w takiej samej odległości od i to
Zbiór liczb leżących na osi liczbowej w odległości nie większej niż od liczby opiszemy nierównością
Oblicz odległość między danymi liczbami, a następnie przeciągnij i upuść.
, , , , ,
a) i ............................
b) i ............................
c) i ............................
d) i ............................
e) i ............................
f) i ............................