Określanie monotoniczności funkcji na podstawie jej wykresu - ćwiczenia. Cześć I
Podczas badania przebiegu zmienności funkcji określamy własności tej funkcji, w tym jej monotoniczność na całej dziedzinie albo na przedziałach. W tym materiale:
określisz monotoniczność funkcji na podstawie jej wykresu,
wskażesz wykres funkcji o podanej monotoniczności.
Jeżeli potrzebujesz przypomnieć sobie pojęcia związane z monotonicznością funkcji, skorzystaj z lekcji: Monotoniczność funkcjiMonotoniczność funkcji. Do ponownego przeanalizowania przykładów odpowiednia będzie lekcja Odczytywanie przedziałów monotoniczności funkcji z wykresu. PrzykładyOdczytywanie przedziałów monotoniczności funkcji z wykresu. Przykłady.
Na rysunku przedstawiony jest wykres funkcji .

Jest to funkcja: Możliwe odpowiedzi: 1. rosnąca, 2. malejąca, 3. stała, 4. niemonotoniczna
Na rysunku przedstawiony jest wykres funkcji .
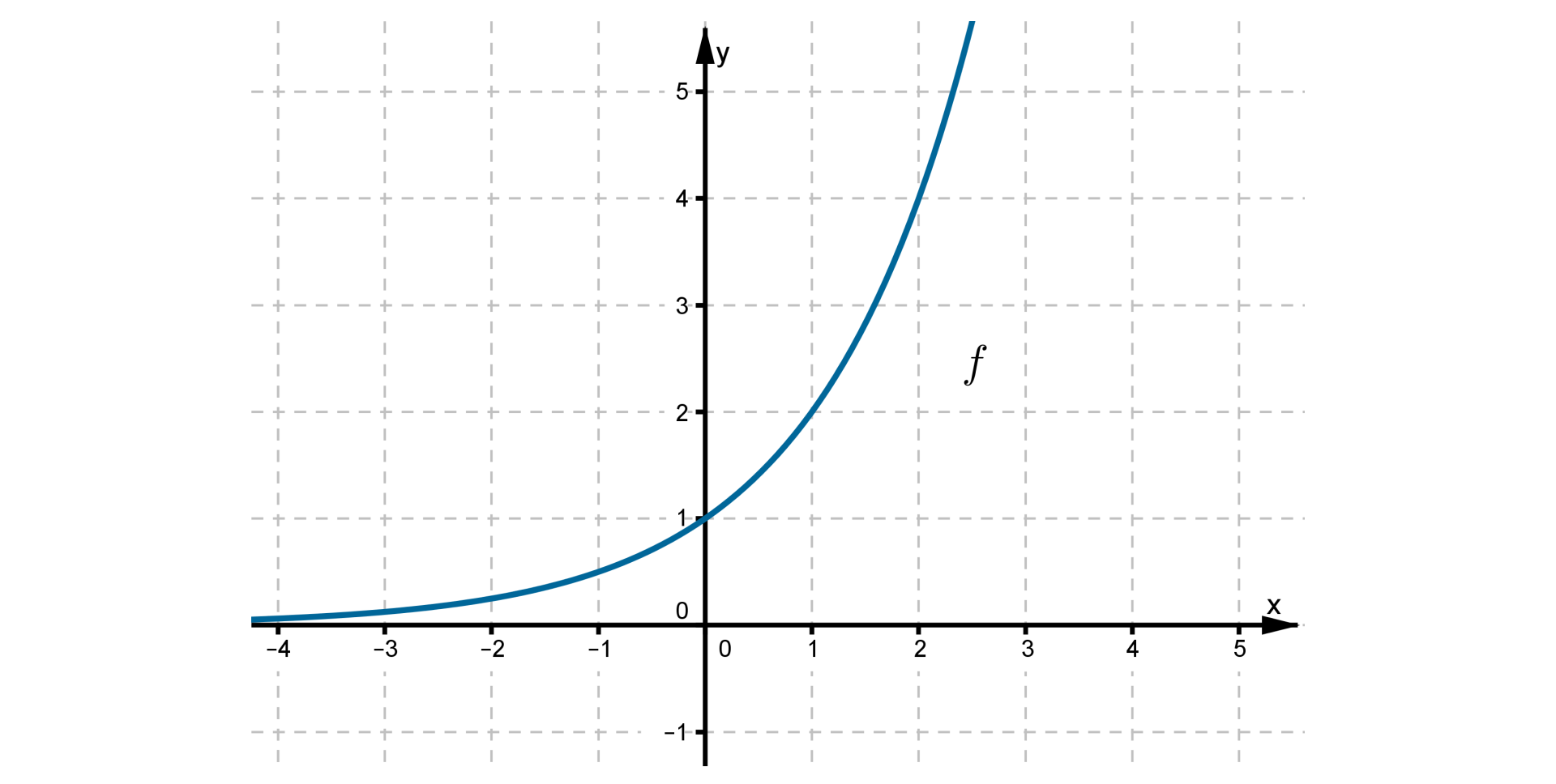
Jest to funkcja: Możliwe odpowiedzi: 1. rosnąca, 2. malejąca, 3. stała, 4. niemonotoniczna
Na rysunku przedstawiony jest wykres funkcji .

Jest to funkcja: Możliwe odpowiedzi: 1. rosnąca, 2. malejąca, 3. nierosnąca, 4. niemalejąca, 5. stała, 6. niemonotoniczna
Na rysunku przedstawiony jest wykres funkcji .

Jest to funkcja: Możliwe odpowiedzi: 1. rosnąca, 2. malejąca, 3. nierosnąca, 4. niemalejąca, 5. stała, 6. niemonotoniczna
Na rysunku przedstawiony jest wykres funkcji .

Jest to funkcja: Możliwe odpowiedzi: 1. rosnąca., 2. malejąca., 3. nierosnąca., 4. niemalejąca., 5. stała., 6. niemonotoniczna.
Na rysunku przedstawiony jest wykres funkcji .

Jest to funkcja: Możliwe odpowiedzi: 1. rosnąca, 2. malejąca, 3. nierosnąca, 4. niemalejąca, 5. stała, 6. niemonotoniczna
Na rysunku przedstawiony jest wykres funkcji .

Jest to funkcja: Możliwe odpowiedzi: 1. rosnąca., 2. malejąca., 3. nierosnąca., 4. niemalejąca., 5. stała., 6. niemonotoniczna.
Na rysunku przedstawiony jest wykres funkcji .
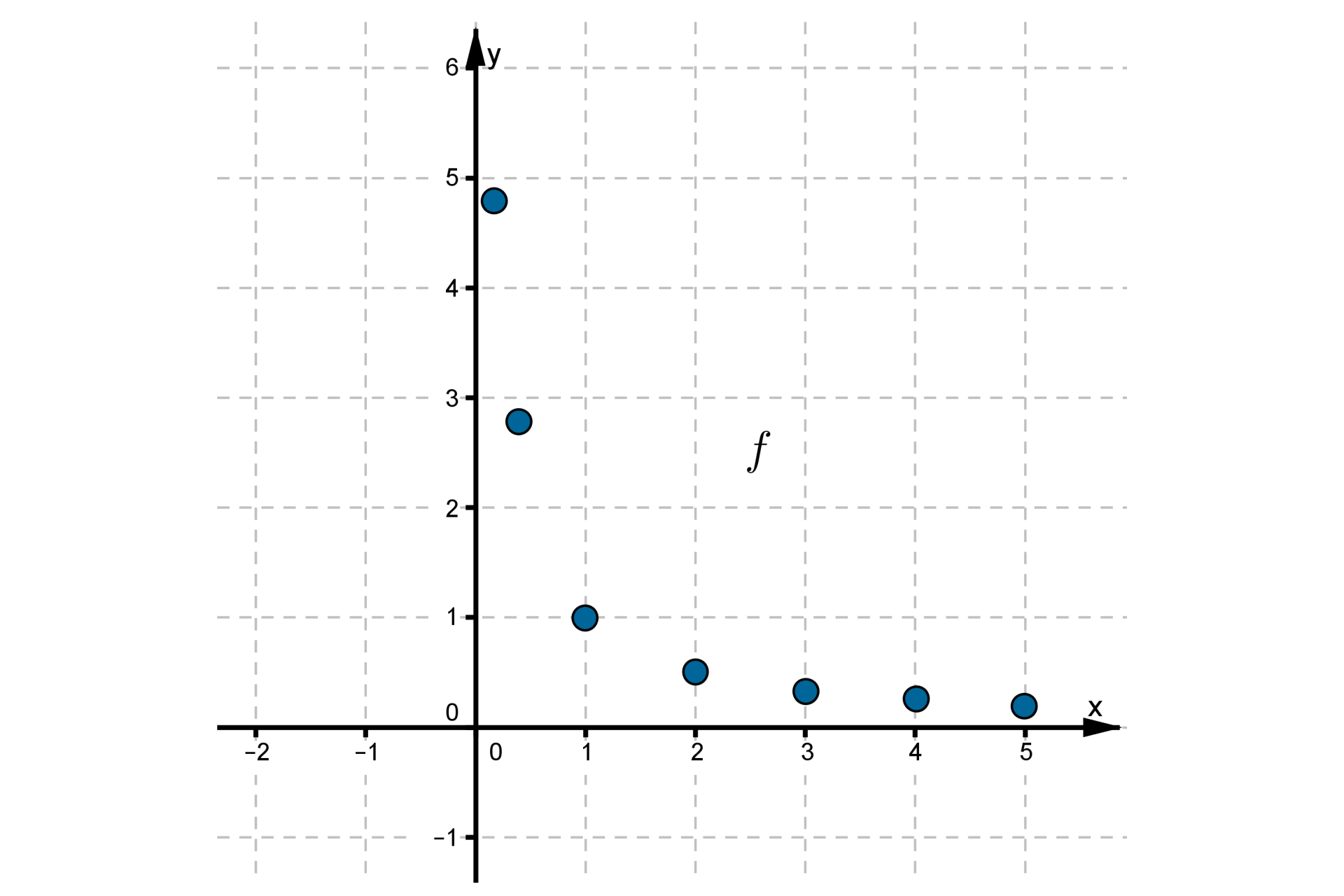
Jest to funkcja: Możliwe odpowiedzi: 1. rosnąca., 2. malejąca., 3. nierosnąca., 4. niemalejąca., 5. stała., 6. niemonotoniczna.
Na rysunku przedstawiony jest wykres funkcji .

Jest to funkcja: Możliwe odpowiedzi: 1. rosnąca, 2. malejąca, 3. nierosnąca, 4. niemalejąca, 5. stała, 6. niemonotoniczna
Na rysunku przedstawiony jest wykres funkcji .

Jest to funkcja: Możliwe odpowiedzi: 1. rosnąca, 2. malejąca, 3. nierosnąca, 4. niemalejąca, 5. stała, 6. niemonotoniczna
Na rysunku przedstawiony jest wykres funkcji .
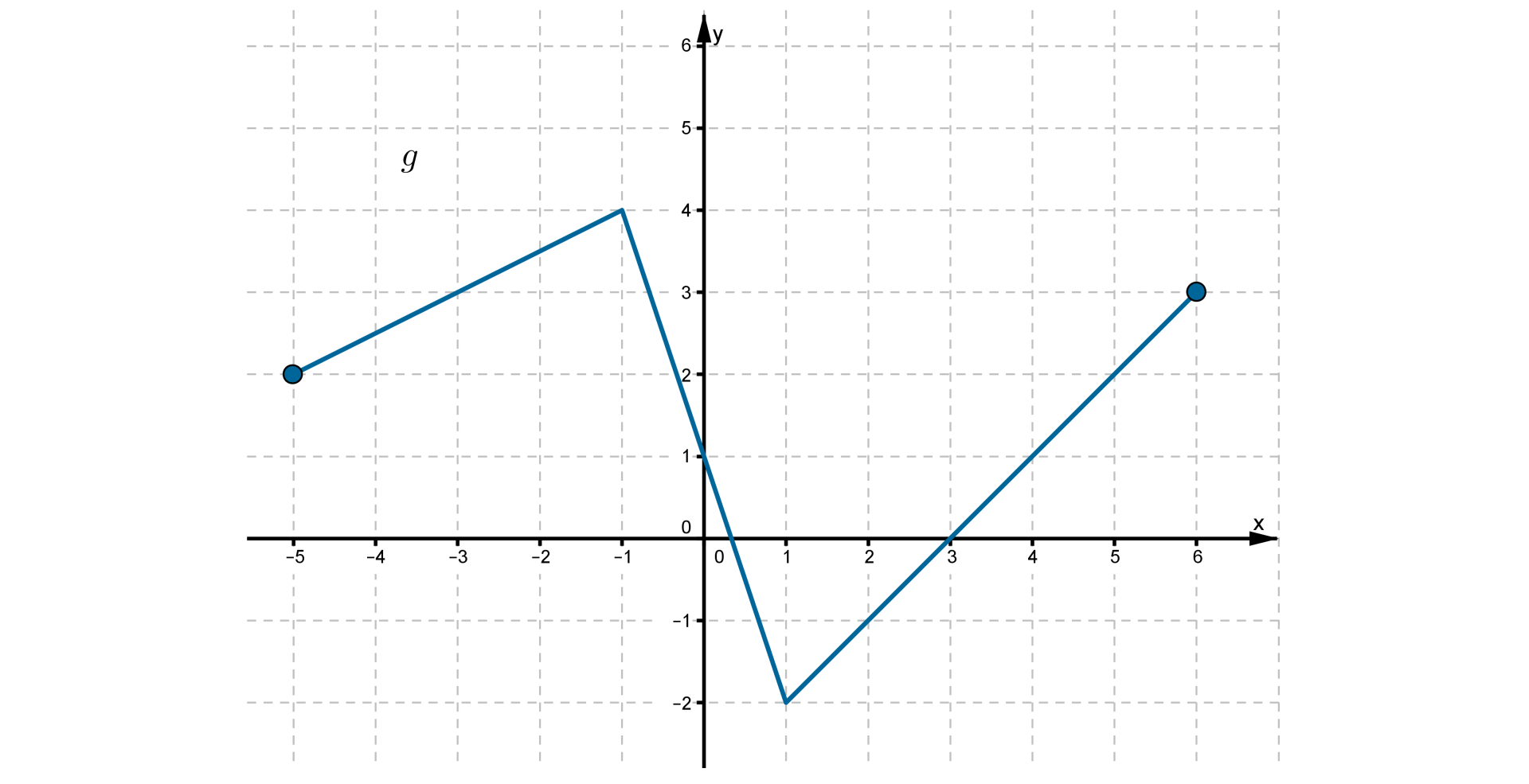
Funkcja jest rosnąca w przedziale: Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Na rysunku przedstawiony jest wykres funkcji .
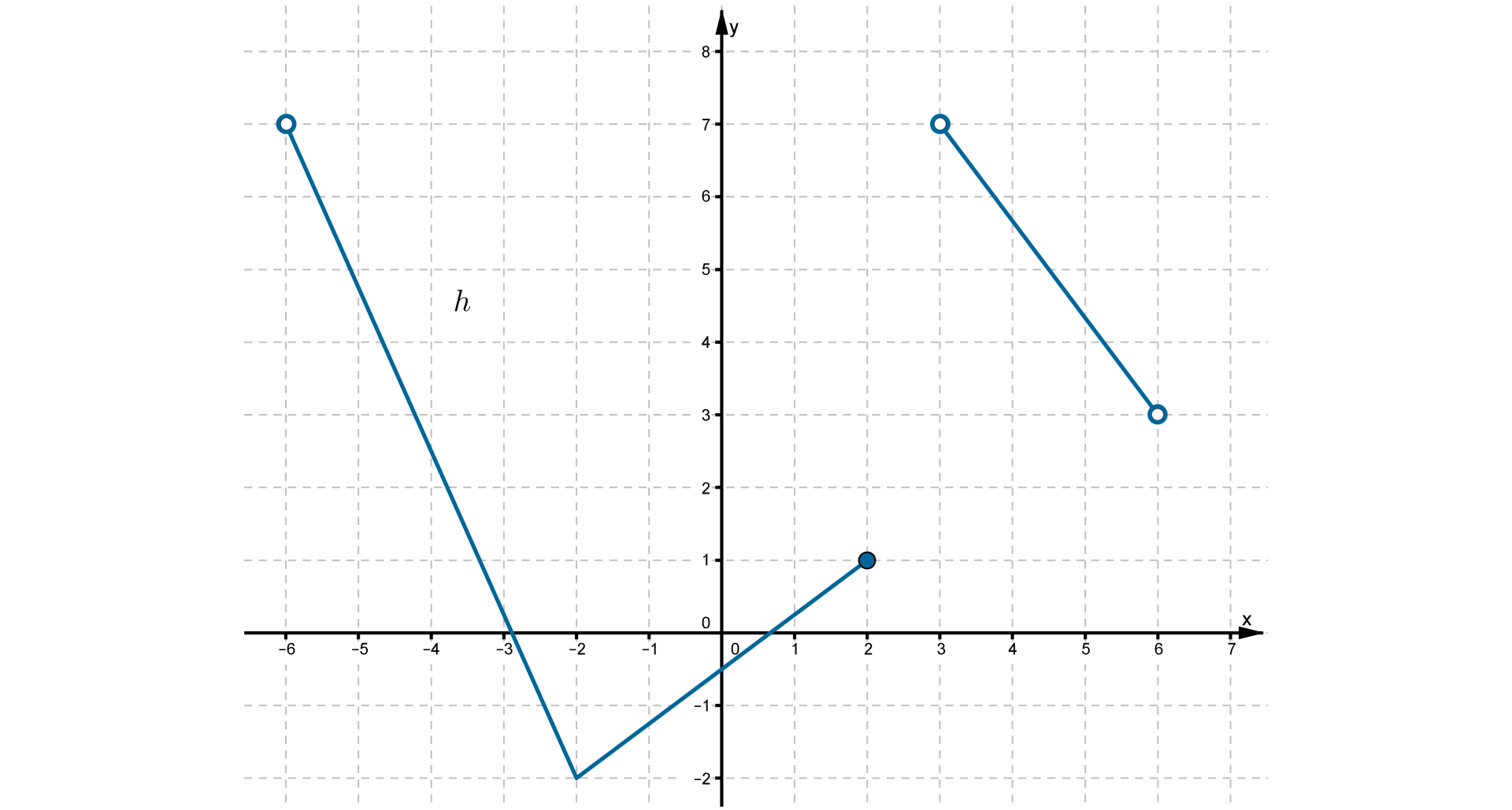
Funkcja jest malejąca w przedziale: Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Na rysunku przedstawiony jest wykres funkcji .

Maksymalnym przedziałem, w którym funkcja jest malejąca, jest przedział: Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Jakie funkcje przedstawiono na poniższych ilustracjach? Uzupełnij puste luki, wpisując jedno z określeń: malejąca, rosnąca, niemonotoniczna.