Punkty, proste i płaszczyzny w przestrzeni

Learning objectives

You will learn to identify mutual position of lines in space, especially perpendicular lines that do not cross and also to apply the concept of an angle between the line and the plane as well as the dihedral angle between half‑planes.

Learning effect

• You identify mutual position of lines in space, especially perpendicular lines that do not cross and also apply the concept of an angle between the line and the plane as well as the dihedral angle between half‑planes.

Prepare information about the following subjects:

1. Mutual position of the line and the planeplaneplane.

2. Mutual position of lines in space.

3. The angle between the line and the planeplaneplane.

4. The dihedral angledihedral angledihedral angle between half‑planes.

Check if information you prepared is the same as the following one:

1. Mutual position of the line and the planeplaneplane

• a line is located on the plane (each point of the line is also a point of the planeplaneplane),

• a line breaks the planeplaneplane (the line has exactly one common point with the planeplaneplane),

• a line is parallel to the planeplaneplane and has no common points with it.

2. Mutual position of lines in space

• Lines overlap (they are parallel),

• Lines are located on one planeplaneplane and cross at one point,

• Lines are located on one planeplaneplane and have no common points (they are parallel),

• Lines are not located on one planeplaneplane and have no common points (they are oblique).

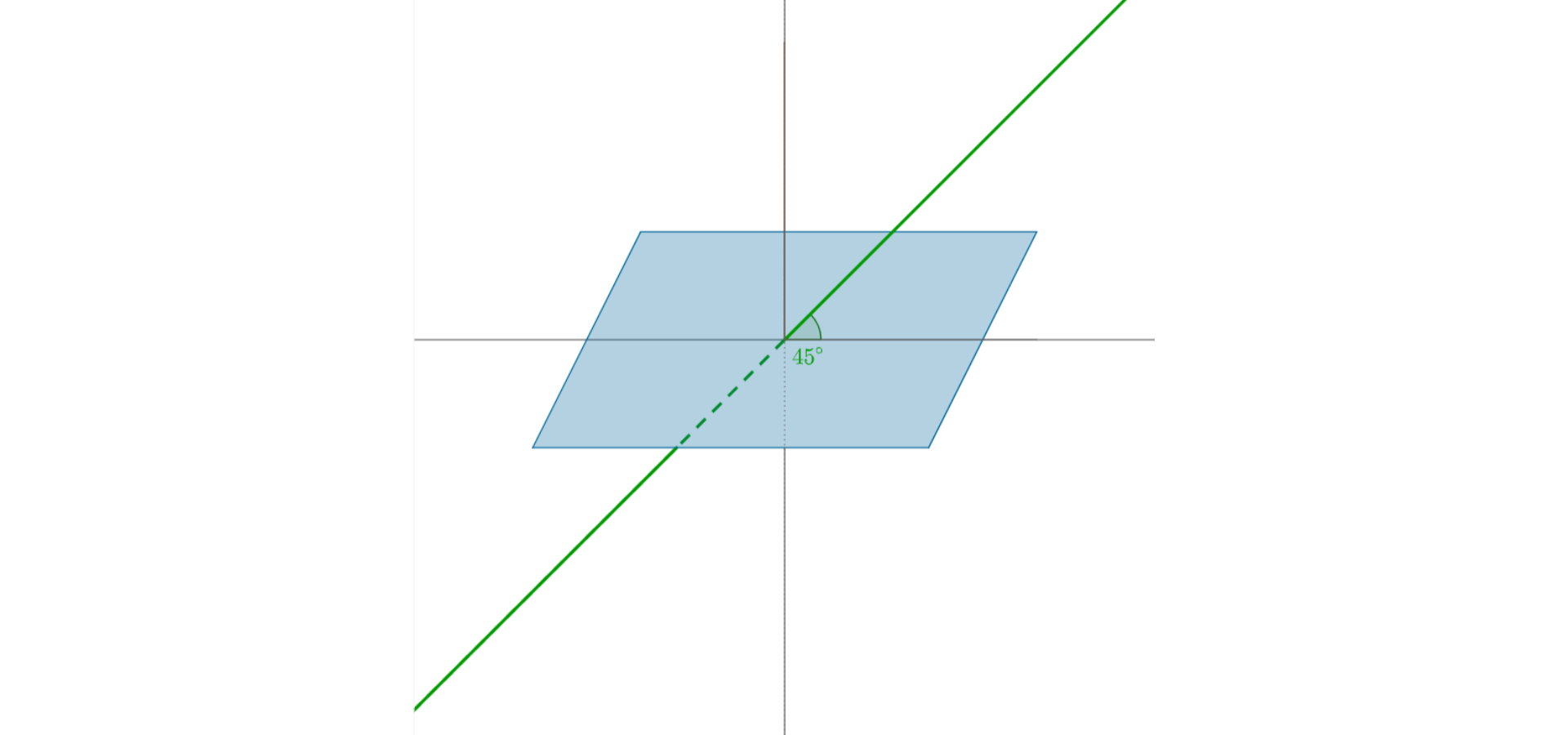
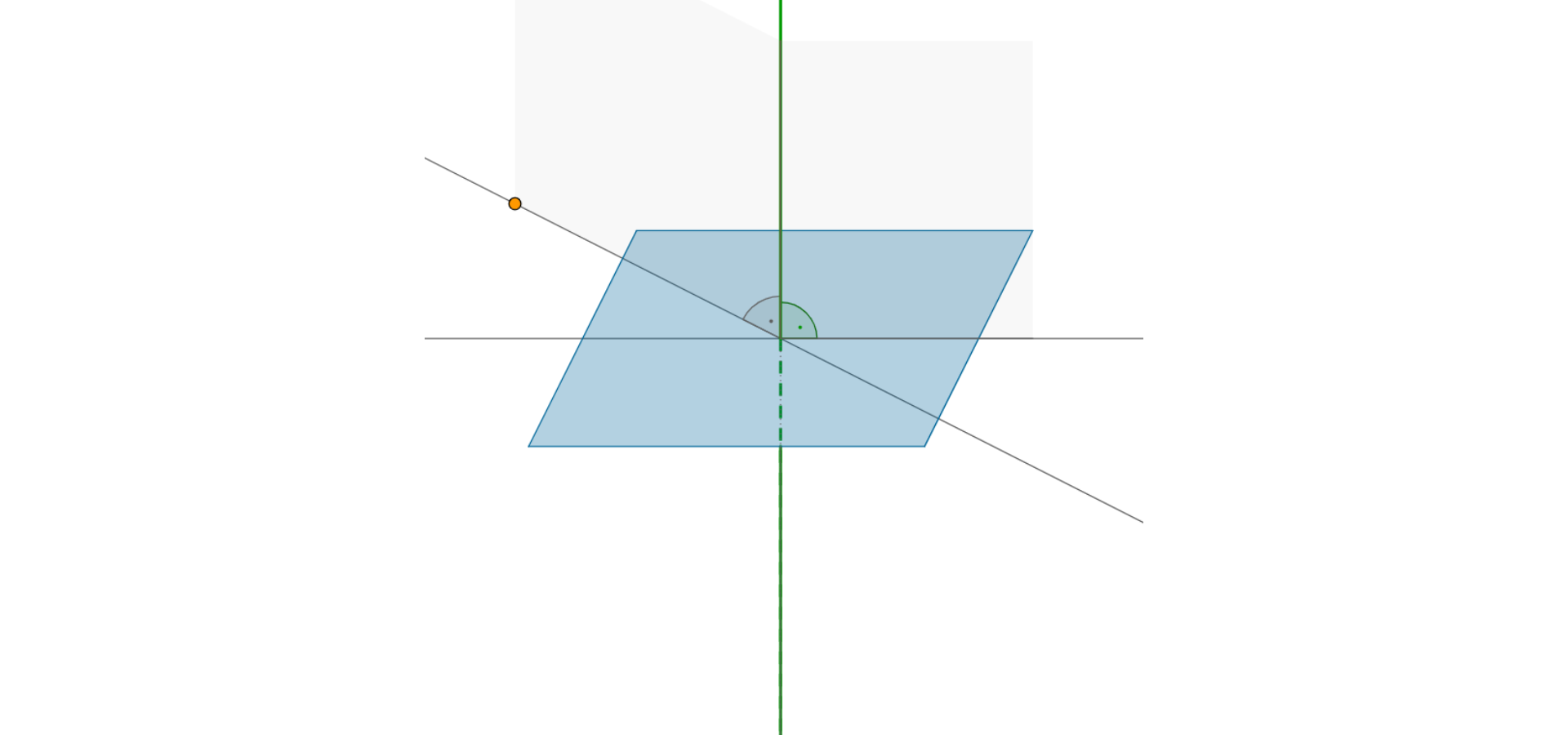
3. The angle between the line and the planeplaneplane

• The line k and the planeplaneplane p are perpendicular only and only if the line k is parallel to each line located on the planeplaneplane p,

• The angle between the line k and the plane pangle between the line k and the plane pangle between the line k and the plane p is the acute angle between this line and orthographic projection on the planeorthographic projection on the planeorthographic projection on the plane p,

• If the line l breaks the planeplaneplane p and is not perpendicular to it, the line k is an orthographic projection of the line l on the planeplaneplane p, the line m is located on the planeplaneplane p and crosses the line l, then the line m is perpendicular to the line l only and only if it is perpendicular to the line k (theorem about three perpendicular linesperpendicular linesperpendicular lines).

4. The dihedral angledihedral angledihedral angle between half‑planes

• the dihedral angledihedral angledihedral angle is the sum of two half‑planes with common edge and one of two areas that this half‑planes cut from the space,

• the linear anglelinear anglelinear angle of the dihedral angledihedral angledihedral angle is the common part of the dihedral angledihedral angledihedral angle and the planeplaneplane perpendicular to its edge.

Task 1

RhCWK6JhLNz2t1

nagranie abstraktu

nagranie abstraktu

Nagranie dostępne na portalu epodreczniki.pl

nagranie abstraktu

Open the applet and observe the angle that a line creates with a planeplaneplane. Compare animations with information you prepared.

R1KCGGhUumdC71

Aplet geogebra: Kąt między prostą a płaszczyzną. Poniżej znajduje się galeria będąca wersją alternatywną dla aplikacji.

Aplet geogebra: Kąt między prostą a płaszczyzną. Poniżej znajduje się galeria będąca wersją alternatywną dla aplikacji.

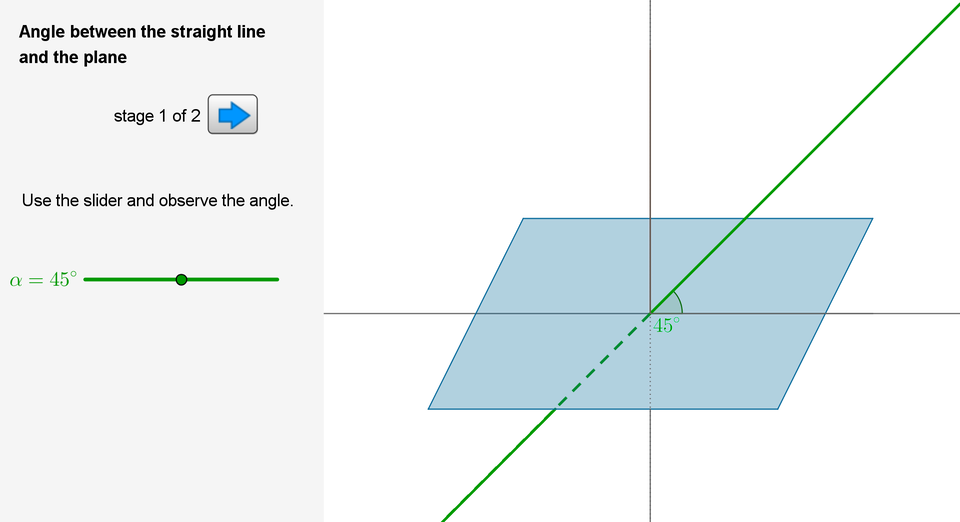
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dt3WttEZ6

R1ZXFTIL4cTj31

Na rysunku przedstawiona jest płaszczyzna oraz trzy proste. Jedna prosta leży na płaszczyźnie. Druga jest prostopadła do płaszczyzny. Trzecia przebija płaszczyznę w tym samym punkcie, co druga prosta i jest nachylona do płaszczyzny pod kątem 45°. Na rysunku zaznaczony jest również wyżej wymieniony kąt.

RbTzYYcIWKJ4r1

Na rysunku przedstawiona jest płaszczyzna oraz trzy proste. Dwie proste leżą na płaszczyźnie. Trzecia jest prostopadła do każdej z nich. Na rysunku zaznaczone są również wyżej wymienione kąty proste.

Do the revision exercises.

Remember:

• A line can be located on the planeplaneplane, break the planeplaneplane or have no common points with the planeplaneplane.

• Two lines in space can overlap, be located on one planeplaneplane or not be located on one planeplaneplane and have no common points (be oblique).

• The line k and the planeplaneplane p are perpendicular only and only if the line k is parallel to each line located on the planeplaneplane p.

• The angle between the line k and the plane pangle between the line k and the plane pangle between the line k and the plane p is the acute angle between this line and orthographic projection on the planeorthographic projection on the planeorthographic projection on the plane p.

• If the line l breaks the planeplaneplane p and is not perpendicular to it, the line k is an orthographic projection of the line l on the planeplaneplane p, the line m is located on the planeplaneplane p and crosses the line l, then the line m is perpendicular to the line l only and only if it is perpendicular to the line k (theorem about three perpendicular linesperpendicular linesperpendicular lines).

• The dihedral angledihedral angledihedral angle is the sum of two half‑planes with common edge and one of two areas that this half‑planes cut from the space.

• The linear anglelinear anglelinear angle of the dihedral angledihedral angledihedral angle is the common part of the dihedral angledihedral angledihedral angle and the planeplaneplane perpendicular to its edge.

Exercises

Glossary

Keywords

angle between the line k and the plane pangle between the line k and the plane pangle between the line k and the plane p - kąt ostry między tą prostą i jej rzutem prostokątnym l na płaszczyznę p

dihedral angledihedral angledihedral angle - suma dwóch półpłaszczyzn o wspólnej krawędzi i jednego z dwóch obszarów, które te półpłaszczyzny wycinają z przestrzeni

line that breaks the planeline that breaks the planeline that breaks the plane

oblique linesoblique linesoblique lines

orthographic projection on the planeorthographic projection on the planeorthographic projection on the plane