Pola figur podobnych
Stosunek pól figur podobnych
Wiemy, że stosunek odpowiednich odcinków figur podobnych jest równy skali podobieństwa.
Zastanowimy się teraz, jaka jest zależność między polami takich figur.
Przyjmijmy, że pole niebieskiego kwadratu jest równe . Kwadrat ten jest podobny do każdego z pozostałych kwadratów. Pod rysunkami zapisana jest skala podobieństwa danego kwadratu do kwadratu niebieskiego. Zapisane są też pola tych figur. Co zauważasz?

Odpowiedź. Pole kwadratu jest równe kwadratowi skali podobieństwa.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D14ATWBkl
Przyprostokątne trójkąta prostokątnego mają długości i . Każdą z przyprostokątnych zmniejszamy dwukrotnie. Oblicz stosunek pola pomniejszonego trójkąta do pola danego trójkąta.
Każdy z boków trójkąta zmniejszono dwukrotnie. Zatem skala podobieństwa trójkąta otrzymanego do trójkąta danego jest równa . Wynika z tego, że przyprostokątne trójkąta pomniejszonego mają długości i .
Oznaczmy:
– pole danego trójkąta,
– pole trójkąta pomniejszonego.
Stosunek pól tych trójkątów jest równy , czyli jest równy kwadratowi skali podobieństwa.
Prostokątna kartka w notesie ma wymiary i . Kartka w książce ma wymiary i . Ile razy pole powierzchni kartki w książce jest większe od pola powierzchni kartki w notesie?
Zauważmy, że prostokąty, w kształcie których są kartki, są podobne. Skala podobieństwa prostokąta w kształcie którego jest kartka w książce do prostokąta, w kształcie którego jest kartka w notesie, jest równa
Obliczamy stosunek pól tych prostokątów.
Stosunek pól powierzchni kartek jest równy , czyli jest równy kwadratowi skali podobieństwa.
Na podstawie powyższych przykładów możemy wnioskować, że jeśli figura jest podobna do figury w skali , to stosunek pól tych figur jest równy .
Sprawdźmy nasze przypuszczenia jeszcze na kilku przykładach.
Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa.
Pięciokąt jest podobny do pięciokąta w skali . Pole pięciokąta jest równe . Oblicz pole pięciokąta .
Korzystamy z tego, że stosunek pól wielokątów podobnych jest równy kwadratowi skali podobieństwa. Stąd
Pole pięciokąta jest równe .
Jedną z największych atrakcji turystycznych Gdańska jest Bazylika Mariacka, na której znajduje się największy w Polsce zegar. Został on zbudowany w .
Pole powierzchni tarczy tego zegara jest równe około . Pole powierzchni tarczy zegarka na rękę jest równa około . Określ skalę podobieństwa tych tarcz.
Zapisujemy oba pola w tej samej jednostce pola.
Dzielimy pole powierzchni większej tarczy przez pole powierzchni mniejszej tarczy. Obliczamy w ten sposób kwadrat skali podobieństwa tarcz.
Obliczamy teraz skalę podobieństwa.
Skala podobieństwa tarczy gdańskiego zegara do tarczy zegarka na rękę wynosi .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D14ATWBkl
Obliczanie pól figur podobnych
Zauważmy, że jeżeli figura jest podobna do figury w skali , pole figury jest równe , a pole figury jest równe , to oraz . Wykorzystamy teraz podane równości w zadaniach.
Figury i są podobne. Pole figury jest równe . Oblicz pole figury .
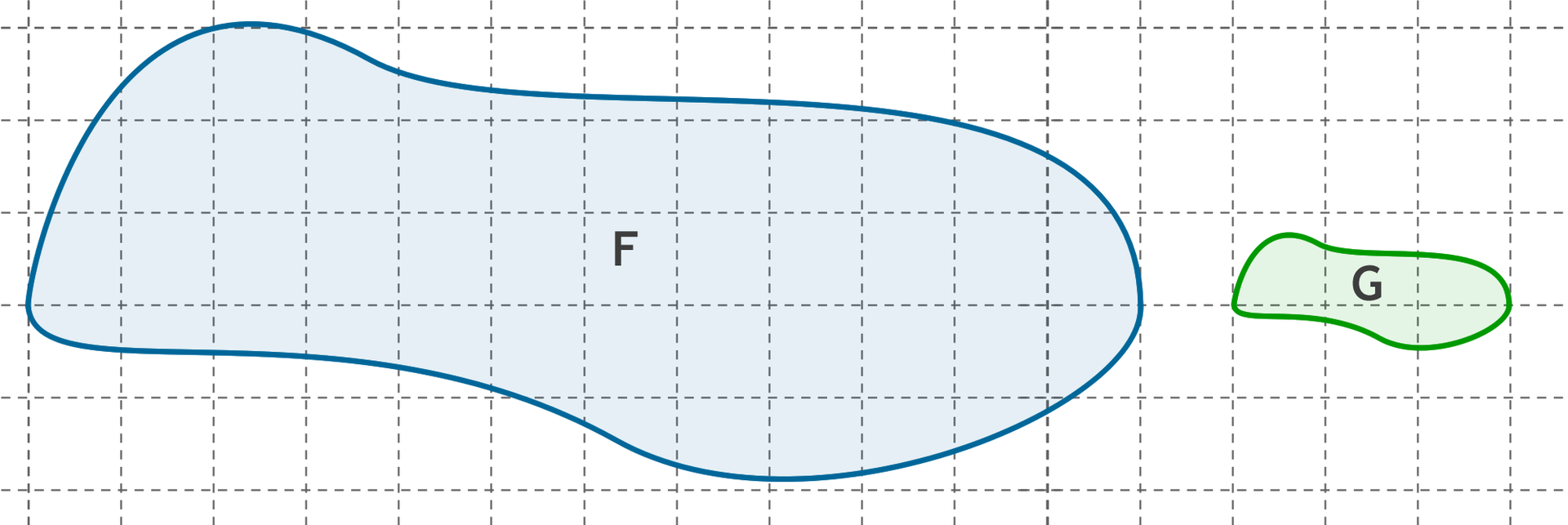
Określamy najpierw skalę podobieństwa figur. W tym celu zaznaczamy w obu figurach odpowiadające sobie odcinki. Skala podobieństwa figury do figury jest równa stosunkowi długości tych odcinków.
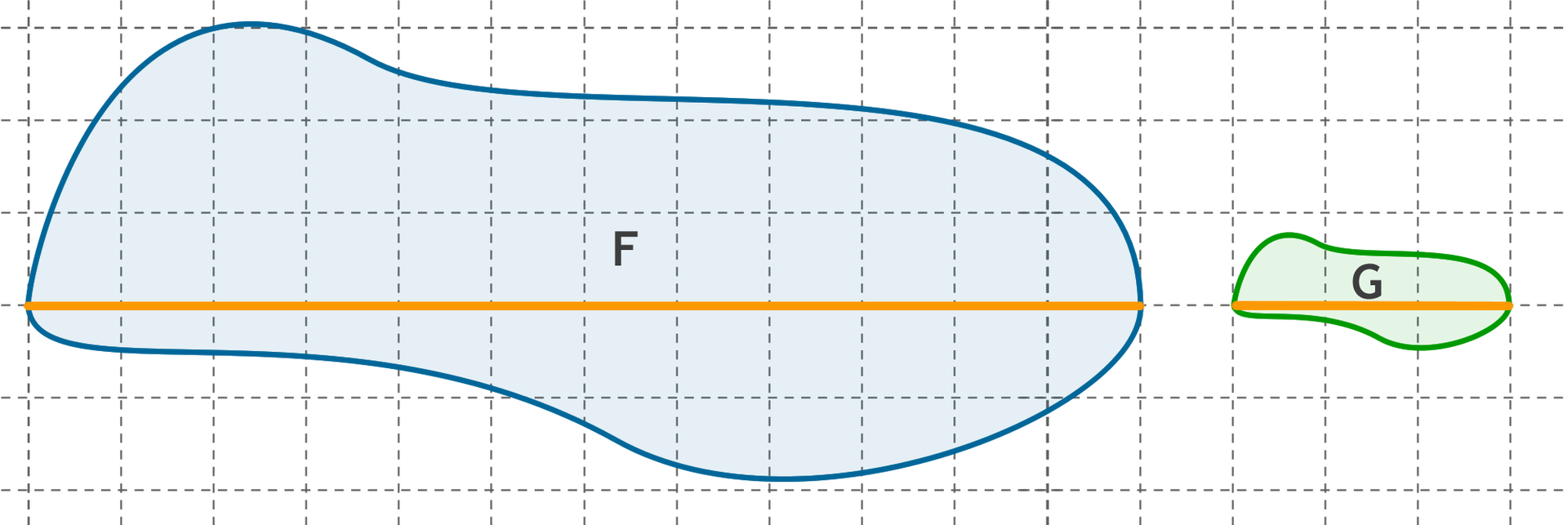
Jeżeli przyjmiemy, że długość małej kratki jest równa , to
Zatem , gdzie
– pole figury
– pole figury
Stąd
Pole figury jest równe .
Pole rombu jest równe . Romb ten jest podobny do rombu , którego przekątne mają długości i . Znajdź sumę długości przekątnych rombu .
Oznaczmy:
– pole rombu ,
- pole rombu ,
- skala podobieństwa rombu do rombu .
Wtedy
bo
Skala podobieństwa rombów jest równa . Oznacza to, że każda z przekątnych rombu jest razy dłuższa od odpowiedniej przekątnej rombu .
Zatem długości przekątnych rombu są równe i .
Suma długości tych przekątnych jest równa .
Dwa wielokąty są podobne. Obwód pierwszego z nich jest równy , a pole . Obwód drugiego wielokąta jest równy . Oblicz pole drugiego wielokąta.
Obliczamy skalę podobieństwa wielokątów.
Obliczamy pole drugiego wielokąta.
Pole drugiego wielokąta jest równe .
Skala podobieństwa dwóch kwadratów jest równa . Oblicz długość boku mniejszego kwadratu, jeżeli różnica pól tych kwadratów wynosi .
Niech P oznacza pole mniejszego kwadratu. Wtedy pole większego kwadratu to
Zatem
Korzystamy z tego, że różnica pól tych kwadratów jest równa i wyznaczamy pole mniejszego kwadratu i długość a jego boku.
bo
Długość boku mniejszego kwadratu jest równa .
Podstawy trapezu równoramiennego mają długości i . Przekątne trapezu przecinają się w punkcie . Wysokość trójkąta jest równa . Oblicz pole trapezu.

Zauważmy, że trójkąty i mają równe kąty: kąty i to kąty wierzchołkowe, mają więc równe miary, kąty i to kąty naprzemianległe przy prostych równoległych, podobnie kąty i . Na podstawie cechy stwierdzamy, że trójkąty i są podobne.
Skala podobieństwa tych trójkątów jest równa stosunkowi długości ich podstaw.
Stosunek wysokości tych trójkątów jest równy skali podobieństwa.
Wysokość trapezu jest równa sumie wysokości trójkątów i .
Obliczamy pole trapezu.
Pole trapezu jest równe .
Jezioro Śniardwy to największe jezioro w Polsce. Powierzchnia tego jeziora jest równa około . Na mapie powierzchnia ta jest równa . W jakiej skali wykonana jest mapa?
Zapisujemy najpierw powierzchnię jeziora w cmIndeks górny 22.
Obliczamy kwadrat skali podobieństwa figury, w kształcie której jest jezioro na mapie, i figury, w kształcie której jest powierzchnia jeziora w rzeczywistości.
Obliczamy skalę podobieństwa tych figur.
Skala mapy jest równa obliczonej skali podobieństwa.
Mapa wykonana jest więc w skali .
Figura jest podobna do figury w skali . Stosunek pola figury do pola figury jest równy
Wiadomo, że , , . Trójkąt jest podobny do trójkąta w skali .
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Pole trójkąta jest dwukrotnie mniejsze od pola trójkąta .
- Pole trójkąta jest dwukrotnie mniejsze od pola trójkąta .
- Suma pola trójkąta ABC i pola trójkąta jest równa .
- Różnica pola trójkąta i pola trójkąta jest mniejsza od .
Pole koła zwiększono stukrotnie. Wynika z tego, że
- promień koła zwiększono stukrotnie
- obwód koła zwiększono dziesięciokrotnie
- średnicę koła zwiększono dwudziestokrotnie
Pole powierzchni kwadratowej działki pani jest razy większe od pola kwadratowej działki pani . Ile razy więcej siatki trzeba kupić na odgrodzenie działki pani niż działki pani ?
Stosunek obwodów dwóch kół jest równy . Stosunek pola większego koła do mniejszego jest równy
Płytka terakoty jest w kształcie sześciokąta foremnego. Płytka glazury ma również kształt sześciokąta foremnego.

W sześciokątach tych dłuższe przekątne są odpowiednio równe i . Ile razy większe jest pole powierzchni płytki terakoty od pola powierzchni płytki glazury?
Trapez jest podobny do trapezu w skali . Wynika stąd, że
obwód trapezu jest razy większy od obwodu trapezu
wysokość trapezu stanowi wysokości trapezu
pole trapezu stanowi pola trapezu
pole trapezu jest o większe od pola trapezu
Ile spośród podanych stwierdzeń jest prawdziwych?
- jedno
- żadne
- wszystkie
- trzy
Trójkąt o bokach długości , , jest podobny do trójkąta . Pole trójkąta jest równe . Oblicz długości boków trójkąta .
Przekątne rombu są równe i . Pole rombu W jest równe . Dłuższa przekątna rombu jest równa
Prostokąt jest podobny w skali do prostokąta , którego pole wynosi . Oblicz pole prostokąta dla:
Równoległobok jest podobny do równoległoboku w skali . Jaki jest stosunek pól tych równoległoboków?
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Dowolne dwa czworokąty o równych polach są podobne.
- Dowolne dwa wielokąty podobne mają jednakowe pola.
- Dowolne dwa sześciokąty foremne o jednakowych polach są podobne.
W trójkącie prostokątnym wysokość poprowadzona z wierzchołka kąta prostego podzieliła przeciwprostokątną długości na dwa odcinki , z których jeden ma długość . Oblicz pole trójkąta.
Prostokątną fotografię o wymiarach na powiększono na kserografie tak, że jej szerokość jest równa . Jakie pole ma powiększona fotografia?
Wycinek koła o promieniu ma pole równe . Wycinek koła o promieniu ma pole równe . Czy wycinki te są podobne? Jeśli tak, podaj ich skalę podobieństwa.
Koło jest podobne do koła w skali . Oblicz pole koła , jeśli wiadomo, że wycinkowi koła o polu odpowiada kąt środkowy o mierze .
Dwa sześciokąty foremne mają pola równe oraz . Oblicz długości boków tych sześciokątów oraz określ skalę podobieństwa promieni okręgów wpisanych w te sześciokąty.
Podstawami trapezu są odcinki i . Przekątne tego trapezu przecinają się w punkcie . Pole trójkąta jest równe , pole trójkąta jest równe . Oblicz pole trapezu.