Jeśli w samochodzie przepali się jeden z reflektorów, to czy pozostałe światła będą działać bez zarzutu? Jeśli chcesz poznać odpowiedź na to pytanie, czytaj dalej.

REZqXZXGoCFiM1

Zdjęcie przedstawia sufit w eleganckiej sali biurowej lub prezentacyjnej. Widoczne liczne lampki zapewniające tak zwane oświetlenie punktowe umieszczone zarówno na suficie, jak i podwieszanych pod nim elementach dekoracyjnych. Łącznie około trzydziestu punktów świetlnych białych i niebieskawych. — System połączeń równoległych stosuje się m.in. w układach oświetleniowych. Ma on liczne zalety, m.in. zapewnia każdej lampie takie samo napięcie niezależnie od ich liczby, a awaria jednej żarówki nie powoduje przerwania obwodu

Już potrafisz

podać definicję napięcia elektrycznego i jego jednostki – wolta (V);
podać definicję natężenia prądu elektrycznego i jego jednostki – ampera (A);
stwierdzić, że natężenie prądu płynącego przez przewodnik jest wprost proporcjonalne do napięcia przyłożonego między jego końcami;
zdefiniować opór elektryczny przewodnika jako stosunek napięcia przyłożonego między jego końcami do natężenia prądu, który tamtędy płynie;
podać definicję jednostki oporu elektrycznego – oma (Ω).

Nauczysz się

rozpoznawać połączenie równoległe odbiorników (na schematach i w praktyce);
posługiwać się zależnościami między natężeniem, napięciem a oporem elektrycznym w połączeniu równoległym odbiorników;
rozwiązywać problemy i zadania dotyczące połączenia równoległego odbiorników prądu elektrycznego.

ime5s9ZIxT_d5e304

1. Połączenie równoległe – podstawy teoretyczne

Natężenie prądu płynącego przez przewodnik podłączony do stałego źródła napięcia ma jednakową wartość w każdym miejscu przewodnika. Co się jednak stanie, jeśli nastąpi rozgałęzienie przewodnika, czyli gdy będzie on doprowadzał prąd do urządzeń połączonych równolegle? Czy natężenie prądu również będzie miało identyczną wartość?

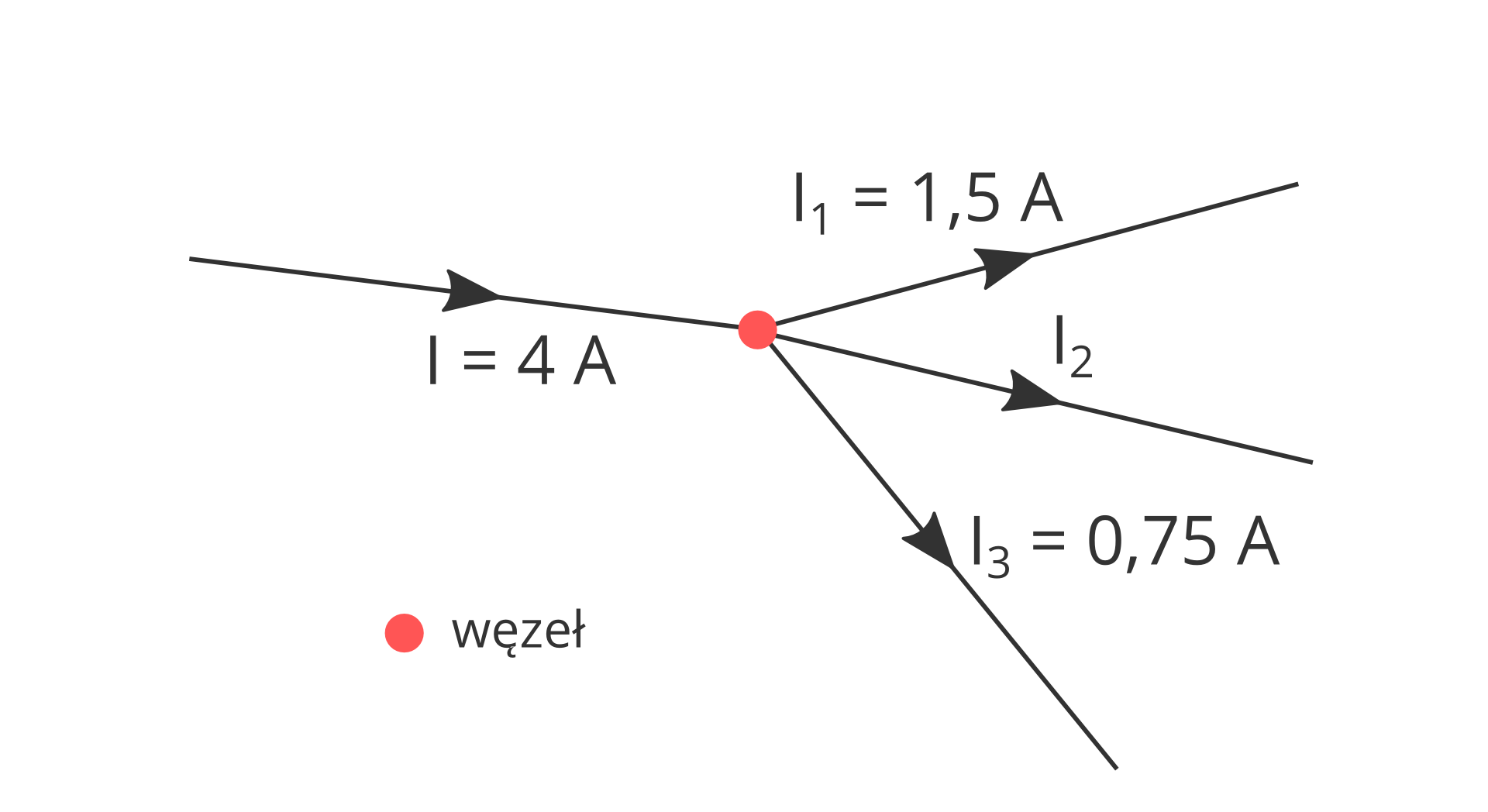
Punkt, w którym następuje rozgałęzienie, nazywany jest węzłem. Przepływ prądu oznacza, że do węzła dopływa jakiś ładunek w jednostce czasu. Natężenie prądu dopływającego do węzła jest równe $I$ , a ładunek $q = I \cdot t$ . Z węzła wychodzą dwa przewody, w których natężenia prądu są różne. Oznaczmy je $I_{1}$ oraz $I_{2}$ , przy czym ładunki wypływające w jednostce czasu z węzła muszą w sumie być równe ładunkowi q wpływającemu do węzła (zasada zachowania ładunku). Wynika z tego, że suma natężeń prądów wypływających z węzła jest równa natężeniu prądu dopływającego do tego węzła, czyli:

I = I_{1} + I_{2}

R945xqDXEKHCu1

Tę zależność nazywamy pierwszym prawem KirchhoffaGustaw Robert KirchhoffKirchhoffa.

pierwsze prawo Kirchhoffa

Prawo: pierwsze prawo Kirchhoffa

Suma natężeń prądów wpływających do dowolnego węzła jest równa sumie natężeń prądów wypływających z tego węzła.

Jeśli odbiorniki są połączone równoległe, oznacza to, że są one połączone za pomocą przewodów z dwóch stron, a napięcie jest przyłożone do pary połączonych końcówek. Oznacza to, że napięcie zmierzone między końcami oporników jest jednakowe i równe napięciu elektrycznemu źródła. To samo dotyczy natężenia prądu – w obu przypadkach.

Oporniki połączone równolegle można zastąpić jednym równoważnym opornikiem, do którego końców przyłożone zostanie napięcie $U$ i przez który będzie przepływał prąd o natężeniu $I$ . Do końców tego opornika musi też zostać przyłożone napięcie $U$ . Natężenie tego prądu będzie równe sumie natężeń prądów w opornikach połączonych równolegle.
Aby wyznaczyć wartość oporu zastępczego, posłużymy się schematem i poznanymi zależnościami między napięciem, natężeniem a oporem elektrycznym.

R1BMW5H3OKUMa1

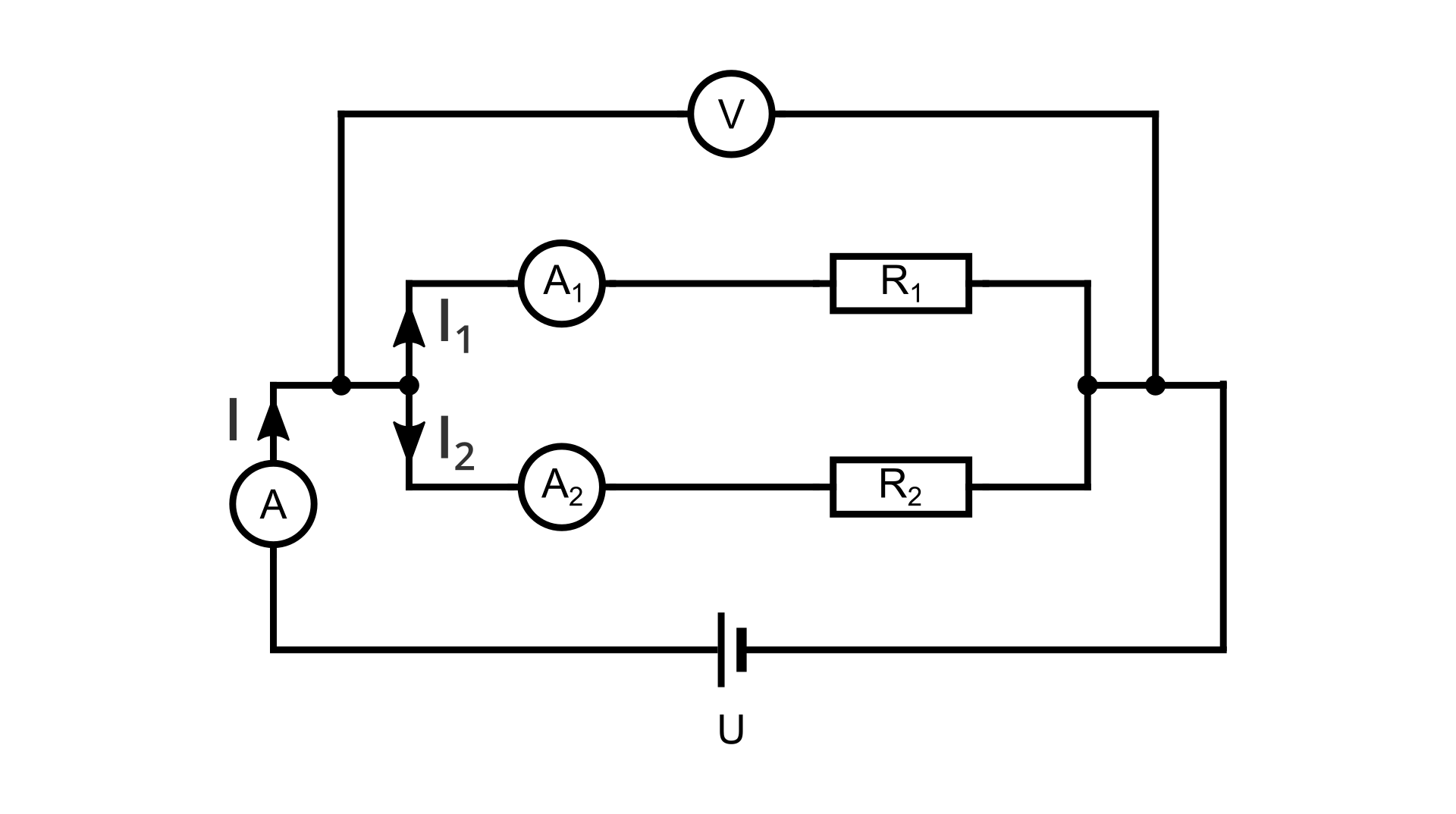
Połączenie równoległe oporników — Wyznaczanie wartości oporu zastępczego odbiorników prądu elektrycznego

Korzystamy z pierwszego prawa Kirchhoffa:
(1) $I = I_{1} + I_{2}$
Uwzględniamy zależność między napięciem ( $U$ ) a natężeniem ( $I$ ) i otrzymujemy:
(2) $U = I \cdot R$

Przekształcamy wzór (2), aby wyznaczyć natężenie:

(3) $I = \frac{U}{R}$
Do równania (1) podstawiamy zależność (3):

(4) $\frac{U}{R} = \frac{U}{R_{1}} + \frac{U}{R_{2}}$

Równanie (4) dzielimy przez napięcie ( $U$ ):

(5) $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$

Ze wzoru (5) wynika, że suma odwrotności oporów poszczególnych elementów jest równa odwrotności oporu zastępczego.

Przykład 1

Dwa oporniki o oporach $R_{1} = 2 Ω$ i $R_{2} = 3 Ω$ połączono równolegle. Oblicz opór zastępczy tych oporników.
Zależność:
$\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$
Dane:
$R_{1} = 2 Ω$
$R_{2} = 3 Ω$
Szukane:
$R = ?$
Obliczenia:
$\frac{1}{R} = \frac{1}{2 Ω} + \frac{1}{3 Ω}$
Ułamki sprowadzamy do wspólnego mianownika:
$\frac{1}{R} = \frac{3}{6 Ω} + \frac{2}{6 Ω}$
$\frac{1}{R} = \frac{5}{6 Ω}$
Aby obliczyć opór zastępczy, należy skorzystać z proporcji:
$5 \cdot R = 1 \cdot 6 Ω$ $/ : 5$
$R = 1,2 Ω$
Odpowiedź:
Opór zastępczy układu oporników wynosi $1,2 Ω$ .

R1Mirxjn7joJS1

Prawo Kirchhoffa-zadanie — Źródło: Krzysztof Jaworski, licencja: CC BY 3.0.

Ćwiczenie 1.1

R12SOXiocSoQV1

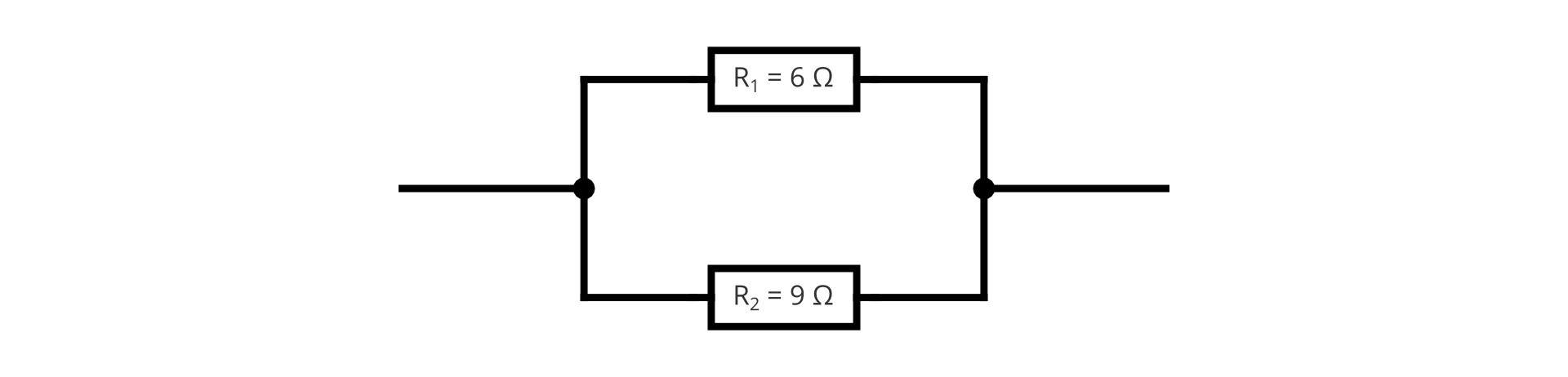
Korzystając z powyższego schematu obwodu elektrycznego, oblicz natężenie $I_{2}$ i wskaż prawidłową odpowiedź.

1,75 A
3,25 A
4,75 A
6,25 A

Źródło: Magdalena Grygiel <Magdalena.Grygiel@up.wroc.pl>, licencja: CC BY 3.0.

R1MJGOzM3ffUj1

Połączenie równoległe – opór zastępczy — Źródło: Krzysztof Jaworski, licencja: CC BY 3.0.

Ćwiczenie 2.1

R1MekDG12Zng41

Korzystając z powyższego schematu obwodu elektrycznego, oblicz opór zastępczy i wskaż prawidłową odpowiedź.

3,6 Ω
0,28 Ω
7,5 Ω
15 Ω

Źródło: Magdalena Grygiel <Magdalena.Grygiel@up.wroc.pl>, licencja: CC BY 3.0.

opornik zastępczy

– opornik zastępujący oporniki połączone równolegle. Do końców opornika zastępczego przyłożone jest napięcie $U$ ; płynie przez niego prąd o natężeniu $I$ będący sumą natężeń prądów w opornikach połączonych równolegle. Opór zastępczy w połączeniu równoległym oblicza się za pomocą wzoru:

\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \dots

gdzie:
$R_{n}$ opór $n$ -tego opornika; $R$ – opór zastępczy.

ime5s9ZIxT_d5e600

2. Połączenie równoległe – rozwiązywanie zadań

Przykład 2

Dwa oporniki o oporach $R_{1} = 20 Ω$ i $R_{2} = 30 Ω$ połączono równolegle. Oblicz natężenie prądu płynącego przez każdy opornik, jeśli podłączono je do źródła stałego napięcia równego $6 V$ .
Wzór:
$I = \frac{U}{R}$
Dane:
$R_{1} = 20 Ω$
$R_{2} = 30 Ω$
$U = 6 V$
Szukane:
$I_{1} = ?$
$I_{2} = ?$
Obliczenia:
$I_{1} = \frac{6 V}{20 Ω} = 0,3 A$

$I_{2} = \frac{6 V}{30 Ω} = 0,2 A$
Odpowiedź:
Przez opornik $R_{1}$ płynął prąd o natężeniu $0,3 A$ , a przez opornik $R_{2}$ – prąd o natężeniu $0,2 A$ .

Ćwiczenie 3

RpGFTIIXJPPic1

Dwa oporniki o oporach $R_{1} = 120 Ω$ i $R_{2} = 480 Ω$ połączono równolegle i przyłożono napięcie $U = 24 V$ . Oblicz natężenie prądu płynącego przez każdy opornik. Uzupełnij puste miejsca.

Zależności:
$I = \frac{U}{R}$

Dane:
$R_{1} =$ ............ Ω
$R_{2} =$ ............ Ω
$U =$ ............

Szukane:
$I_{1} =$ ?
$I_{2} =$ ?

Obliczenia:
$I_{1} =$ ............ : ............ Ω = ............

$I_{2} =$ ............ : ............ Ω = ............

Odpowiedź:
Natężenia prądu są równe ............ i .............

Źródło: Magdalena Grygiel <Magdalena.Grygiel@up.wroc.pl>, licencja: CC BY 3.0.

Przykład 3

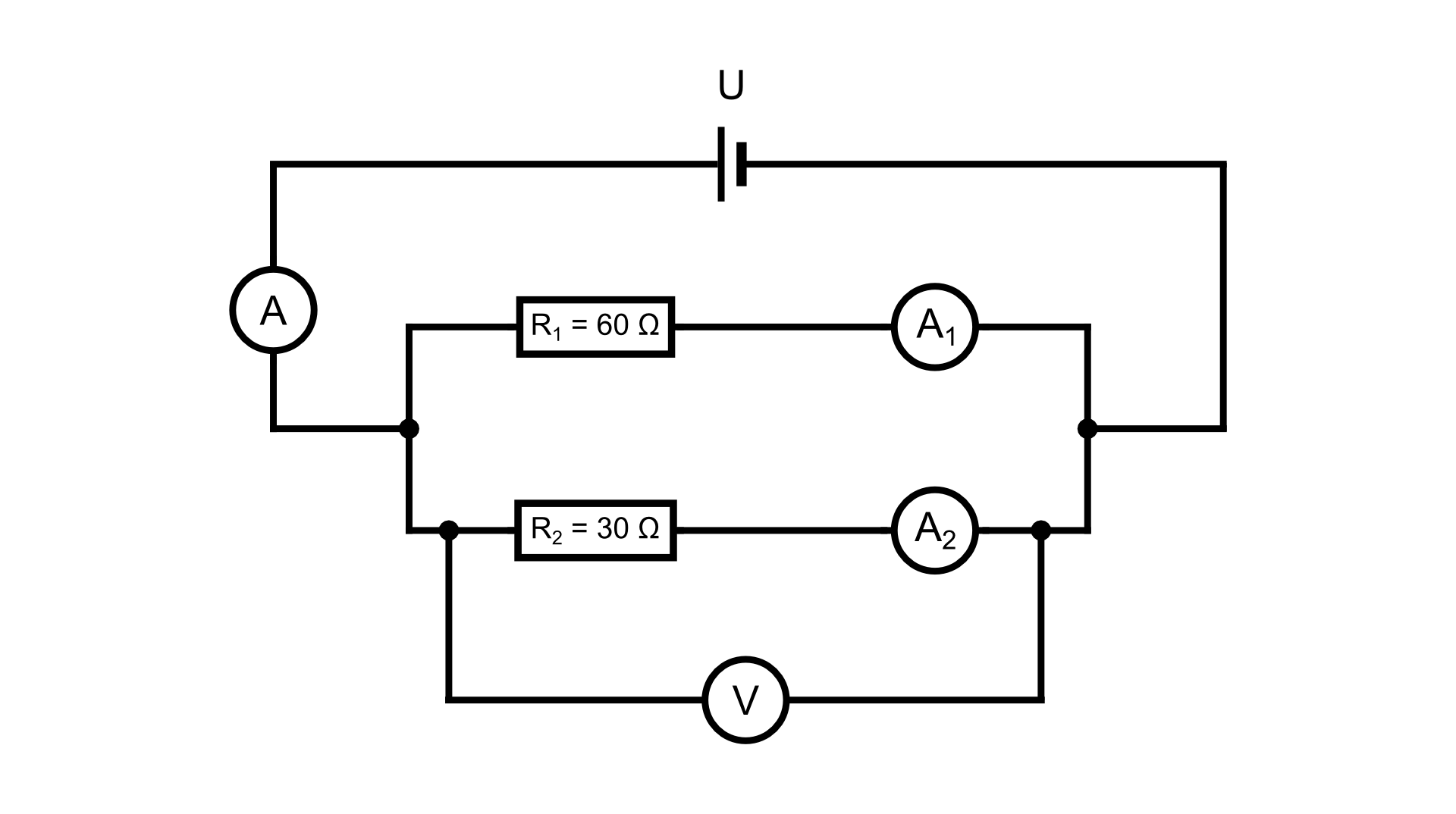
Na podstawie danych zawartych na schemacie oblicz, jakie będą wskazania mierników w obwodzie elektrycznym. Amperomierz $A_{1}$ wskazuje $0,5 A$ .

R5icgTCSq9ASB1

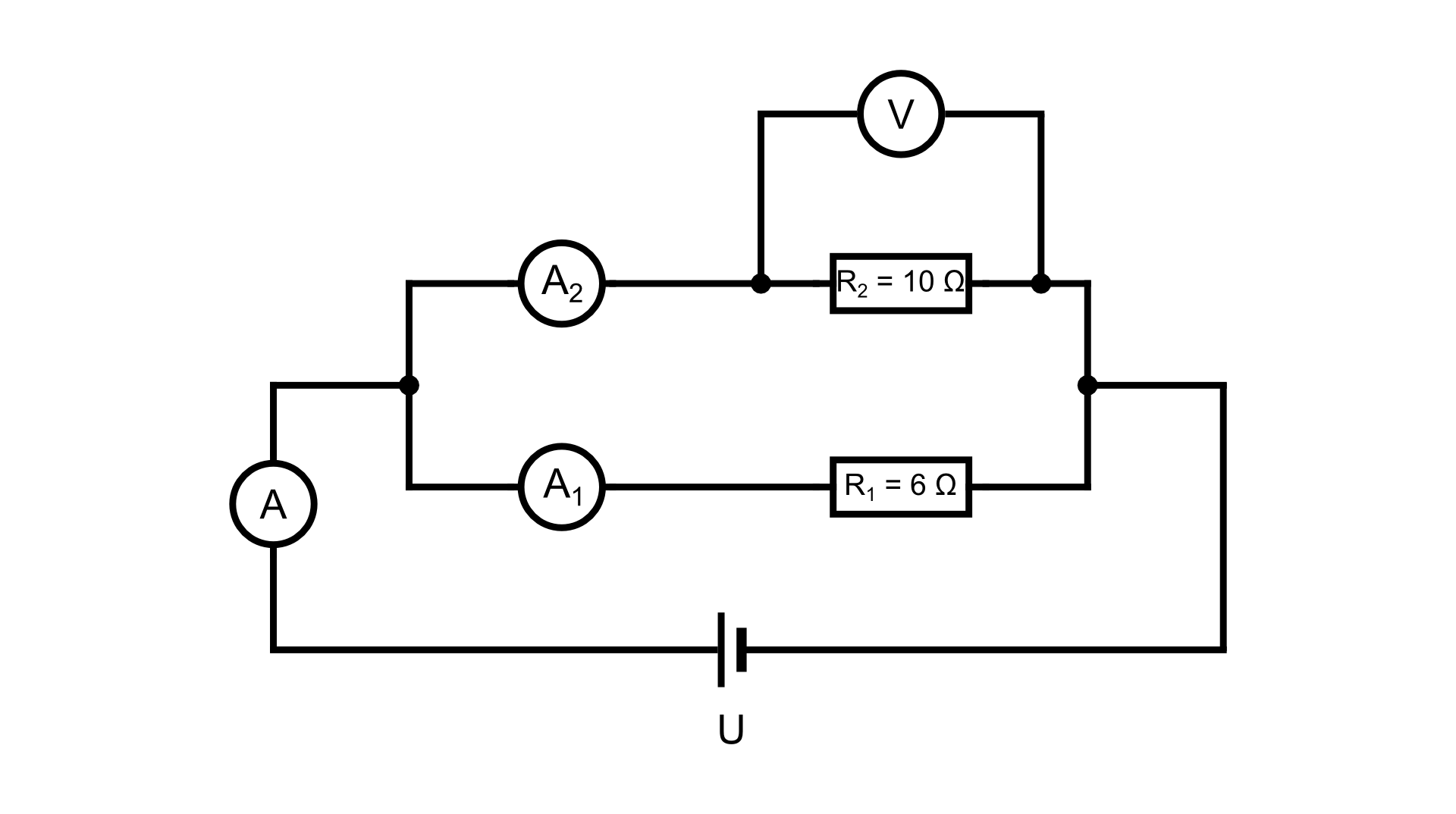
Połączenie równoległe - przykład1 — Źródło: Krzysztof Jaworski, licencja: CC BY 3.0.

Wzór:
$I = \frac{U}{R}$
Dane:
$R_{1} = 6 Ω$
$R_{2} = 10 Ω$
$I_{1} = 0,5 A$
Szukane:
$I = ?$
$I_{2} = ?$
$U = ?$
Obliczenia:
$U = 0,5 A \cdot 6 Ω = 3 V$
$I_{2} = \frac{3 V}{10 Ω} = 0,3 A$
$I = I_{1} + I_{2}$
$I = 0,5 A + 0,3 A = 0,8 A$
Odpowiedź:
Woltomierz wskazuje $3 V$ , amperomierz $A_{2}$ – 0,3 $A$ , natomiast amperomierz $A_{1}$ – $0,8 A$ .

R1Q4jh556QLLC1

Połączenie równoległe - ćwiczenie aktywizujące2 — Źródło: Krzysztof Jaworski, licencja: CC BY 3.0.

Ćwiczenie 4.1

RkNSmlPTFW3Es1

Na podstawie danych zawartych na schemacie obwodu elektrycznego oblicz wskazania mierników. Amperomierz $A_{2}$ wskazuje 0,1 A.
Wskaż prawidłowe odpowiedzi.

Amperomierz $A_{1}$ wskazuje wartość 0,05 A.
Amperomierz $A$ wskazuje wartość 0,15 A.
Woltomierz wskazuje wartość 6 V.
Amperomierz $A_{1}$ wskazuje wartość 0,5 A.

Źródło: Magdalena Grygiel <Magdalena.Grygiel@up.wroc.pl>, licencja: CC BY 3.0.

Przykład 4

Na podstawie schematu obwodu elektrycznego oblicz:

napięcie wytwarzane przez baterię;
natężenie prądu płynącego przez opornik;
opór opornika $R$ .

RWDdnqDOmLBvr1

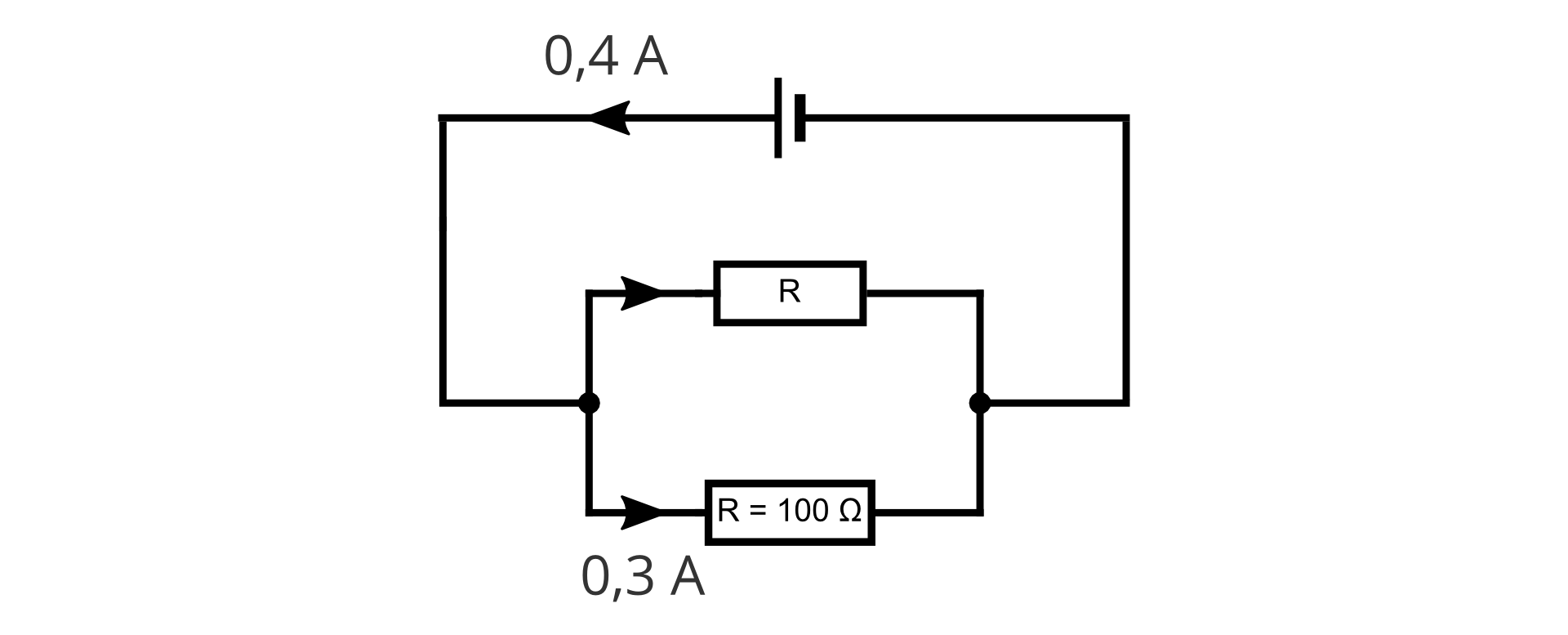
Połączenie równoległe - przykład 2.3 — Źródło: Krzysztof Jaworski, licencja: CC BY 3.0.

Zależności:
$U = I_{1} \cdot R_{1}$
$I = I_{1} + I_{2}$
$R = \frac{U}{I_{2}}$
Dane:
$I = 0,4 A$
$I_{1} = 0,3 A$
$R_{1} = 100 Ω$
Szukane:
$U = ?$
$I_{2} = ?$
$R = ?$
Obliczenia:
$U = 0,3 A \cdot 100 Ω = 30 V$
$0,3 A + I_{2} = 0,4 A$
$I_{2} = 0,4 A - 0,3 A = 0,1 A$
$R = \frac{30 V}{0,1 A} = 300 Ω$

Przykład 5

Odpowiedź:
Bateria wytwarza napięcie $30 V$ . Natężenie prądu płynącego przez opornik jest równe $0,1 A$ . Opór opornika wynosi $300 Ω$ .

Ri76NTwy7oE4Q1

Połączenie równoległe - ćwiczenie aktywizujące3 — Źródło: Krzysztof Jaworski, licencja: CC BY 3.0.

Ćwiczenie 5.1

RO8ebY38akq611

Korzystając z danych umieszczonych na schemacie obwodu elektrycznego uzupełnij puste miejsca.

Oporniki są połączone ....................... Natężenie prądu płynącego przez opornik $R_{2}$ jest równe ............. Bateria wytwarza napięcie ............. Opór opornika $R$ wynosi ............ Ω. Opór zastępczy jest ................ niż 2 Ω.

Źródło: Magdalena Grygiel <Magdalena.Grygiel@up.wroc.pl>, licencja: CC BY 3.0.

ime5s9ZIxT_d5e846

Podsumowanie:

Pierwsze prawo Kirchhoffa: suma natężeń prądów wpływających do węzła i suma natężeń prądów z niego wypływających są sobie równe.
$I = I_{1} + I_{2}$
Napięcie przyłożone do oporników połączonych równolegle i napięcie w poszczególnych opornikach mają taką samą wartość.
Aby obliczyć odwrotność oporu całkowitego (zastępczego $R$ ) odbiorników połączonych równolegle należy dodać do siebie odwrotności oporu poszczególnych odbiorników ( $R_{n}$ ).
$\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \dots$

Praca domowa

Polecenie 1.1

W różnych instalacjach elektrycznych znajdują się bezpieczniki. Wyszukaj w dostępnych ci źródłach (książki, internet), jaką rolę odgrywa bezpiecznik w instalacji. Opisz, jak działa to urządzenie.

ime5s9ZIxT_d5e901

Biogram

Gustaw Robert Kirchhoff

R1DBWVk0YCwjm1

Gustaw Robert Kirchhoff

12.03.1824–17.10.1887

Niemiecki fizyk o szerokich zainteresowaniach badawczych. Współtwórca analizy spektralnej, czyli określania składu chemicznego (np. mieszaniny pierwiastków) za pomocą analizy światła emitowanego przez substancje o wysokiej temperaturze. W 1845 r. opublikował prawa dotyczące przepływu prądu elektrycznego i tym samym poszerzył odkrycia Georga Ohma.

ime5s9ZIxT_d5e1001

Zadania podsumowujące lekcję

Ćwiczenie 6

R1OuhWb4v8QfP1

Uzupełnij puste miejsca wybierając brakujące elementy z listy.

może doprowadzić, równolegle, szeregowo, nie może doprowadzić

Samochodowa instalacja elektryczna może być zasilana akumulatorem o napięciu 12 V (głównie auta osobowe) lub 24 V (niektóre auta ciężarowe). Żarówki znajdujące się w reflektorach są połączone ............................................ .
Usunięcie lub przepalenie się jednej z nich ............................................ do zgaśnięcia pozostałych.

Źródło: Magdalena Grygiel <Magdalena.Grygiel@up.wroc.pl>, licencja: CC BY 3.0.

R1FXTIeU471w61

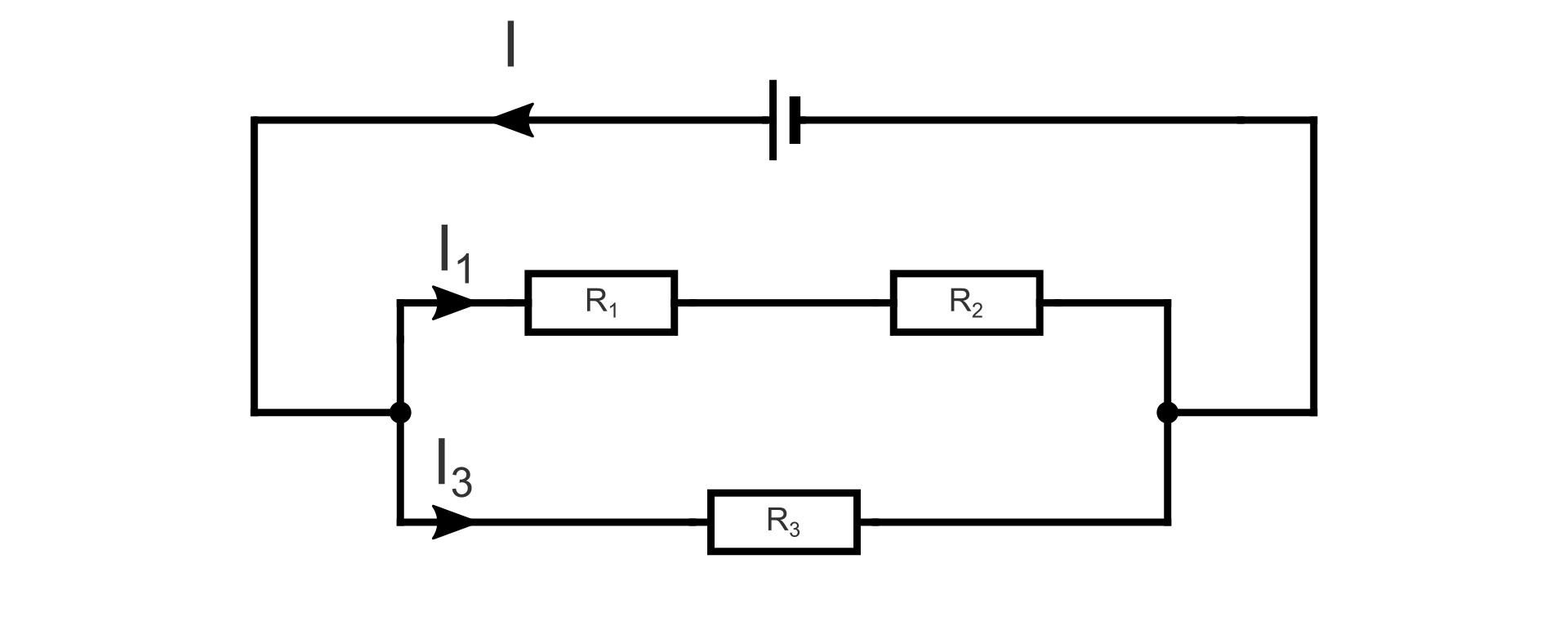
Połączenie równoległe - zadanie — Źródło: Krzysztof Jaworski, licencja: CC BY 3.0.

Ćwiczenie 7.1

Rl2v23lCjxhoT1

Oceń prawdziwość poniżśzych zdań.

	Prawda	Fałsz
Oporniki $R_{1}$ i $R_{2}$ są połączone z opornikiem $R_{3}$ równolegle.	□	□
Napięcie przyłożone do końców opornika $R_{3}$ jest równe napięciu ogniwa.	□	□
Wszystkie oporniki są połączone równolegle.	□	□
Dla tego obwodu prawdziwa jest zależność: $I_{1} = I_{3}$ .	□	□

Źródło: Magdalena Grygiel <Magdalena.Grygiel@up.wroc.pl>, licencja: CC BY 3.0.

Ćwiczenie 8

R1DNHFh0zRmKD1

Opornik o oporach $R_{1} = 12 Ω$ i $R_{2} = 6 Ω$ połączono równolegle i podłączono pod napięcie $U = 24 V$ . Oblicz opór zastępczy ( $R$ ) i natężenie prądu płynącego przez każdy opornik.

$R = 4 Ω$ , $I_{1} = 2 A$ , $I_{2} = 4 A$
$R = 18 Ω$ , $I_{1} = 3 A$ , $I_{2} = 4 A$
$R = 4 Ω$ , $I_{1} = 0,5 A$ , $I_{2} = 0,25 A$
$R = 18 Ω$ , $I_{1} = 0,5 A$ , $I_{2} = 0,25 A$

Źródło: Magdalena Grygiel <Magdalena.Grygiel@up.wroc.pl>, licencja: CC BY 3.0.

Ćwiczenie 9

R1C1zaoghN3zD1

W obwodzie elektrycznym znajduje się dziesięć żarówek o oporze R = 10 Ω każda oraz bateria o napięciu U = 4,5 V. Żarówki połączone są równolegle. Wybierz prawidłowe stwierdzenia.

Opór całkowity wynosi 100 Ω.
Napięcie na każdej żarówce jest równe 4,5 V.
Natężenie prądu płynącego przez każdą żarówkę jest mniejsze niż 0,5 A.

Źródło: Magdalena Grygiel <Magdalena.Grygiel@up.wroc.pl>, licencja: CC BY 3.0.

Połączenie szeregowe odbiorników

Praca prądu elektrycznego

Połączenie równoległe odbiorników

1. Połączenie równoległe – podstawy teoretyczne

2. Połączenie równoległe – rozwiązywanie zadań

Podsumowanie:

Biogram

Gustaw Robert Kirchhoff

Zadania podsumowujące lekcję