Prezentacja multimedialna
Polecenie 1
Zapoznaj się z prezentacją multimedialną, a następnie wykonaj polecenia zamieszczone pod nią.
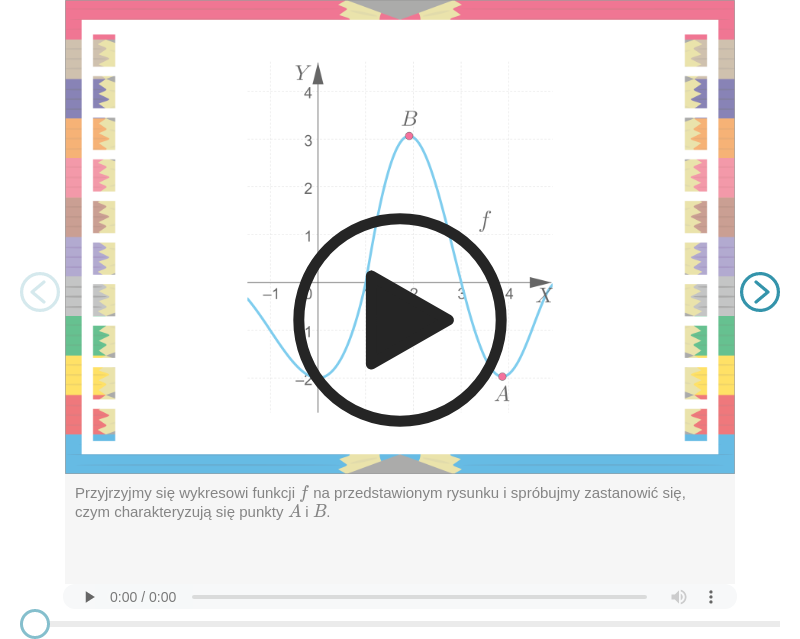
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D11MLy0BZ
Polecenie 2
Łączenie par. Na podstawie informacji zawartych w filmie zaznacz czy zdanie jest prawdziwe czy fałszywe.. Funkcja ma w punkcie maksimum lokalne właściwe równe , gdy można wskazać takie otoczenie punktu , że dla każdego argumentu z tego otoczenia .. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja ma w punkcie minimum lokalne właściwe równe , gdy można wskazać takie otoczenie punktu , że dla każdego argumentu z tego otoczenia .. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja ma w punkcie maksimum lokalne właściwe równe , gdy można wskazać takie otoczenie punktu , że dla każdego argumentu z tego otoczenia .. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja ma w punkcie maksimum lokalne właściwe równe , gdy można wskazać takie otoczenie punktu , że dla każdego argumentu z tego otoczenia .. Możliwe odpowiedzi: Prawda, Fałsz
Na podstawie informacji zawartych w prezentacji zaznacz czy zdanie jest prawdziwe czy fałszywe.
| Zdanie | Prawda | Fałsz |
| Funkcja ma w punkcie maksimum lokalne właściwe równe , gdy można wskazać takie otoczenie punktu , że dla każdego argumentu z tego otoczenia . | □ | □ |
| Funkcja ma w punkcie minimum lokalne właściwe równe , gdy można wskazać takie otoczenie punktu , że dla każdego argumentu z tego otoczenia . | □ | □ |
| Funkcja ma w punkcie maksimum lokalne właściwe równe , gdy można wskazać takie otoczenie punktu , że dla każdego argumentu z tego otoczenia . | □ | □ |
| Funkcja stała ma w każdym punkcie ekstremum lokalne właściwe. | □ | □ |
Polecenie 3
Korzystając z definicji pokażemy, że funkcja ma ekstremum lokalne w punkcie .