Przeczytaj

Przykład 1

Dla każdej liczby rzeczywistej dodatniej $a$ , $b$ zachodzi nierówność $\frac{a}{b} + \frac{b}{a} \geq 2$ .

Rozwiązanie:

Sprowadźmy ułamki algebraiczne do wspólnego mianownika $\frac{a^{2} + b^{2}}{a b} \geq 2$ .

Pomnóżmy obie strony nierówności przez $a \cdot b$ :

$\frac{a^{2} + b^{2}}{a b} \geq 2 | \cdot a \cdot b$ , gdzie $a \cdot b > 0$ .

Zauważmy , że iloczyn liczb dodatnich $a$ , $b$ jest liczbą dodatnią, czyli zwrot nierówności nie zmieni się

$a^{2} - 2 a b + b^{2} \geq 0$ ,

${(a - b)}^{2} \geq 0$ .

Nierówność jest prawdziwa, bo kwadrat dowolnej liczby rzeczywistej jest nieujemny więc i nierówność $\frac{a}{b} + \frac{b}{a} \geq 2$ jest prawdziwa.

Przykład 2

Wykaż, że jeśli $x > 0$ , to $\frac{10 x^{2} + x + 10}{x} \geq 21$ .

Rozwiązanie:

Dowód nie wprost:

Załóżmy, że $\frac{10 x^{2} + x + 10}{x} < 21$ dla $x > 0$ .

Pomnóżmy obie strony nierówności przez $x$ .

Znak nierówności nie ulegnie zmianie, ponieważ $x > 0$ .

Zatem $10 x^{2} + x + 10 < 21 x$ ,

$10 x^{2} - 20 x + 10 < 0$ ,

${(x - 1)}^{2} < 0$ .

Nierówność ${(x - 1)}^{2} < 0$ jest sprzeczna, bo kwadrat dowolnej liczby rzeczywistej jest nieujemny.

Skoro nierówność $\frac{10 x^{2} + x + 10}{x} < 21$ dla $x > 0$ okazała się fałszywa, to nierówność $\frac{10 x^{2} + x + 10}{x} \geq 21$ jest prawdziwa dla $x > 0$ .

Algorytmy rozwiązywania nierówności wymiernych z wielomianem stopnia drugiego w liczniku

$I$ sposób:

Wyznaczamy dziedzinę nierówności wymiernejdziedzina nierówności wymiernejdziedzinę nierówności wymiernej.
Sprowadzamy nierówność do postaci ogólnej - przenosimy wszystkie wyrażenia na jedną stronę nierówności.
Wykonujemy wskazane działania.
Nierówność wymierną rozwiązujemy doprowadzając ją do równoważnej postaci wielomianowej przy wyznaczonej dziedzinie nierówności wymiernejdziedzina nierówności wymiernejdziedzinie nierówności wymiernej (zastępujemy iloraz iloczynem z uwzględnieniem założeń).
Wyznaczamy pierwiastki wielomianupierwiastek wielomianupierwiastki wielomianu oraz szkicujemy wykres.
Z wykresu odczytujemy zbiór rozwiązań danej nierówności.
Wyznaczamy rozwiązanie nierówności wymiernej uwzględniając dziedzinę.

$II$ sposób:

Wyznaczamy dziedzinę nierówności wymiernejdziedzina nierówności wymiernejdziedzinę nierówności wymiernej.
Mnożymy obustronnie nierówność przez kwadrat mianownika lub przez inne wyrażenia, których znak jest jednoznacznie określony.
Wykonujemy wskazane działania.
Wyznaczamy pierwiastki wielomianu oraz szkicujemy wykres
Z wykresu odczytujemy zbiór rozwiązań danej nierówności.
Wyznaczamy rozwiązanie nierówności wymiernej uwzględniając dziedzinę.

W podanych poniżej przykładach będziemy korzystać z poniższego twierdzenia.

o równoważności nierówności

Twierdzenie: o równoważności nierówności

$\frac{W_{1} (x)}{W_{2} (x)} > 0 \Leftrightarrow W_{1} (x) \cdot W_{2} (x) > 0 \land W_{2} (x) \neq 0$ ,

$\frac{W_{1} (x)}{W_{2} (x)} < 0 \Leftrightarrow W_{1} (x) \cdot W_{2} (x) < 0 \land W_{2} (x) \neq 0$ ,

$\frac{W_{1} (x)}{W_{2} (x)} \geq 0 \Leftrightarrow W_{1} (x) \cdot W_{2} (x) \geq 0 \land W_{2} (x) \neq 0$ ,

$\frac{W_{1} (x)}{W_{2} (x)} \leq 0 \Leftrightarrow W_{1} (x) \cdot W_{2} (x) \leq 0 \land W_{2} (x) \neq 0$ .

Zatem przy rozwiązywaniu nierówności wymiernych często skorzystamy z twierdzenia, że iloraz i iloczyn tych samych wyrażeń mają ten sam znak.

Ważne!

Rozwiązując nierówność wymierną, pamiętajmy o wyznaczeniu dziedziny nierówności wymiernejdziedzina nierówności wymiernejdziedziny nierówności wymiernej.

Przykład 3

Rozwiążemy nierówność $\frac{x^{2} - 10 x + 25}{x^{4} - 9 x^{2}} \leq 0$ .

Rozwiązanie:

Podajmy konieczne założenie: $x^{4} - 9 x^{2} \neq 0$ ,

$x^{2} (x^{2} - 9) \neq 0$

$x^{2} \neq 0$ , $x^{2} - 9 \neq 0$

$x^{2} \neq 0$ , $x^{2} \neq 9$

$x \neq 0$ , $x \neq - 3$ , $x \neq 3$

Dziedziną nierówności wymierej jest $D = ℝ ∖ \{- 3; 0; 3\}$ .

Dla nierówności $\frac{x^{2} - 10 x + 25}{x^{4} - 9 x^{2}} \leq 0$

przedstawmy licznik i mianownik w postaci iloczynowej.

$\frac{{(x - 5)}^{2}}{x^{2} (x - 3) (x + 3)} \leq 0$

Skorzystajmy z poniższej równoważności:

$\frac{W_{1} (x)}{W_{2} (x)} \leq 0 \Leftrightarrow W_{1} (x) \cdot W_{2} (x) \leq 0 \land W_{2} (x) \neq 0$ ,

czyli zapiszmy nierówność w postaci równoważnej nierówności iloczynowej

$x^{2} {(x - 5)}^{2} (x - 3) (x + 3) \leq 0 \land x \neq -3$ , $x \neq 0$ , $x \neq 3$ .

Wielomian $W (x) = x^{2} {(x - 5)}^{2} (x - 3) (x + 3)$ ma dwa pierwiastkipierwiastek wielomianupierwiastki dwukrotne: $0$ ; $5$ oraz dwa pierwiastkipierwiastek wielomianupierwiastki jednokrotne: $(- 3)$ ; $3$ .

R1Q5qKroPwhHG

Na ilustracji przedstawiony jest wykres, który prezentuje rozwiązanie rozpatrywanej nierówności. Na osi X zaznaczone są cztery rozwiązania -3, 0 , 3 i 5. Argumenty -3,0,3 są zaznaczone niezamalowanymi kropkami, a argument równy 5 jest zaznaczony zamalowaną kropką. Wykres zaczynamy rysować od góry prawej stronie docieramy do x=5 i odbijamy się od niego i następnie prowadzimy linie do argumentu 3 przez który przechodzimy pod oś X. Następnie dochodzimy do punktu 0 i znów odbijamy się od niego ,aby dotrzeć do argumentu -3 i przeciąć go tak, że wykres znajduje się nad osią X. Przydziały, które są nad osią X oznaczamy symbolicznie plusami , a te które są pod nią minusami.

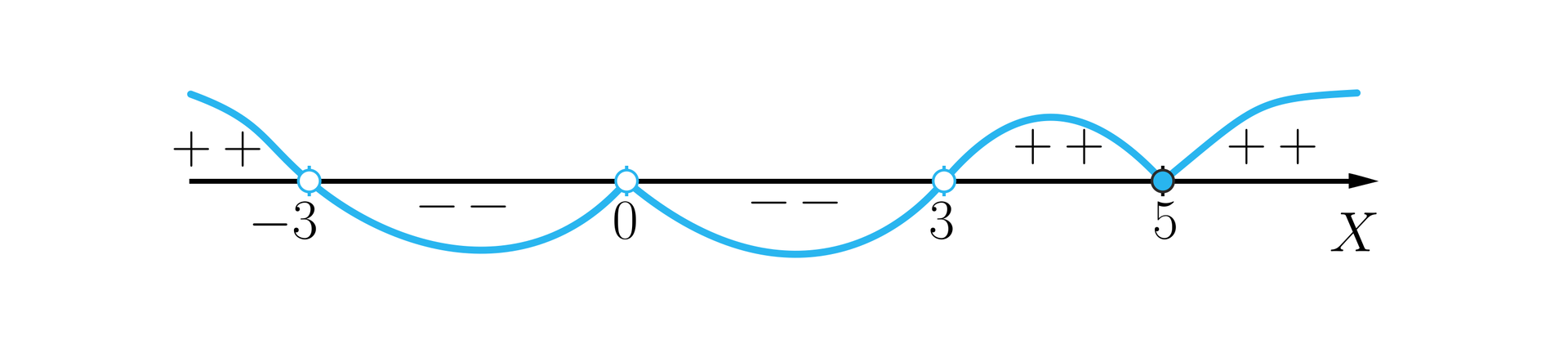
Odpowiedź: Rozwiązaniem nierówności jest zbiór $(- 3; 0) \cup (0; 3) \cup \{5\}$ .

Dla zainteresowanych

Nierównośc wielomianową $x^{2} {(x - 5)}^{2} (x - 3) (x + 3) \leq 0$ , gdzie $x \neq - 3$ , $x \neq 0$ , $x \neq 3$ możemy rozwiązać za pomocą tzw. „siatki znaków”.

RcveaOylfrc7U

Tabela składa się z wierszy po lewej stronie zawierających kolejne składowe nierówności, natomiast nagłówki kolumn to przedziały kolejno pierwszy od minus nieskończoności do -3, -3 , od -3 do 0, 0 , od 0 do 3, 3, od 3 do 5 , 5 oraz od 5 do plus nieskończoności. Pierwszym rozważanym składnikiem jest x +3 . Na przedziale minus nieskończoność do -3 podany dwumian jest ujemny, w -3 przyjmuje miejsce serowe , na przedziale -3 do 0 jest dodatni i tak do końca na każdym przedziale i nie przyjmuje już innych miejsc zerowych. Kolejny jest jednomian x do kwadratu który na przedziale minus nieskończoność jest dodatni, w punkcie 3 nie osiąga miejsca zerowego jest dodatni na przedziale od -3 do 0, w 0 ma miejsce zerowe, na przedziale od 0 do 3 jest dodatni, nie przyjmuje w 3 miejsca zerowego na przedziale od 3 do 5 jest dodatni oraz nie ma miejsca zerowego w 5 i na przedziale od 5 do plus nieskończoności tez jest dodatni. Kolejnym składnikiem nierówności jest dwumian x -3 który na przedziale od minus nieskończoności przyjmuje wartości ujemne, nie osiąga w -3 miejsca zerowego, na przedziale od -3 do 0 nadal jest ujemny i w 0 również nie ma miejsca zerowego, na przedziale od 0 do 3 jest ujemny i osiąga miejsce zerowe w punkcie 3 , aby następnie na przedziale od 3 do 5 przyjmować wartości dodatnie nie osiąga już miejsca zerowego w 5 a na przedziale od 5 do plus nieskończoności jest dodatnia. Przedostatni składni to x -5 podniesione do kwadratu. Na pierwszym przedziale dwumian przyjmuje wartości dodatnie nie osiąga miejsca zerowego w -3 , na przedziale od -3 do 0 jest dodani nie osiąga miejsca zerowego w 0 , na przedziale od 0 do 3 jest dodatni nie osiąga miejsca zerowego w 3, na przedziale od 3 do 5 jest dodatni osiąga miejsce zerowe w 5 oraz od 5 do plus nieskończoności jest dodatni. Ostatni wiersz poświęcony jest całemu wielomianowi z zadania, zatem analizując po kolei znaki składowych na każdym przedziale dostajemy , że na przedziale od minus nieskończoności wielomian jest dodatni, w miejsce -3 wpisujemy duży X, na przedziel od -3 do 0 jest wielomian ujemny, dla 0 mamy duży X, na przedziale od 0 do 3 wielomian jest ujemny , dla 3 mamy duży X, na przedziale od 3 do 5 jest dodatni, dla 5 mamy 0 a na ostatnim przedziale od 5 do plus nieskończoności wielomian jest dodatni.

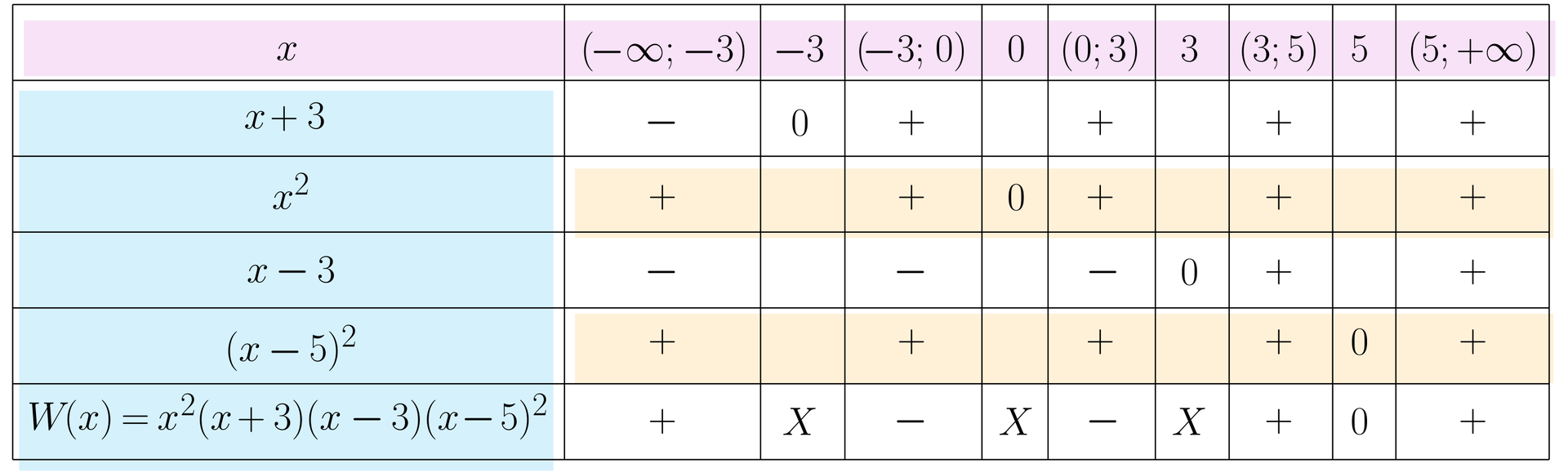
Zatem rozwiązaniem nierówności jest zbiór $(- 3; 0) \cup (0; 3) \cup \{5\}$ .

Przykład 4

Wyznaczmy zbiór rozwiążań nierówności $\frac{7 x^{2} - 16 x - 15}{- x^{2} + 4 x - 3} > 1$ .

Rozwiązanie:

Podajmy konieczne założenie: $- x^{2} + 4 x - 3 \neq 0$

$- (x - 1) (x - 3) \neq 0$

$x \neq 1$ , $x \neq 3$

$D = ℝ ∖ \{1; 3\}$ .

Dla nierówności

$\frac{7 x^{2} - 16 x - 15}{- x^{2} + 4 x - 3} > 1$ .

przedstawmy licznik i miamnownik ułamka algebraicznegoułamek algebraicznyułamka algebraicznego w postaci iloczynowej

$\frac{7 (x + \frac{5}{7}) (x - 3)}{- (x - 1) (x - 3)} > 1$ .

Po skróceniu wyrażenie $x - 3$ nierównośc ma postać

$\frac{7 (x + \frac{5}{7})}{- (x - 1)} > 1$ ,

$\frac{7 (x + \frac{5}{7})}{- (x - 1)} > 1 | \cdot (- 1)$ .

Rozwiążmy nierówność mnożąc obie strony nierówności przez ${(x - 1)}^{2} > 0$ :

$\frac{7 (x + \frac{5}{7})}{(x - 1)} < - 1 | \cdot {(x - 1)}^{2}$ ,

$7 (x + \frac{5}{7}) (x - 1) < - {(x - 1)}^{2}$ ,

$7 (x + \frac{5}{7}) (x - 1) + {(x - 1)}^{2} < 0$ .

Wyłaczmy czynnik $x - 1$ przed nawias

$(x - 1) [7 (x + \frac{5}{7}) + x - 1] < 0$ ,

$(x - 1) [7 x + 5 + x - 1] < 0$ ,

$(x - 1) (8 x + 4) < 0$ .

Uwzględniając dziedzinę nierówności wymiernej $D = ℝ ∖ \{1; 3\}$ , sporządźmy szkic wykresu funkcji wielomianowej $R (x) = 8 (x - 1) (x + \frac{1}{2})$ , gdzie pierwiastkami jednokrotnymi są liczby: $(- \frac{1}{2})$ , $1$ .

Rg3lsmcdCmA3T

Na ilustracji przedstawiony jest wykres rozwiązań nierówności. Na osi X zaznaczone są trzy argumenty -1/2, 1 oraz 3 , gdzie wszystkie z nich są zaznaczone otwartymi kropkami. Wykres poprowadzony jest od góry i przechodzi przez 1 , następnie przechodzi przez -1/2 przez co wykres znów pojawia się na górze. Przedziały, gdzie wykres funkcji jest na osią X zaznaczony jest plusami , na przedziale od -1/2 do 1 gdzie wykres jest pod osią X i zaznaczony jest minusami.

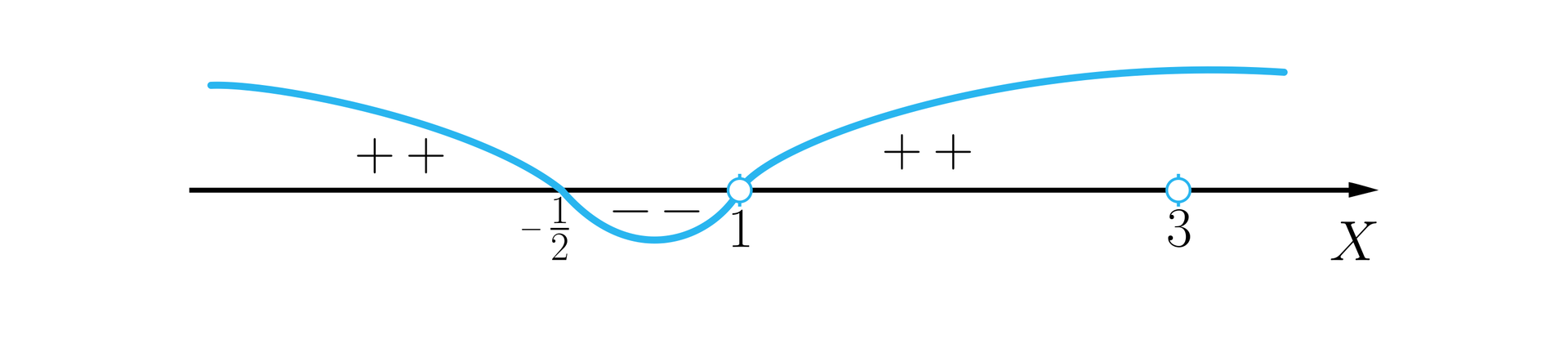
Odpowiedź: Zbiorem rozwiązań nierówności $\frac{7 x^{2} - 16 x - 15}{- x^{2} + 4 x - 3} > 1$ jest przedział $(- \frac{1}{2}; 1)$ .

Ważne!

Zwróćmy uwagę na to , że przy rozwiązywaniu nierówności wymiernej drugim sposobem, nie możemy mnożyć obustronnie nierówności przez mianownik wyrażenia wymiernego, jeśli nie wiemy jaki on ma znak, czy ujemny, czy dodatni. Jeśli znak mianownika byłby ujemny, to po pomnożeniu nierówności przez ten mianownik, musielibyśmy zmienić zwrot nierówności.

Przykład 5

Rozwiążemy nierówność $\frac{- 3 x^{2} + 5 x}{x} \geq 3 x^{2} + 10 x - 5$ .

Rozwiązanie:

Podajmy założenie: $x \neq 0$ , czyli $D = ℝ ∖ \{0\}$ .

Przedstawmy licznik i mianownik ułamka algebraicznego w postaci iloczynowej

$\frac{- 3 x (x - \frac{5}{3})}{x} \geq 3 x^{2} + 10 x - 5$ .

Skróćmy ułamek algebraiczny, otrzymując nierówność wielomianową $- 3 x + 5 \geq 3 x^{2} + 10 x - 5$ ,

Pomnóżmy nierówność obustronnie przez $(- 1)$ :

$- 3 x^{2} - 13 x + 10 \geq 0 | \cdot (- 1)$ ,

$3 x^{2} + 13 x - 10 \leq 0$ ,

$3 (x - \frac{2}{3}) (x + 5) \leq 0$ .

Uwzględniając dziedzinę nierówności wymiernej $D = ℝ ∖ \{0\}$ sporządźmy szkic wykresu funkcji $S (x) = 3 (x - \frac{2}{3}) (x + 5)$ , gdzie pierwiastkami jednokrotnymi są liczby: $(- 5)$ ; $\frac{2}{3}$ .

RdlSlZl6iDPyi

Ilustracja przedstawia oś X z zaznaczonymi trzema argumentami -5, 0, 2/3. Wykres jest rysowany od góry po prawej stronie, przechodzi najpierw przez argument 2/3 a następnie przez argument -5. Zatem wykres jest nad osią X na przedziale od minus nieskończoności do -5 oraz od 2/3 do plus nieskończoności i jest zaznaczony plusami. Przedział od -5 do 2/3 jest pod osią X i jest zaznaczony minusami.

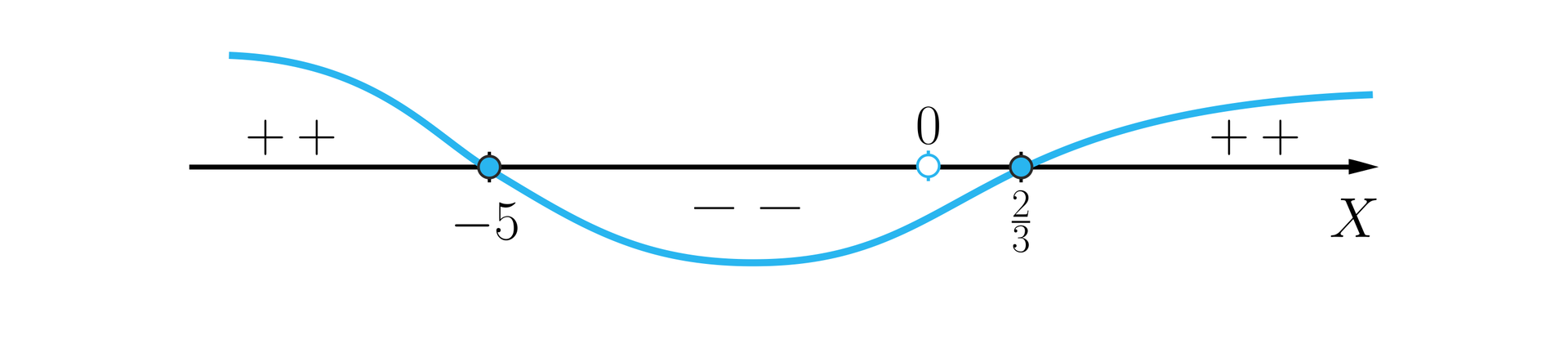
Odpowiedź: Rozwiązaniem nierówności jest zbiór $⟨- 5; 0) \cup (0; \frac{2}{3}⟩$ .

Słownik

dziedzina nierówności wymiernej

dziedziną nierówności wymiernej są wszystkie liczby rzeczywiste za wyjątkiem pierwiastków wielomianu $W_{2} (x)$ znajdującego się w mianowniku danego wyrażenia $\frac{W_{1} (x)}{W_{2} (x)}$

$D = ℝ ∖ \{x : W_{2} (x) = 0\}$ .

ułamek algebraiczny

ułamkiem algebraicznym jednej zmiennej rzeczywistej $x$ nazywamy wyrażenie $\frac{W_{1} (x)}{W_{2} (x)}$ , którego licznikiem jest wielomian $W_{1} (x)$ , a mianownikiem jest wielomian $W_{2} (x)$ i $W_{2} (x) \neq 0$

pierwiastek wielomianu

Pierwiastkiem wielomianu $W (x)$ nazywamy liczbę rzeczywistą $a$ , dla której $W (a) = 0$

Wprowadzenie

Galeria zdjęć interaktywnych

Algorytmy rozwiązywania nierówności wymiernych z wielomianem stopnia drugiego w liczniku

$I$ sposób:

$II$ sposób:

Słownik

Wprowadzenie

Galeria zdjęć interaktywnych

Przeczytaj

Algorytmy rozwiązywania nierówności wymiernych z wielomianem stopnia drugiego w liczniku

I sposób:

II sposób:

Słownik

$I$ sposób:

$II$ sposób: