Czworokąt, którego przeciwległe boki są równoległe, nazywany równoległobokiem.

Niech $ABCD$ będzie czworokątem wypukłym oraz niech $E$ będzie punktem przecięcia przekątnych $AC$ i $BD$.

R1beAXUde2aAE

Na ilustracji przedstawiono równoległobok $ABCD$, którego przekątne przecinają się w punkcie E.

Wówczas następujące warunki są równoważne:

1. proste $AB$ i $CD$ są równoległe oraz proste $BC$ i $DA$ są równoległe;

2. $\left|AB\right|=\left|CD\right|$ oraz $\left|BC\right|=\left|DA\right|$;

3. $\left|AB\right|=\left|CD\right|$ oraz proste $AB$ i $CD$ są równoległe;

4. $\left|AE\right|=\left|EC\right|$ oraz $\left|BE\right|=\left|ED\right|$.

Punkt $M$ jest środkiem boku $BC$ trójkąta $ABC$. Wówczas $\left|\sphericalangle BAC\right|=90°$ wtedy i tylko wtedy, gdy $\left|AM\right|=\frac{1}{2}\left|BC\right|$.

R1XpqkgZmeKjc

Na ilustracji przedstawiono trójkąt prostokątny $ABC$, z kątem prostym przy wierzchołku A. Zaznaczono odcinek łączący wierzchołek A, z punktem M, który stanowi środek boku $BC$ trójkąta.

Rozwiązanie

Oznaczmy przez $D$ punkt symetryczny do punktu $A$ względem punktu $M$. Wówczas czworokąt $ABDC$ jest równoległobokiem:

RAc1lXhjRKQZd

Na ilustracji przedstawiono równoległobok $ABCD$, którego przekątne przecinają się w punkcie M.

Zauważmy, że jeżeli $\left|\sphericalangle BAC\right|=90°$ to również $\left|\sphericalangle ACD\right|=90°$. Wtedy trójkąty $BAC$ i $CDA$ są przystające, stąd $\left|AM\right|=\frac{1}{2}\left|AD\right|=\frac{1}{2}\left|BC\right|$.

Odwrotnie: jeżeli $\left|AM\right|=\frac{1}{2}\left|BC\right|$ to $\left|AD\right|=\left|BC\right|$ i trójkąty $BAC$ i $DCA$ są przystające, stąd wniosek, że kąty $BAC$ i $DCA$ są równe. Ponadto suma ich miar jest równa $180°$, więc miara każdego z nich musi być równa $90°$.

Punkty $K$ i $L$ są środkami boków $AC$ i $BC$ trójkąta $ABC$. Wówczas proste $KL$ i $AB$ są równoległe oraz $\left|KL\right|=\frac{1}{2}\left|AB\right|$

R1ONo38uRmoEw

Na ilustracji przedstawiono trójkąt $ABC$, o podstawie $AB$. Zaznaczono poziomy odcinek $KL$, łączący środki ramion trójkąta.

Rozwiązanie

R1dM0xqyoZupo

Na ilustracji przedstawiono trójkąt $ABC$, o podstawie $AB$. Zaznaczono poziomy odcinek $KL$, łączący środki ramion trójkąta. Odcinek $KL$ przedłużono o wartość jego długości i zaznaczono punkt S. Liniami przerywanymi punkt S połączono z wierzchołkiem C oraz wierzchołek B z punktem K.

Niech $S$ będzie obrazem symetrycznym punktu $K$ względem punktu $L$. Wówczas czworokąt $KBSC$ jest równoległobokiem, wobec tego odcinki $KC$ i $BS$ są równoległe i mają równą długość. Z założeń $\left|AK\right|=\left|KC\right|$, więc czworokąt $ABSK$ jest równoległobokiem, zatem proste $KL$ i $AB$ są równoległe, oraz $\left|KL\right|=\frac{1}{2}\left|KS\right|=\frac{1}{2}\left|AB\right|$.

Punkty $K$, $L$, $M$, $N$ są odpowiednio środkami boków $AB$, $BC$, $CD$, $DA$ czworokąta $ABCD$ (rysunek). Pokażemy, że $KLMN$ to równoległobok.

R1LxYuwXQMI60

Na ilustracji przedstawiono czworokąt $ABCD$. Zaznaczono cztery punkty. Punkt K stanowi środek boku $AB$, punkt L stanowi środek boku $BC$, punkt M stanowi środek boku $DC$, punkt N stanowi środek boku $AD$.

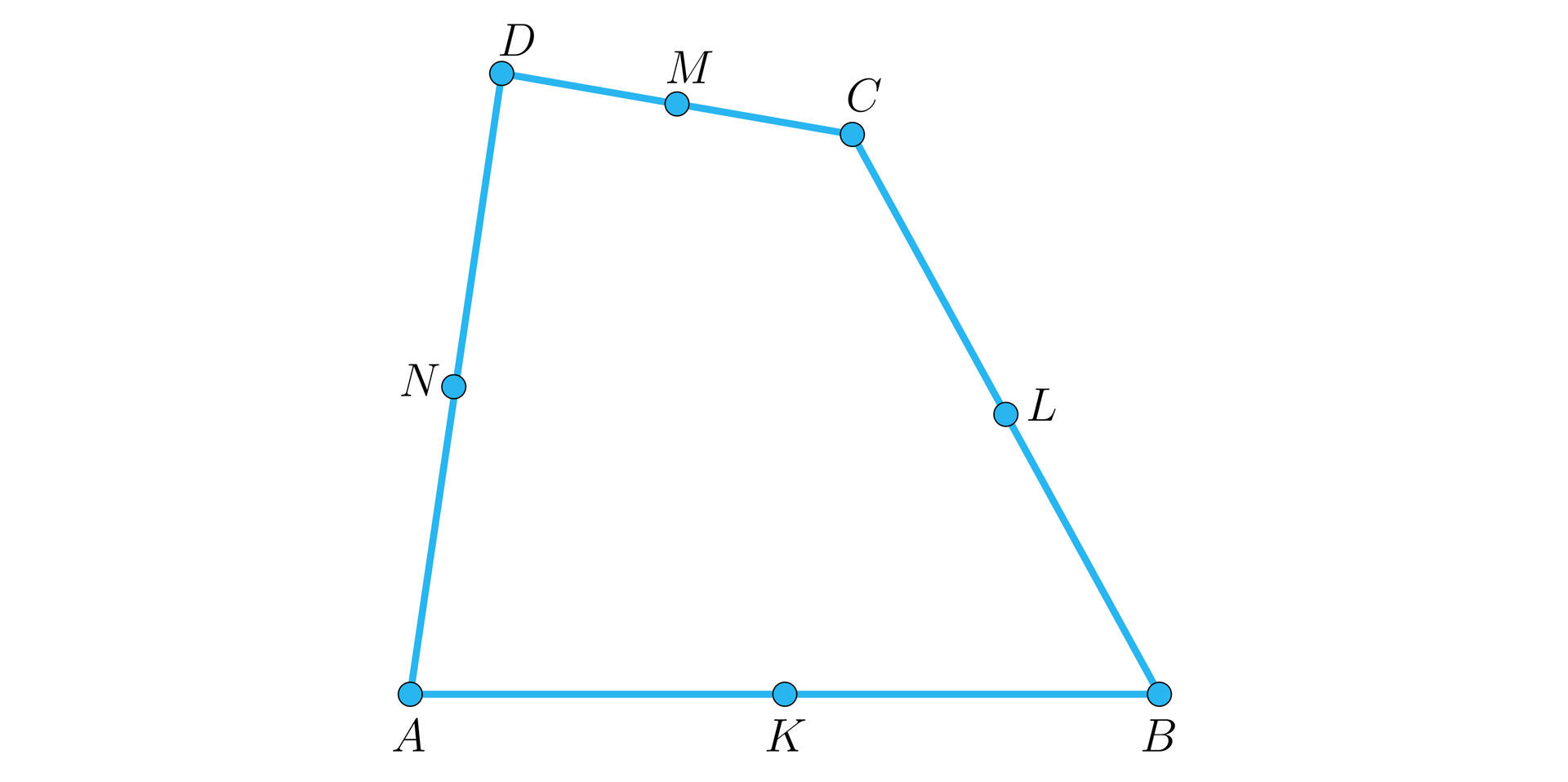
Rozwiązanie

R1IAV05spHbhx

Na ilustracji przedstawiono czworokąt $ABCD$. Zaznaczono cztery punkty. Punkt K stanowi środek boku $AB$, punkt L stanowi środek boku $BC$, punkt M stanowi środek boku $DC$, punkt N stanowi środek boku $AD$. Zielonym kolorem zaznaczono odcinki $LM$, $KN$, $BD$. Różowym kolorem zaznaczono odcinek $AC$, oraz $KL$.

Wystarczy, że wykorzystamy tezę poprzedniego przykładu analizując trójkąty $ABC$ i $ACD$. Otrzymamy, że odcinki $KL$ i $NM$ są równoległe do $AC$ oraz równe połowie tego odcinka, więc czworokąt (na podstawie własności $3$) jest równoległobokiem.

Podobnie, odcinki $ML$ i $NK$ są równoległe do odcinka $DB$ oraz równe połowie tego odcinka, więc czworokąt $KLMN$ jest równoległobokiem.

Po dwóch stronach rzeki o równoległych brzegach znajdują się dwa domki położone w punktach $A$ i $B$ (rysunek). W którym miejscu należy wybudować most $XY$, prostopadły do brzegów rzeki, aby droga łącząca oba domki i biegnąca przez most była najkrótsza?

R1Ow46ffGo044

Na ilustracji przedstawiono rzekę, której szerokość stanowi odległość od punktu X do Y. Po jednej stronie rzeki znajduje się domek w punkcie A, oraz po drugiej stronie znajduje się domek w punkcie B. Linią zaznaczono drogę łączącą kolejno punkty A, X, Y, B.

Rozwiązanie

R1TQb54awHJIj

Na ilustracji przedstawiono rzekę, której szerokość stanowi odległość od punktu X do Y. Po jednej stronie rzeki znajduje się domek w punkcie A, oraz po drugiej stronie znajduje się domek w punkcie B. Linią zaznaczono drogę łączącą kolejno punkty A, X, Y, B. Zaznaczono punkt C, taki że odległość $AX$, równa się odległości $CY$. Punkt B połączono z punktem C. W miejscu przecięcia odcinka $BC$ z prostą stanowiącą brzeg rzeki zaznaczono punkt Z. Linią przerywaną zaznaczono odcinek $ZD$, stanowiący szerokość rzeki.

Zastanowimy się, kiedy łamana $AXYB$ jest najkrótsza. Zauważmy, że brzegi rzeki są równoległe, więc jej szerokość, a więc długość mostu jest zawsze taka sama.

Możemy zatem pominąć długość mostu $XY$. Nasze zadanie polega więc na znalezieniu takiego miejsca przy brzegu rzeki, żeby suma długości odcinków $AX+YB$ była najmniejsza z możliwych.

Wyznaczmy taki punkt $C$, aby czworokąt $AXYC$ był równoległobokiem. Wtedy

$\left|AX\right|+\left|YB\right|=\left|CY\right|+\left|YB\right|\ge \left|CB\right|$

Ostatnia nierówność wynika z nierówności trójkąta. 
Równość zachodzi, jeżeli punkt $Y$ leży na odcinku $CB$.

Zatem szukanym punktem na brzegu rzeki jest punkt przecięcia prostej $CB$ z „górnym” brzegiem rzeki – punkt $Z$. 
W tym miejscu należy wybudować most.

Punkt $P$ leży wewnątrz trójkąta równobocznego $ABC$ o boku długości $1$. Proste $AP$, $BP$, $CP$ przecinają odcinki $BC$, $CA$, $AB$ odpowiednio w punktach $D$, $E$, $F$ (rysunek).

Zastanówmy się jakie jest ograniczenie górne sumy: $\left|PD\right|+\left|PE\right|+\left|PF\right|$

R1NvXHbokjNCo

Na ilustracji przedstawiono trójkąt równoboczny $ABC$, o podstawie $AB$. Wewnątrz trójkąta zaznaczono punkt P. Zaznaczono punkt E leżący na boku $AC$, punkt D leżący na boku $BC$, punkt F leżący na boku $AB$. Linią przerywaną połączono punkt P z wierzchołkami A, B, C, trójkąta.

Rozwiązanie

Prowadzimy proste równoległe do boków trójkąta przechodzące przez punkt $P$:

RzjMJTwQAAVGF

Na ilustracji przedstawiono trójkąt równoboczny $ABC$, o podstawie $AB$. Wewnątrz trójkąta zaznaczono punkt P. Zaznaczono punkt E leżący na boku $AC$, punkt D leżący na boku $BC$, punkt F leżący na boku $AB$. Linią przerywaną połączono punkt P z wierzchołkami A, B, C, trójkąta. Zaznaczono prostą $GH$, przechodzącą przez punkt P, równoległą do boku $AB$. Poprowadzono prostą $JL$, przechodzącą przez punkt P, równoległą do boku $BC$, oraz prostą $KI$, przechodzącą przez punkt P, równoległą do boku $AC$.

Analizując dokładnie powyższy rysunek zwrócimy uwagę na najważniejsze aspekty rozwiązania:

• powstają trzy równoległoboki: $AKPG$, $LBHP$, $JPIC$ i trzy trójkąty równoboczne: $KLP$, $PHI$, $GPJ$.

• odcinek leżący wewnątrz trójkąta równobocznego jest krótszy od jego boku.

Na podstawie powyższych obserwacji otrzymujemy:

$\left|PD\right|+\left|PE\right|+\left|PF\right|<\left|PH\right|+\left|PG\right|+\left|KL\right|=\left|AK\right|+\left|KL\right|+\left|LB\right|=\left|\mathrm{AB}\right|$.

Zatem ograniczenie górne naszej sumy jest równe $\left|AB\right|=1$.

odcinek łączący środki pewnych dwóch boków trójkąta

zdanie „jeżeli $p$, to $q$”, co zapisujemy $p\Rightarrow q$