Przeczytaj
Granica funkcji w punkcie jest zazwyczaj liczbą rzeczywistą, nazywamy taką granicę granicą właściwągranicą właściwą. Nie zawsze tak jest, czasami taka granica może być nieskończona, nazywamy ją wówczas granicą niewłaściwą.
Definicja granicy niewłaściwej w punkcie
Przypomnijmy sobie dwie, równoważne definicje granic niewłaściwych funkcji w punkcie, według Heinego i Cauchy’ego.
Mówimy, że funkcja ma w punkcie granicę niewłaściwą równą , gdy poza samym punktem pewne jego otoczenie należy do dziedziny tej funkcji, oraz dla dowolnego ciągu argumentów z dziedziny, dążącego do , wartości dążą do .
Mówimy, że funkcja ma w punkcie granicę niewłaściwą równą , gdy poza samym punktem pewne jego otoczenie należy do dziedziny tej funkcji, oraz dla dowolnie dużej wartości dodatniej liczby istnieje taka liczba dodatnia , że dla wszystkich argumentów z dziedziny pomiędzy i wartości są większe od .
Symbolicznie zapisujemy to jako:
Podobnie definiujemy granicę niewłaściwą równą .
Sprawdzimy, używając definicji Heinego, czy funkcja , , ma w punkcie granicę niewłaściwągranicę niewłaściwą.
Rozwiązanie
Weźmy dowolny ciąg argumentów , dążący do zera. Wówczas wiemy, że ciąg kwadratów tych argumentów, , również dąży do zera, przyjmując tylko wartości dodatnie. Zatem ciąg przeciwieństw odwrotności kwadratów, , dąży do , czyli granicą funkcji w jest ,
.
Sprawdzimy, używając definicji Cauchy’ego, czy funkcja , , ma w punkcie granicę niewłaściwą.
Rozwiązanie
Weźmy dowolnie dużą liczbę dodatnią . Jeżeli zdefiniujemy liczbę dodatnią równą odwrotności pierwiastka z , czyli , to wówczas dla wszystkich niezerowych wartości większych od i mniejszych od wartości funkcji są mniejsze od , i tym samym granicą funkcji w jest .
Możemy sprawdzić empirycznie, jak wygląda znajdowanie wartości w zależności od wartości na przykładzie funkcji , .
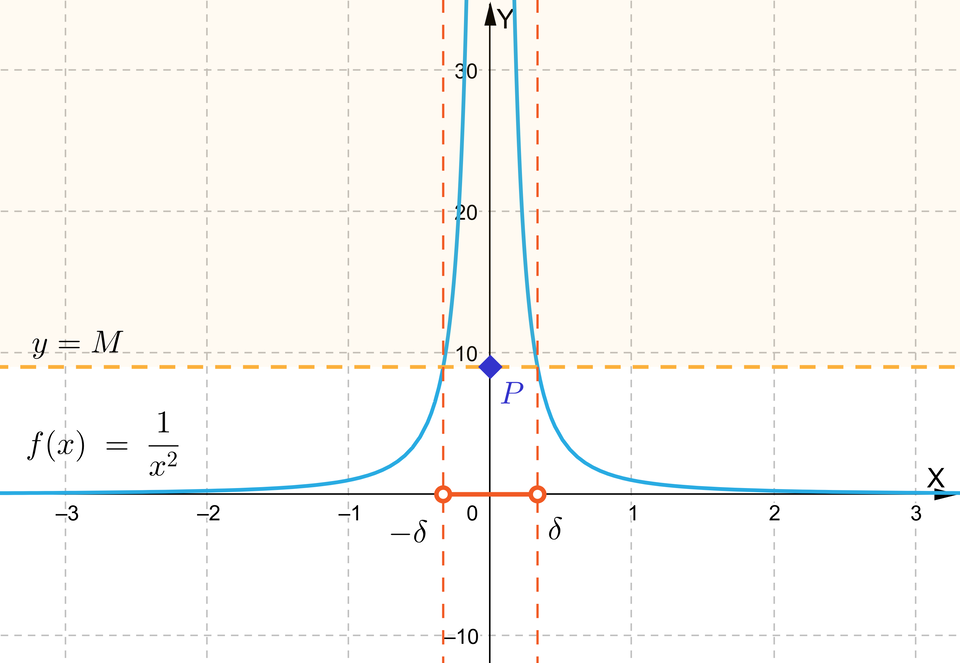
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D13DuFZB8
Jak widać, im większa wartość , tym mniejsza jest wartość – węższy jest zakres argumentów, dla których wartości funkcji są powyżej zadanej linii – ale za każdym razem można taką wartość znaleźć.
Znajdowanie granic niewłaściwych
Jeżeli funkcja jest ciągła w danym punkcie, to z definicji ciągłości wiemy, że jej granice jednostronne są równe wartości funkcji w tym punkcie. Ponieważ funkcje nie mogą mieć wartości nieskończonych, tym samym w punkcie, w którym funkcja jest ciągła, nie możemy nigdy otrzymać granicy niewłaściwej.
Sprawdzimy, czy funkcja może mieć w którymś punkcie granicę niewłaściwą.
Rozwiązanie
Nie może, bo jest funkcją ciągłą.
Jeżeli funkcja nie jest ciągła w punkcie, to wciąż nie musi mieć granicy niewłaściwej, może nawet mieć granicę skończoną.
Sprawdzimy, czy funkcja
może mieć w którymś punkcie granicę niewłaściwą.
Rozwiązanie
Dla żadnego punktu poza nie może, bo jest funkcją ciągłą. W punkcie nie jest ciągła, ale również nie posiada granicy niewłaściwej, bo posiada granicę skończoną, równą .
Dla posiadania granicy niewłaściwej funkcja nie może być w danym punkcie ciągła, ani nie może posiadać tam granicy skończonej. Łatwo to zweryfikować, gdy funkcja jest zadana prostym wzorem, lub gdy zna się wykres funkcji. Jeżeli funkcja jest zadana trudnym wzorem, na przykład jest funkcją wymierną, trzeba dokonać niezbędnych obliczeń.
Zbadamy, czy funkcja
ma w punktach i granice niewłaściwe.
Rozwiązanie
Zachowanie w punkcie sprawdzamy, podstawiając do wzoru funkcji, otrzymując
,
czyli funkcja w punkcie posiada granicę skończoną równą .
Dla punktu mamy:
,
i
.
Zatem funkcja w punkcie posiada jednostronne granice niewłaściwe.
Słownik
granica funkcji w punkcie, która jest liczbą rzeczywistą
granica funkcji w punkcie, która jest nieskończona ( lub )