Przeczytaj

R1DFNZviY4nIK

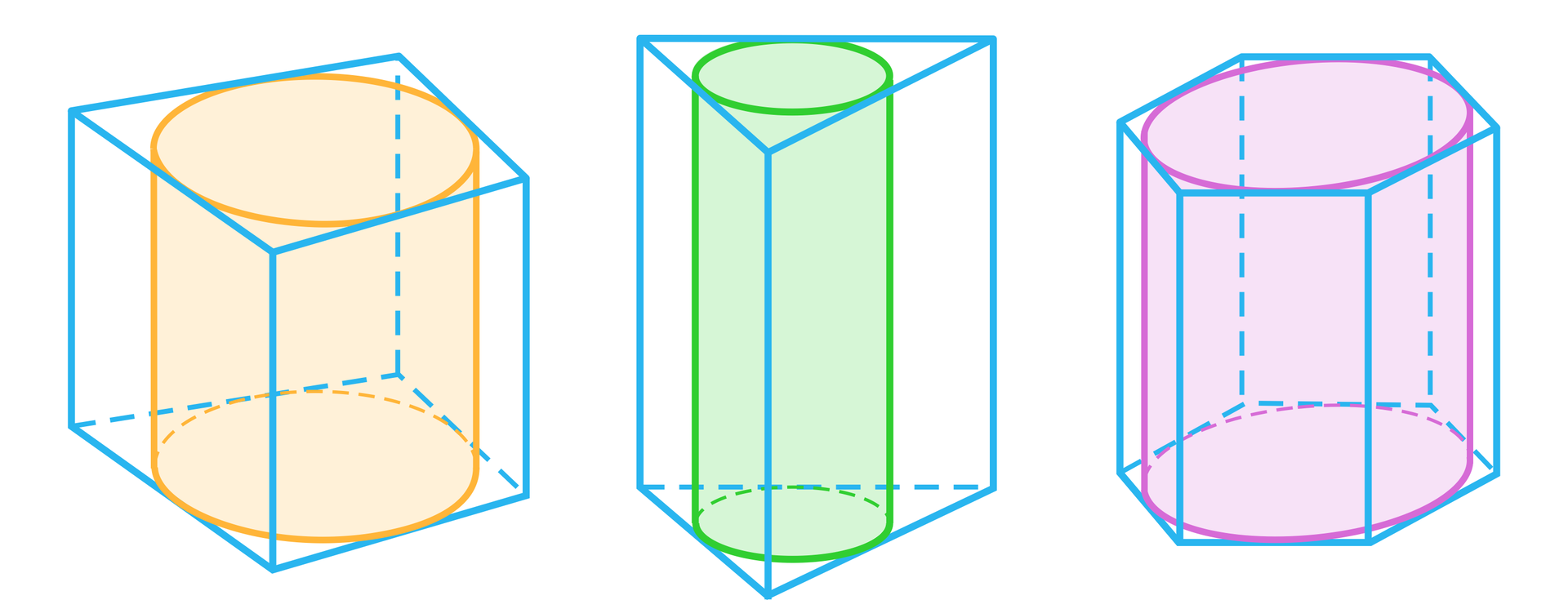
Na ilustracji przedstawiono trzy różne graniastosłupy opisane na walcu. Kolejno od lewej graniastosłup prosty czworokątny, graniastosłup prosty trójkątny oraz graniastosłup prosty sześciokątny.

Graniastosłup jest opisany na walcugraniastosłup opisany na walcuGraniastosłup jest opisany na walcu, jeśli jego podstawy są wielokątami opisanymi na podstawach walca. Zauważmy, że wysokość graniastosłupa jest taka sama jak wysokość walca.

Podstawą graniastosłupa musi być wielokąt, w który można wpisać okrąg. To kryterium spełniają wszystkie wielokąty foremne, a zatem w każdy graniastosłup prawidłowygraniastosłup prawidłowygraniastosłup prawidłowy można wpisać walec.

Przypomnimy najpierw podstawowe wzory:

długość promienia okręgu wpisanego w trójkąt prostokątny o przeciwprostokątnej długości $c$ i przyprostokątnych długości $a$ i $b$ wyraża się wzorem $r = \frac{a + b - c}{2}$
długość promienia okręgu wpisanego trójkąt równoboczny o boku długości $a$ , wyraża się wzorem $r = \frac{a \sqrt{3}}{6}$
długość promienia okręgu wpisanego w dowolny trójkąt wyraża się wzorem $r = \frac{P_{Δ}}{p}$ , gdzie $P_{Δ}$ - pole trójkąta, $p$ – połowa obwodu tego trójkąta
długość promienia okręgu wpisanego w czworokąt o bokach długości $a$ , $b$ , $c$ , $d$ wyraża się wzorem $r = \frac{2 P}{a + b + c + d}$ , gdzie $P$ oznacza pole czworokąta
pole kwadratu o przekątnej długości $d$ wyraża się wzorem $P = \frac{d^{2}}{2}$
pole trójkąta o bokach długości $a$ , $b$ i $c$ wyraża się wzorem $P_{Δ} = \sqrt{p (p - a) (p - b) (p - c)}$ , gdzie $p$ jest połową obwodu trójkąta
objętość walca o promieniu długości $r$ i wysokości długości $H$ wyraża się wzorem $V = π r^{2} H$
pole powierzchni walca o promieniu długości $r$ i wysokości długości $H$ wyraża się wzorem $P = 2 π r^{2} + 2 π r \cdot H$

Przykład 1

Rozważmy graniastosłup prawidłowygraniastosłup prawidłowygraniastosłup prawidłowy sześciokątny, którego wszystkie krawędzie mają długość $a$ . Wykażemy, że stosunek objętości walca opisanego na tym graniastosłupie do objętości walca wpisanego w ten graniastosłup jest równy $\frac{4}{3}$ .

Rozwiązanie:

Wykonajmy odpowiedni rysunek.

R1NiOJfvNv1Wz

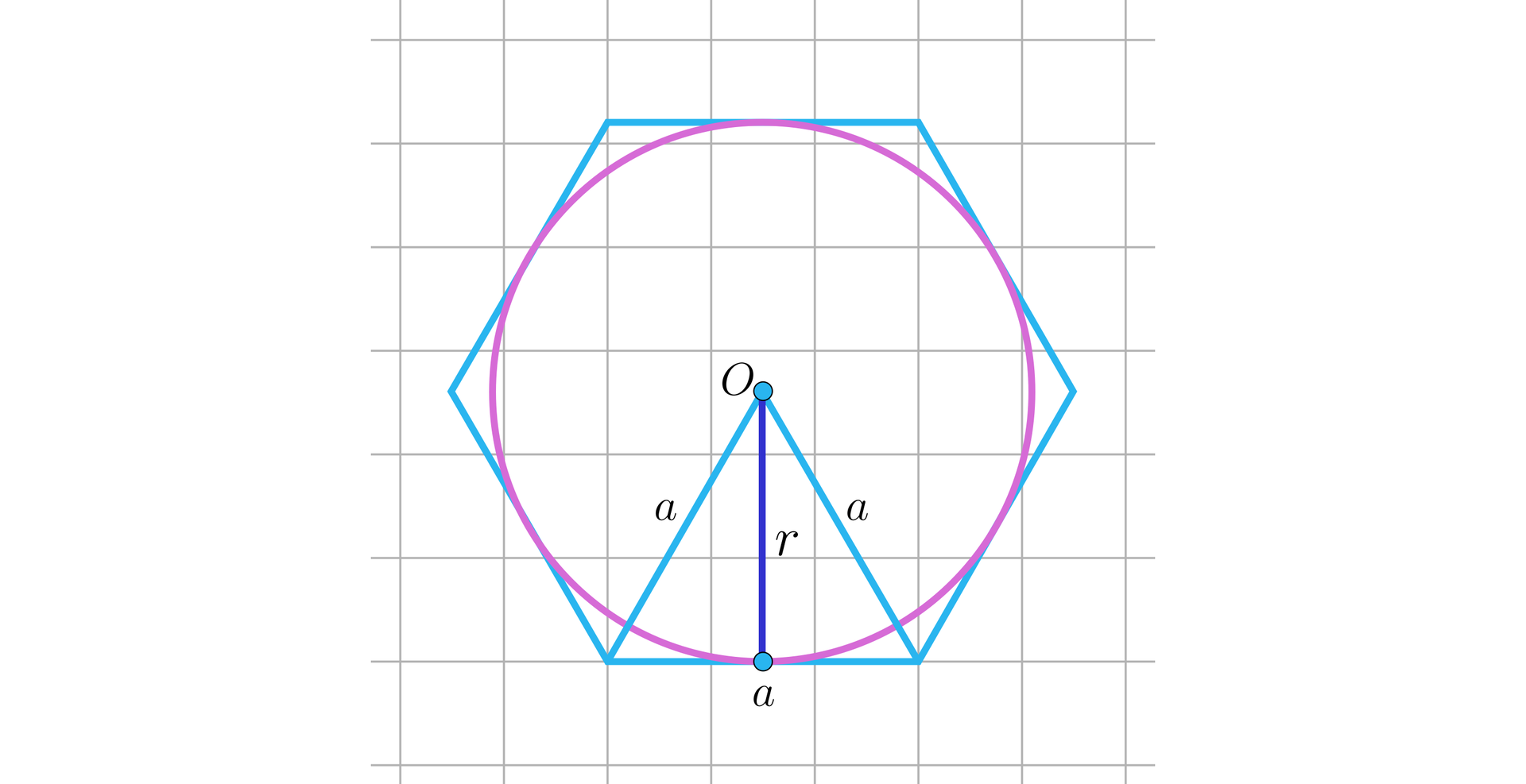
Ilustracja przedstawia pole w kratkę. Na płaszczyźnie narysowano sześciokąt, w który wpisano okrąg o środku w punkcie O. Długość boku sześciokąta oznaczono literą a. Zaznaczono dwa odcinki łączące punkt O z wierzchołkami tego samego boku, których długość wynosi a. Z punktu O poprowadzono także odcinek prostopadły do boku sześciokąta a zarazem styczny do okręgu.

Promień podstawy walca wpisanego w ten graniastosłup jest wysokością w trójkącie równobocznym o boku długości $a$ . Zatem $r = \frac{a \sqrt{3}}{2}$ .

Stąd objętość walca wpisanego w ten graniastosłup jest równa:

$V_{w} = π \cdot r^{2} \cdot a = π \cdot {(\frac{a \sqrt{3}}{2})}^{2} \cdot a = \frac{3 π a^{3}}{4}$ .

Promień podstawy walca opisanego na tym graniastosłupie jest równy długości krawędzi podstawy czyli $r = a$ .

A zatem objętość walca opisanego na tym graniastosłupie jest równa $V_{0} = π \cdot a^{2} \cdot a = π a^{3}$ .

Otrzymujemy:

$\frac{V_{o}}{V_{w}} = π a^{3} \cdot \frac{4}{3 π a^{3}} = \frac{4}{3}$ .

Przykład 2

Z kawałka drewna w kształcie graniastosłupa prawidłowego trójkątnego o wysokości trzy razy dłuższej niż krawędź podstawy i objętości $750 \sqrt{3} {dm}^{3}$ mamy wykonać klocek. Klocek ten ma mieć kształt walca wpisanego w graniastosłup (przy czym podstawy walca są wpisane w podstawy graniastosłupa). Oblicz objętość jaką zajmują odpady. Wartość podaj z dokładnością do $1 {dm}^{3}$ . Przyjmij $π \approx 3, 14$ .

Rozwiązanie:

Z treści zadania wynika, że $h = 3 a$ .

Stąd $V = \frac{a^{2} \sqrt{3}}{4} \cdot h = \frac{3 a^{3} \sqrt{3}}{4}$ .

A więc otrzymujemy równanie

$\frac{3 a^{3} \sqrt{3}}{4} = 750 \sqrt{3}$

$a^{3} = 1000$

$a = 10 [dm]$

Stąd $h = 30 [dm]$ .

Długość promienia okręgu wpisanego w trójkąt równoboczny o boku $a$ jest równa $r = \frac{a \sqrt{3}}{6} = \frac{5 \sqrt{3}}{3} [dm]$ .

Objętość walca jest równa $V_{w} = π r^{2} h = π {(\frac{5 \sqrt{3}}{3})}^{2} \cdot 30 = 250 π [{dm}^{3}]$ .

Objętość odpadów to różnica między objętością walca, a objętością graniastosłupa, czyli:

$(750 \sqrt{3} - 250 π) {dm}^{3} \approx 1299 {dm}^{3} - 785 {dm}^{3} = 514 {dm}^{3}$ .

Przykład 3

Podstawą graniastosłupa prostegograniastosłup prostygraniastosłupa prostego jest trójkąt o bokach długości $4$ , $5$ i $7$ . Wysokość tego graniastosłupa jest równa $H = 16$ . Obliczymy pole przekroju osiowego walca wpisanego w ten graniastosłup.

Rozwiązanie:

Ponieważ podstawą tego graniastosłupa jest trójkąt o bokach długości $a = 4$ , $b = 5$ i $c = 7$ , który nie jest trójkątem prostokątnym ponieważ $7^{2} \neq 4^{2} + 5^{2}$ , jego pole policzymy ze wzoru Herona:

$p = \frac{4 + 5 + 7}{2} = 8$

$P_{Δ} = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{8 \cdot 4 \cdot 3 \cdot 1} = 4 \sqrt{6}$

Obliczymy długość promienia okręgu wpisanego w ten trójkąt:

Otrzymujemy $r = \frac{P_{Δ}}{p} = \frac{4 \sqrt{6}}{8} = \frac{\sqrt{6}}{2}$ .

Przekrój osiowy walca jest prostokątem o bokach długości $2 r$ i $H$ , czyli jego pole jest równe $P = 2 r H = 2 \cdot \frac{\sqrt{6}}{2} \cdot 16 = 16 \sqrt{6}$ .

Przykład 4

Przekątna przekroju osiowego walca, równa $d$ nachylona jest do płaszczyzny podstawy walca pod kątem $α$ . Wykażemy, że objętość graniastosłupa prawidłowego czworokątnego opisanego na tym walcu jest równa $\frac{1}{2} d^{3} \sin 2 α \cdot \cos α$ .

Rozwiązanie:

W rozwiązaniu posłużymy się przekrojem osiowym walca, który jest prostokątem o bokach $H$ i $2 r$ .

R1WJfaWtlKF38

Ilustracja przedstawia pole w kratkę. Na płaszczyźnie narysowano prostokąt. Długość dłuższego boku oznaczono wielką literą H, natomiast długość krótszego boku oznaczono 2r. Zaznaczono przekątną, której długość oznaczono literą d. Kąt nachylenia przekątnej do krótszego boku prostokątna oznaczono alfa.

Z definicji funkcji trygonometrycznych w trójkącie prostokątnym otrzymujemy:

$\sin α = \frac{H}{d}$

$H = d \sin α$

oraz

$\cos α = \frac{2 r}{d}$

$2 r = d \cos α$

Ponieważ średnica okręgu wpisanego w kwadrat jest równa długości jego boku, objętość graniastosłupa możemy obliczyć następująco:

$V = {(2 r)}^{2} \cdot H = d^{2} \cos^{2} α \cdot d \sin α = d^{3} \sin α \cos^{2} α =$ $= \frac{1}{2} d^{3} 2 \sin α \cdot \cos^{2} α = \frac{1}{2} d^{3} \sin 2 α \cdot \cos α$

Słownik

graniastosłup opisany na walcu

graniastosłup, którego podstawy są wielokątami opisanymi na podstawach walca

graniastosłup prawidłowy

graniastosłup prosty, którego postawami są wielokąty foremne

graniastosłup prosty

graniastosłup, którego ściany boczne są prostokątami

Wprowadzenie

Prezentacja multimedialna

Słownik