Przeczytaj

Ekstrema, czyli maksima i minima, to pewne wartości przyjmowane przez rozpatrywaną funkcję. Intuicyjnie łatwo zrozumieć, czym jest minimalna i maksymalna wartość danej funkcji, jednak sformalizowanie tego pojęcia nie jest aż tak proste.

Funkcja kwadratowa posiada dokładnie jedno ekstremum w punkcie, który jest wierzchołkiem wykresu funkcji kwadratowej. Oznacza to, że nie musimy szukać ekstremum lokalnego, możemy od razu przejść do wyznaczania ekstremum globalnego funkcji.

Maksimum, minimum globalne

Definicja: Maksimum, minimum globalne

Niech dana będzie funkcja rzeczywista $f : X ⟶ ℝ$ . Powiemy, że funkcja $f$ osiąga maksimum globalne w punkcie $x_{0} \in X$ , jeżeli dla dowolnego punktu $x \in X$ spełniona jest nierówność

f (x_{0}) ⩾ f (x)

Analogicznie, powiemy, że funkcja $f$ osiąga minimum globalne w punkcie $x_{0} \in X$ , jeżeli dla dowolnego punktu $x \in X$ zachodzi nierówność

f (x_{0}) ⩽ f (x)

Liczbę $f (x_{0})$ nazywamy wówczas (odpowiednio) największą lub najmniejszą wartością funkcji $f$ w zbiorze $X$ .

Ekstrema pojawiają się w wielu problemach współczesnej nauki. W niektórych przypadkach wyznaczenie minimalnej i maksymalnej wartości dla danej funkcji jest zadaniem trudnym. W przypadku funkcji kwadratowej jest jednak inaczej, co wynika z kształtu jej wykresu tj. paraboli. Przypatrzmy się poniższym wykresom.

Ra3Ij24tfCuYw

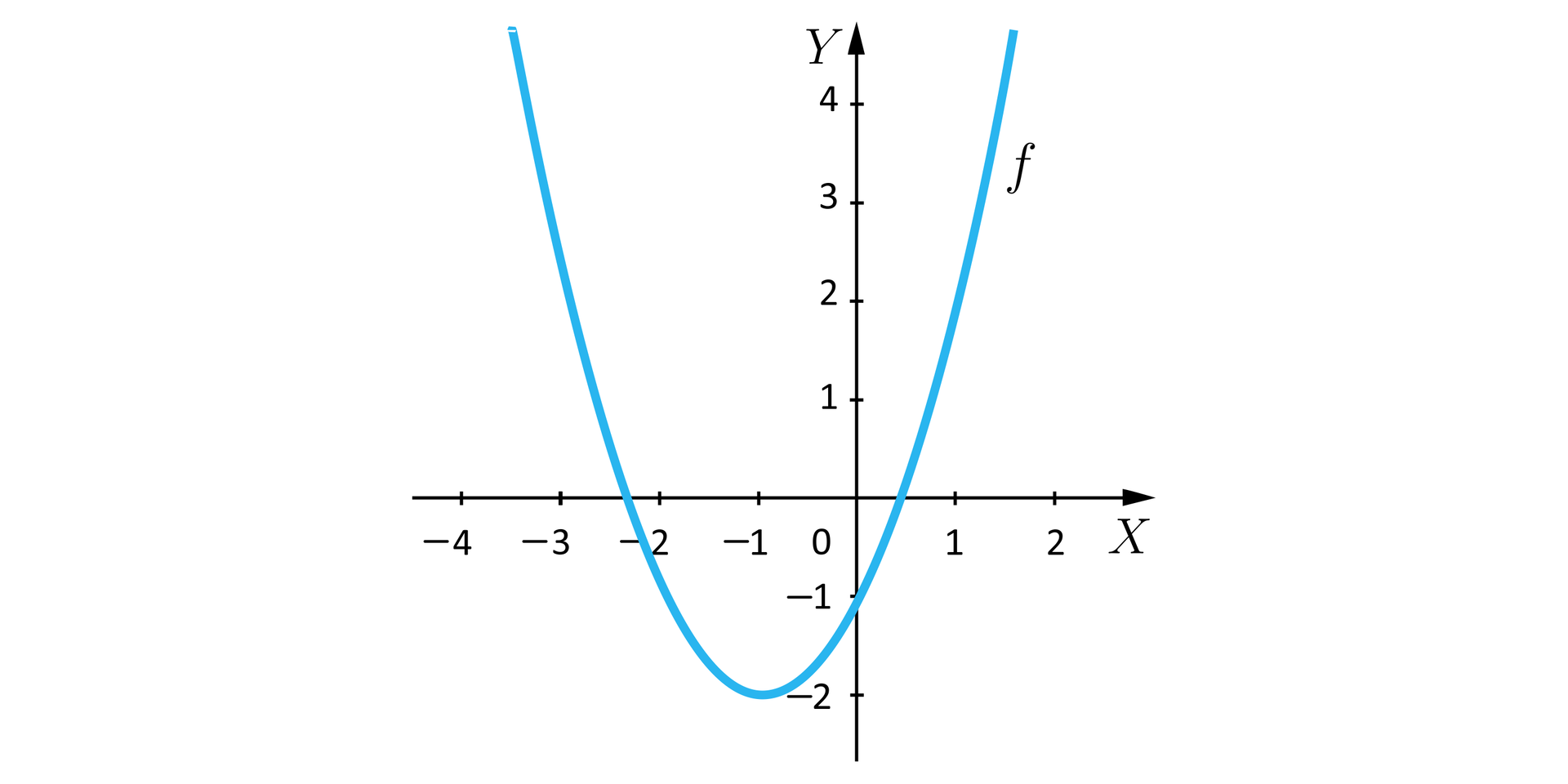
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus czterech do dwóch, oraz z pionową osią Y od minus dwóch do czterech. Na płaszczyźnie narysowano wykres funkcji fx. Wykresem funkcji jest parabola o wierzchołku w punkcie -2;-3 i ramionach skierowanych w górę.

RjDNJz7f8ar68

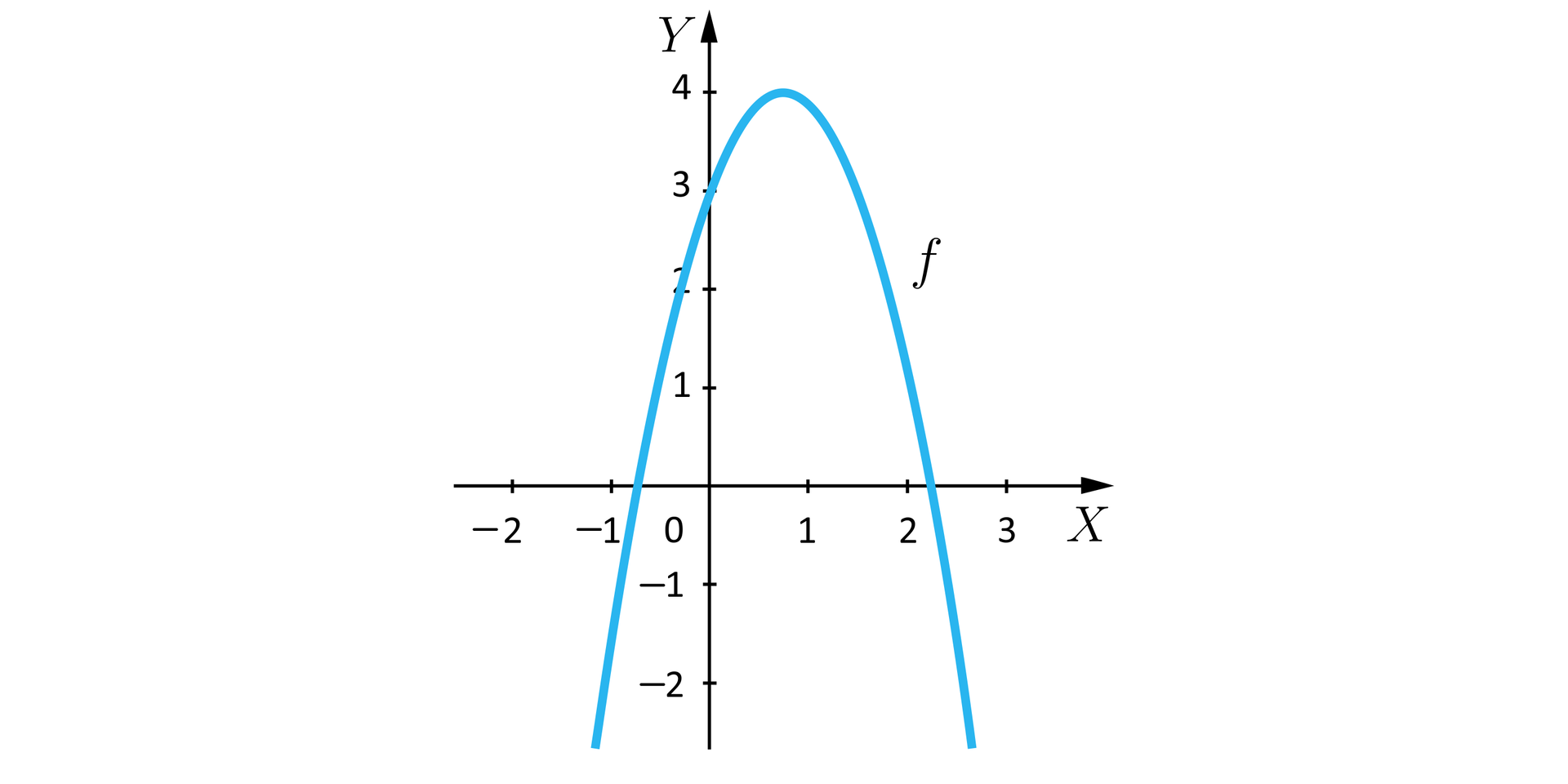
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus dwóch do trzech, oraz z pionową osią Y od minus dwóch do czterech. Na płaszczyźnie narysowano wykres funkcji fx. Wykresem funkcji jest parabola o wierzchołku w punkcie 1;4 i ramionach skierowanych do dołu.

Każda parabola (opisywana równaniem $y = a x^{2} + b x + c$ ) ma dokładnie jeden wierzchołek. Wierzchołek ten odpowiada największej lub najmniejszej wartości przyjmowanej przez zadaną funkcję kwadratową – charakter tego ekstremum zależy od znaku współczynnika $a$ przy wyrażeniu $x^{2}$ .

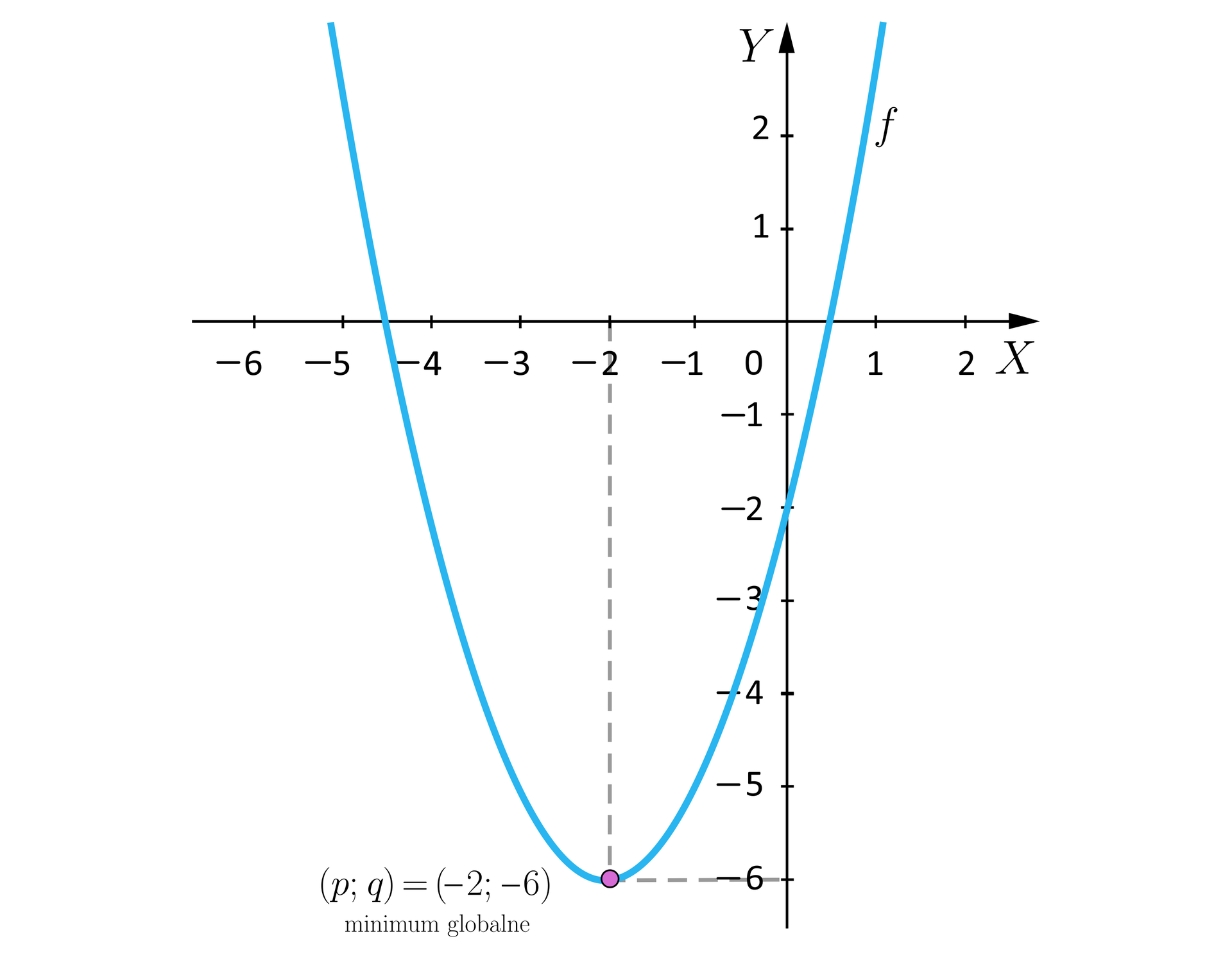
Jak obserwujemy na wykresach, skierowane ku górze ramiona paraboli (czyli dodatni współczynnik $a$ ) przekładają się na istnienie minimum globalnego funkcji kwadratowej. W takiej sytuacji funkcja nie jest ograniczona z góry, więc nie możemy mówić o jej maksimum globalnym.

Z kolei w przypadku, gdy $a$ ma wartość mniejszą od zera, minimum globalne nie istnieje, ale za to parabola posiada maksimum globalne. Możemy więc sformułować następującą obserwację.

Ważne!

Zwróćmy teraz uwagę na ważną obserwację.
Funkcja kwadratowa $f : ℝ ⟶ ℝ$ zadana wzorem $f (x) = a x^{2} + b x + c$ ma dokładnie jedno ekstremum globalne. Jest to minimum, w sytuacji gdy $a > 0$ , zaś maksimum, gdy $a < 0$ .
Współrzędne takiego ekstremum można wyznaczyć z postaci kanonicznej funkcji kwadratowejpostać kanoniczna funkcji kwadratowejkanonicznej funkcji kwadratowej, czyli dla $f (x) = a {(x - p)}^{2} + q$ wierzchołek paraboli opisywanej przez wzór funkcji $f$ znajduje się w punkcie o współrzędnych $(p, q)$ . Oznacza to, że funkcja kwadratowa ma ekstremum globalne w punkcie $p$ o wartości $q$ .

Przykład 1

Wyznaczymy ekstremum globalne funkcji $f (x) = 2 \cdot {(x - 1)}^{2} - 3$ .

Rozwiązanie

Ponieważ $a = 2 > 0$ , to funkcja ma minimum globalne w punkcie $p = 1$ , wynoszące $q = f (p) = - 3$ .

R1Fjnvkz7UJA4

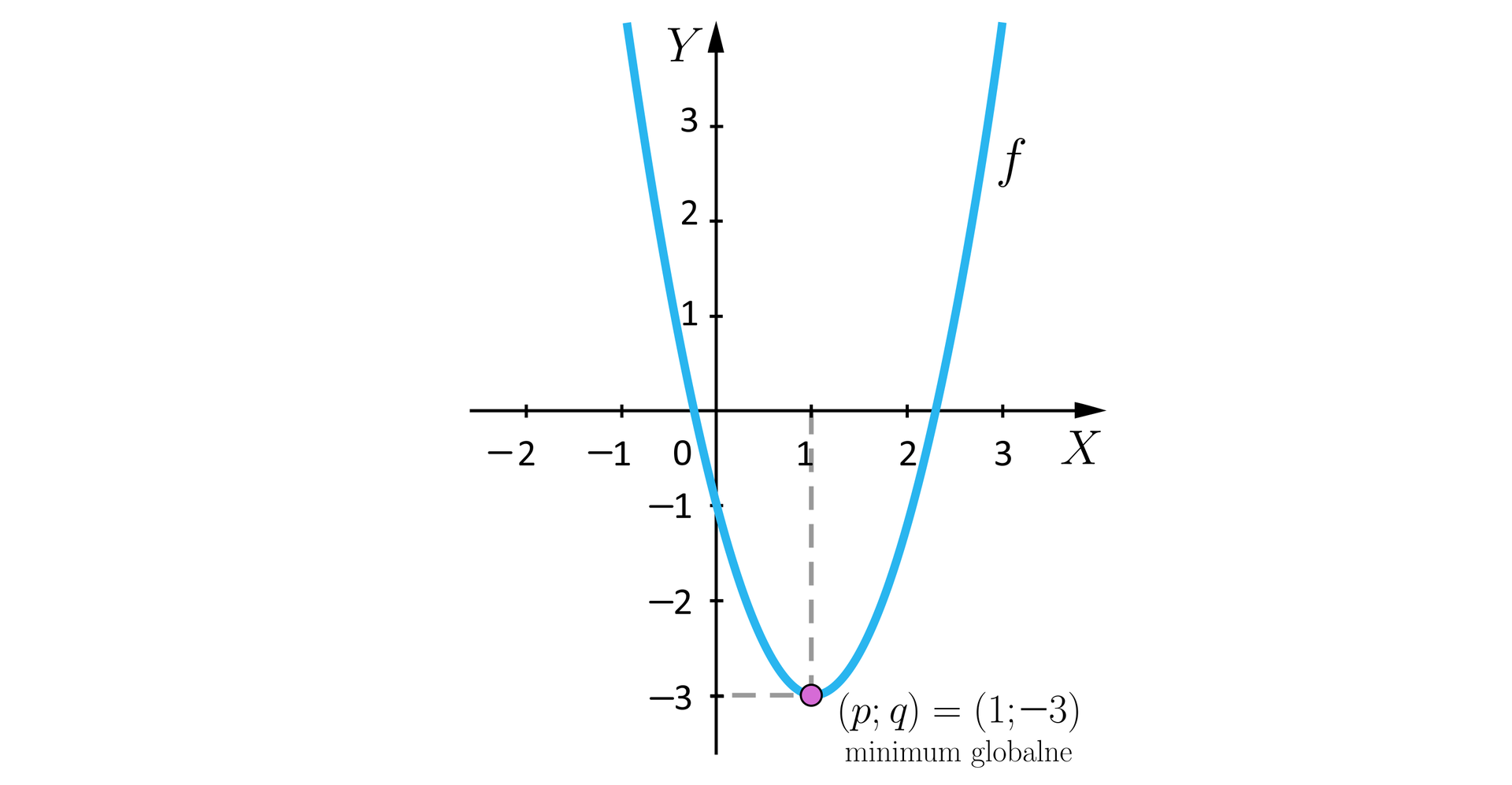
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus dwóch do trzech i pionową osią y od minus trzech do trzech. W układzie zaznaczono wykres funkcji f o kształcie paraboli, której ramiona są skierowane do góry. Wierzchołek paraboli znajduje się w punkcie nawias p średnik q zamknięcie nawiasu, czyli w punkcie nawias jeden średnik minus trzy zamknięcie nawiasu.

Jeżeli wzór funkcji kwadratowej jest zapisany w postaci iloczynowejpostać iloczynowa funkcji kwadratowejpostaci iloczynowej, to argument, w którym znajduje się minimum (lub maksimum) globalne, jest średnią arytmetyczną miejsc zerowych tej funkcji.

Ekstremum globalne

Twierdzenie: Ekstremum globalne

Niech dana będzie funkcja kwadratowa $f : ℝ ⟶ ℝ$ określona wzorem w postaci iloczynowej $f (x) = a (x - x_{1}) (x - x_{2})$ . Wówczas funkcja $f$ posiada ekstremum globalne w punkcie

p = \frac{x_{1} + x_{2}}{2}

Przykład 2

Wyznaczymy ekstremum globalne funkcji kwadratowej: $f (x) = - 2 \cdot (x - 2) (x - 4)$ .

Rozwiązanie

Ponieważ $a = - 2 < 0$ , to funkcja ma maksimum globalne w punkcie $p = \frac{4 + 2}{2} = 3$ . Największa wartość przyjmowana przez tę funkcję wynosi więc $q = f (3) = - 2 \cdot (3 - 2) (3 - 4) = - 2 \cdot 1 \cdot (- 1) = 2$ .

R1DNMGdCXHHni

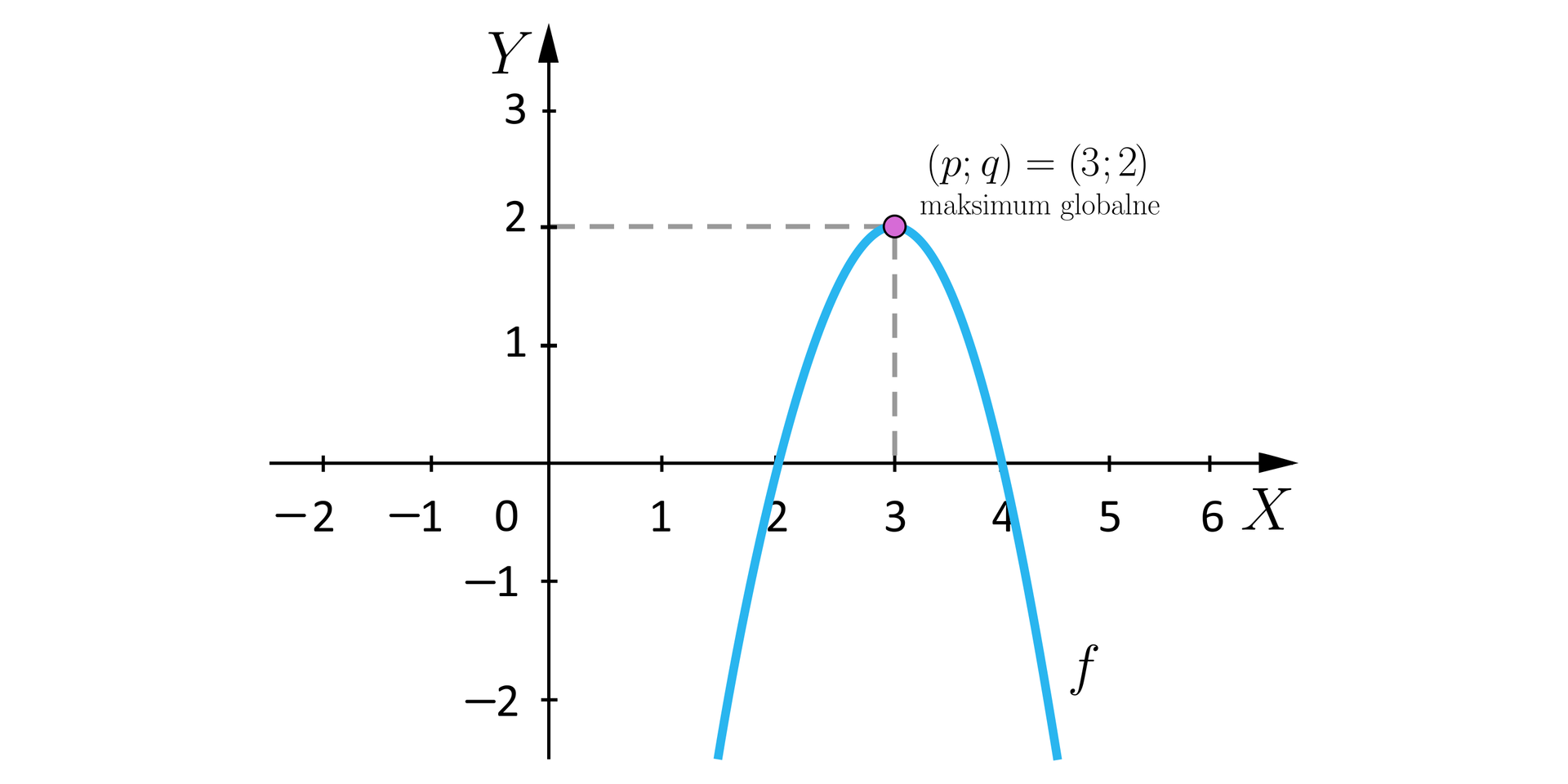
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus dwóch do sześciu i pionową osią y od minus dwóch do trzech. W układzie zaznaczono wykres funkcji f o kształcie paraboli, której ramiona są skierowane do dołu. Wierzchołek paraboli znajduje się w punkcie nawias p średnik q zamknięcie nawiasu, czyli w punkcie nawias trzy średnik dwa zamknięcie nawiasu.

W przypadku gdy funkcja kwadratowa jest podana w postaci ogólnej, zagadnienie znajdowania ekstremum funkcji kwadratowej sprowadza się do wyznaczenia wierzchołka opisywanej przez nią paraboli.

Wierzchołek paraboli

Twierdzenie: Wierzchołek paraboli

Niech dana będzie funkcja kwadratowa $f : ℝ ⟶ ℝ$ w postaci ogólnej $f (x) = a x^{2} + b x + c$ .

Wówczas wierzchołek paraboli opisanej przez funkcję $f$ znajduje się w punkcie $(p, q)$ , gdzie $p$ i $q$ opisane są wzorami

p = \frac{- b}{2 a}

q = \frac{- ∆}{4 a} = \frac{- b^{2} + 4 a c}{4 a}

Przykład 3

Wyznaczymy ekstremum globalne funkcji $f (x) = x^{2} + 4 x - 2$ .

Rozwiązanie

Ponieważ $a = 1 > 0$ , to funkcja ma minimum lokalne w punkcie $p = - \frac{4}{2 \cdot 1} = - 2$ .

Najmniejszą wartość osiąganą przez tę funkcję możemy obliczyć następująco:

$q = f (- 2) = {(- 2)}^{2} + 4 \cdot (- 2) - 2 = 4 - 8 - 2 = - 6$

lub z podanego wyżej wzoru

$q = \frac{- 4^{2} + 4 \cdot 1 \cdot (- 2)}{4 \cdot 1} = \frac{- 16 - 8}{4} = \frac{- 24}{4} = - 6$ .

R104OLUEYoqx0

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus sześciu do dwóch i pionową osią y od minus sześciu do dwóch. W układzie zaznaczono wykres funkcji f o kształcie paraboli, której ramiona są skierowane do góry. Wierzchołek paraboli znajduje się w punkcie nawias p średnik q zamknięcie nawiasu, czyli w punkcie nawias minus dwa średnik minus sześć zamknięcie nawiasu.

Przykład 4

Wyznaczymy dla jakiej wartości parametru $m \in ℝ$ funkcja $f$ określona wzorem $f (x) = m x^{2} - (m + 2) x + 5$ osiąga ekstremum dla $x = 1$ . Czy jest to maksimum czy minimum?

Rozwiązanie

Zauważmy, że funkcja $f$ ma ekstremum lokalne w punkcie $x = 1$ oznacza to, że

$1 = \frac{m + 2}{2 m}$

$2 m = m + 2$

$m = 2$ .

Wzór szukanej funkcji, to $f (x) = 2 x^{2} - 4 x + 5$ . Ponieważ $a = 2 > 0$ , to funkcja w punkcie $x = 1$ osiąga minimum lokalne.

Najmniejszą wartość osiąganą przez tą funkcję możemy obliczyć następująco:

$f (1) = 2 - 4 + 5 = 3$ .

Do czego można wykorzystać umiejętność wyznaczania ekstremów funkcji kwadratowej?

Wyjaśniamy to na praktycznym przykładzie.

Przykład 5

Wyznaczymy maksymalne pole prostokąta, którego obwód wynosi $48 cm$ . Podamy też długości boków, przy których osiągane jest to maksymalne pole.

Rozwiązanie

Przypomnijmy wzory na pole i obwód prostokąta o bokach, których długości oznaczymy przez $x$ i $y$ .

$P = x \cdot y$

$L = 2 x + 2 y$

Podstawiamy znaną nam wartość obwodu do wzoru.

$48 = 2 x + 2 y$

Dzielimy obie strony równości przez $2$ .

$24 = x + y$

Przekształcamy równość, wyznaczając z niej wartość $y$ .

$y = 24 - x$ , $x \in (0, 24)$

Podstawiamy tak przedstawioną długość boku $y$ do wzoru na pole prostokąta.

$P = x \cdot (24 - x)$ , $x \in (0, 24)$

Wartość pola rozważanego prostokąta, w zależności od długości boku $x$ , jest wyrażona przez następującą funkcję kwadratową:

$P = - x^{2} + 24 x$ , $x \in (0, 24)$

Ponieważ $a = - 1 < 0$ , to funkcja w wierzchołku osiąga największą wartość.

Wypiszemy współczynniki powyższej funkcji kwadratowej.

$a = - 1$ , $b = 24$ , $c = 0$

Maksymalną wartość pola prostokąta wyznaczamy, korzystając ze wzoru na współrzędną $q$ wierzchołka paraboli.

$q = \frac{- ∆}{4 a} = \frac{- 24^{2} + 4 \cdot (- 1) \cdot 0}{4 \cdot (- 1)} = \frac{- 576}{- 4} = 144$

Uzyskany wynik to $144 {cm}^{2}$ . Jest to największe pole, jakie może mieć prostokąt o obwodzie $48 cm$ .

Obliczymy teraz długości boków prostokąta o maksymalnym polu. W tym celu wykorzystujemy wzór na współrzędną $p$ punktu opisującego wierzchołek paraboli.

$p = \frac{- b}{2 a} = \frac{- 24}{2 \cdot (- 1)} = 12$

Zatem $x = 12 cm$ i $x \in (0, 24)$ jest długością boku, dla której obliczone wcześniej maksymalne pole jest osiągane. Długość boku $y$ wyliczamy z zależności:

$y = 24 - x$

co daje:

$y = 12$

Wiedząc więc, że $x = y = 12 cm$ możemy stwierdzić, że maksymalne pole powierzchni dla prostokąta o obwodzie $48 cm$ wynosi $144 {cm}^{2}$ i jest osiągane przez kwadrat o boku $12 cm$ .

Przykład 6

Na bokach prostokąta o obwodzie $20 cm$ oparto cztery trójkąty równoboczne. Wyznaczymy jakie powinny być długości boków trójkąta, aby pole całej figury złożonej z prostokąta i trójkątów było najmniejsze.

Rozwiązanie

Korzystając z poprzedniego przykładu wiemy, że wzory na pole i obwód prostokąta o bokach, których długości oznaczymy przez $x$ i $y$ , to

$P = x \cdot y$ ,

$L = 2 x + 2 y$ .

Podstawiamy znaną nam wartość obwodu do wzoru.

$20 = 2 x + 2 y$

Dzielimy obie strony równości przez $2$ .

$10 = x + y$

Przekształcamy równość, wyznaczając z niej wartość $x$ .

$x = 10 - y$ , $y \in (0, 10)$ .

Podstawiamy tak przedstawioną długość boku $x$ do wzoru na pole trójkąta równobocznego.

Oznaczmy:

$P_{1}$ – pole trójkąta o boku $x$ ,

$P_{2}$ – pole trójkąta o boku $y$ .

$P_{1} = \frac{x^{2} \sqrt{3}}{4} = \frac{{(y - 10)}^{2} \sqrt{3}}{4}$ ,

$P_{2} = \frac{y^{2} \sqrt{3}}{4}$ .

Zatem pole całej figury będzie równe:

$P_{c} = (10 - y) y + 2 \cdot \frac{y^{2} \sqrt{3}}{4} + 2 \cdot \frac{{(y - 10)}^{2} \sqrt{3}}{4}$

$P_{c} = 10 y - y^{2} + \frac{1}{2} (y^{2} \sqrt{3} + {(y - 10)}^{2} \sqrt{3})$

$P_{c} = (\sqrt{3} - 1) y^{2} + (10 - 10 \sqrt{3}) y + 50 \sqrt{3}$ , $y \in (0, 10)$ .

Ponieważ $a = \sqrt{3} - 1 > 0$ , to funkcja w wierzchołku osiąga najmniejszą wartość.

Obliczymy długości boków prostokąta, tak aby otrzymana figura miała najmniejsze pole. W tym celu wykorzystujemy wzór na współrzędną $p$ punktu opisującego wierzchołek paraboli.

$p = \frac{- b}{2 a} = \frac{- (10 - 10 \sqrt{3})}{2 (\sqrt{3} - 1)} = \frac{5 \sqrt{3} - 5}{\sqrt{3} - 1} \cdot \frac{\sqrt{3} + 1}{\sqrt{3} + 1} = \frac{10}{2} = 5$

Zatem $y = 5 cm$ i $y \in (0, 10)$ jest długością boku, dla którego obliczone wcześniej minimalne pole jest osiągane. Długość boku $x$ wyliczamy z zależności:

$x = 10 - y$

co daje:

$x = 5$ .

Widzimy, że boki prostokąta, dla których pole całej figury złożonej z prostokąta i trójkątów było najmniejsze, mają długości: $x = y = 5 cm$ .

Słownik

wyróżnik wielomianu stopnia drugiego

liczba charakterystyczna dla funkcji kwadratowej oznaczana przez $∆$ ; przy zapisie funkcji w postaci:

$f (x) = a x^{2} + b x + c$ , to wyróżnik ten zadany jest wzorem $∆ = b^{2} - 4 a c$

postać iloczynowa funkcji kwadratowej

zapis wzoru funkcji kwadratowej w postaci iloczynu czynników liniowych; korzystanie z niego jest możliwe, gdy wyróżnik trójmianu kwadratowego jest nieujemny; dla takich funkcji zapis ten ma postać:

$f (x) = a \cdot (x - x_{1}) \cdot (x - x_{2})$ , gdy $∆ > 0$ , gdzie $x_{1}$ , $x_{2}$ są miejscami zerowymi funkcji $f$

$f (x) = a \cdot {(x - x_{0})}^{2}$ , gdy $∆ = 0$ , wówczas $x_{0}$ jest miejscem zerowym funkcji $f$

postać kanoniczna funkcji kwadratowej

zapis wzoru funkcji kwadratowej, w którym wyeksponowany jest wierzchołek paraboli będącej jej wykresem; funkcja przedstawiona w tej postaci opisana jest wzorem:

$f (x) = a \cdot {(x - p)}^{2} + q$ , gdzie $(p, q)$ są współrzędnymi wierzchołka paraboli; w przeciwieństwie do postaci iloczynowej, postać kanoniczna istnieje zawsze, niezależnie od wartości wyróżnika trójmianu kwadratowegowyróżnik wielomianu stopnia drugiegowyróżnika trójmianu kwadratowego

Wprowadzenie

Symulacja interaktywna

Słownik