Symulacja interaktywna
Zmieniaj wartości współczynników funkcji kwadratowej opisanej równaniem . Obserwuj, które z parametrów wpływają na położenie ekstremum, a które jedynie modyfikują przyjmowaną w tym ekstremum wartość funkcji .
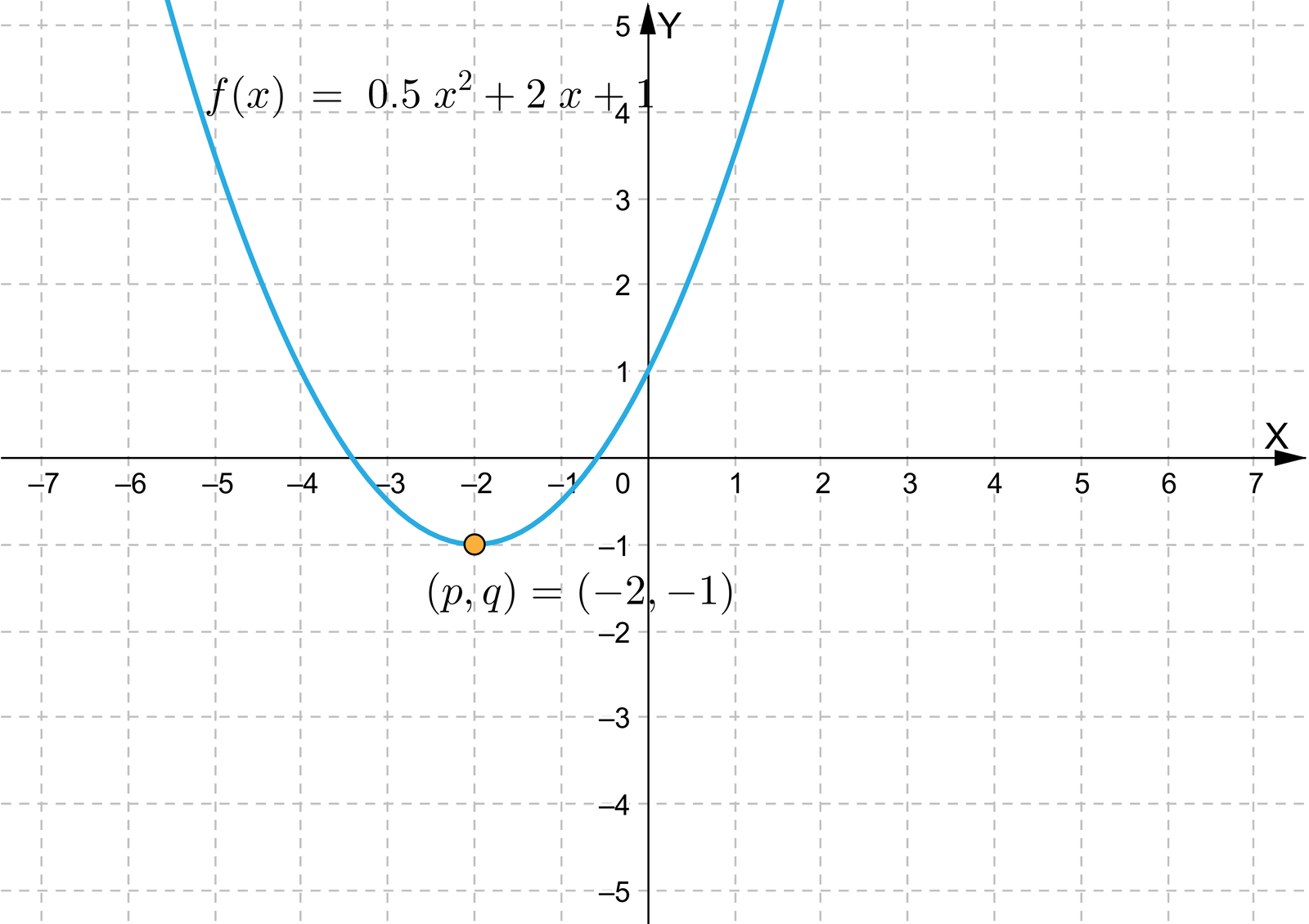
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/De5QdAPEN
Wykorzystaj symulację. Ustaw wartości współczynników , , w taki sposób, by otrzymany przez Ciebie wykres odpowiadał opisanym w tabeli funkcjom kwadratowym. Następnie odczytaj współrzędne punktów, w których podane funkcje mają swoje ekstrema i wpisz w tabelę poprawne liczby.
| Wzór funkcji | Położenie ekstremum (współrzędna wierzchołka paraboli) | Wartość ekstremum (współrzędna wierzchołka paraboli) |
|---|---|---|
Dla podanych funkcji kwadratowych określ, czy posiadają one minimum czy maksimum globalne. Przeciągnij poprawne wartości w odpowiednie miejsca.
, , , , maksimum globalne, minimum globalne, maksimum globalne, minimum globalne
| Funkcja | Ekstremum globalne |
|---|---|