Przeczytaj
Jeśli dwa kwadraty są podobnepodobne w skali , to stosunek ich pól jest równy . Korzystając z tego faktu stwierdzamy na przykład, że .
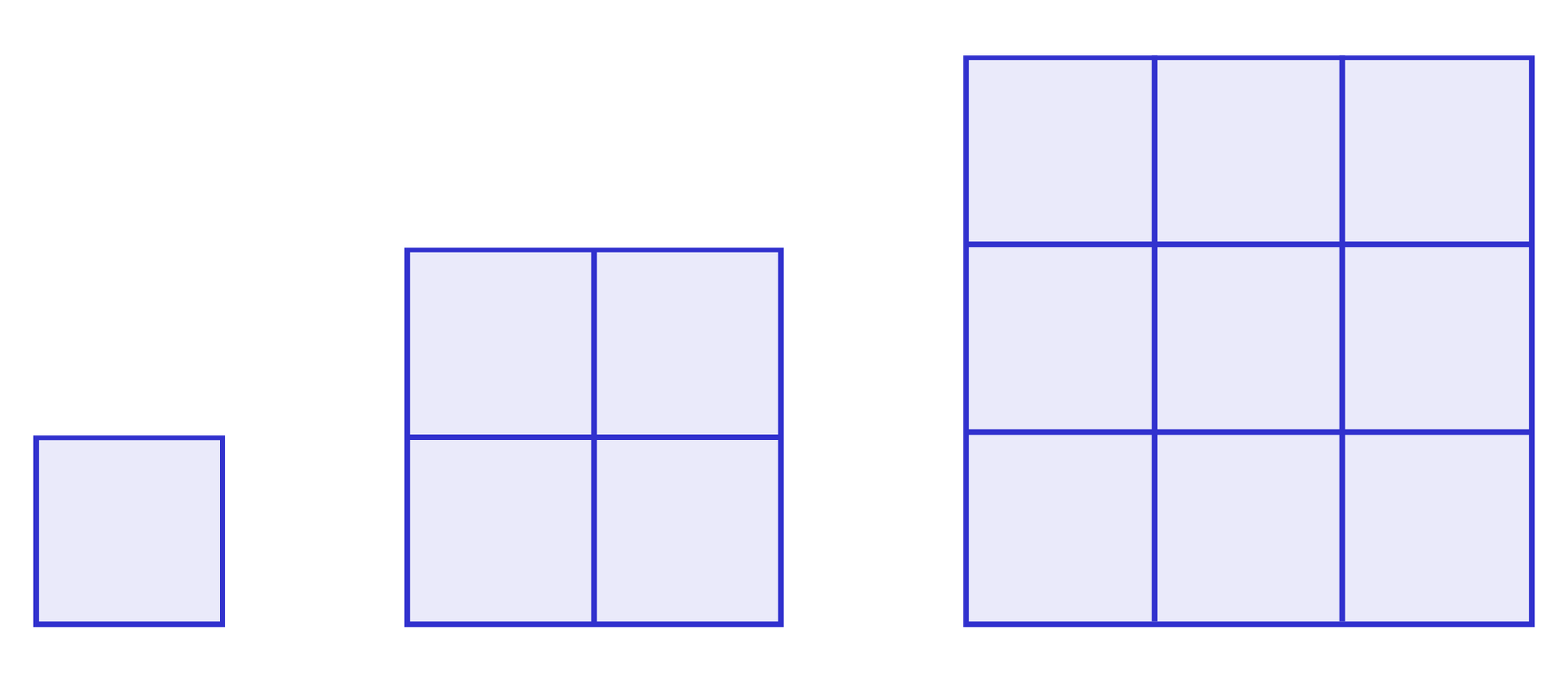
Zauważmy, że jeżeli bok jednego z tych kwadratów oznaczymy przez , to bok drugiego jest równy , co oznacza, że stosunek pól tych kwadratów jest równy
.
Przekonamy się, że tak samo rzecz ma się z trójkątami.
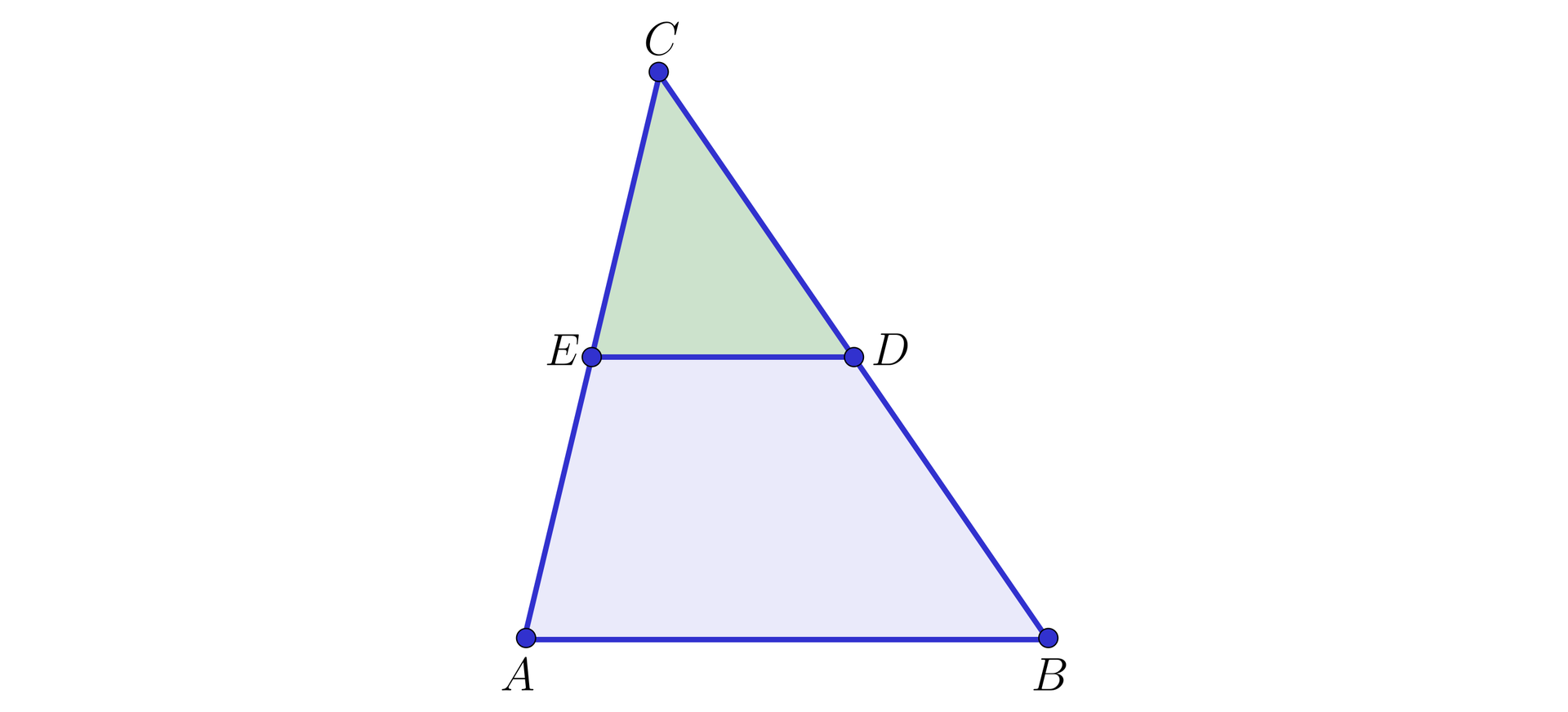
Załóżmy, że trójkąt jest podobny do trójkąta w skali .
Niech odcinek będzie wysokością opuszczoną na bok , a odcinek – wysokością opuszczoną na bok (zobacz rysunek poniżej).

Pole trójkąta jest zatem równe , a pole trójkąta jest równe .
Zauważmy, że z podobieństwa trójkątów oraz wynika, że .
Ponadto trójkąty i są podobne (na podstawie cechycechy ), a ponieważ , więc mamy także .
Stąd:
.
Oznacza to, że stosunek pól rozpatrywanych trójkątów podobnych jest równy .
Udowodniliśmy w ten sposób twierdzenie:
Stosunek pól trójkątów podobnych jest równy kwadratowi skali ich podobieństwa.
W trójkącie połączono odcinkiem środki boków oraz . Trójkąty oraz są podobne w skali . A zatem pole trójkąta jest razy większe od pola trójkąta .
W trójkącie prostokątnym , o przyprostokątnych oraz i przeciwprostokątnej , poprowadzono z wierzchołka kąta prostego wysokość , która podzieliła dany trójkąt na dwie części. Wyznaczmy pola każdego z trójkątów otrzymanych w ten sposób.
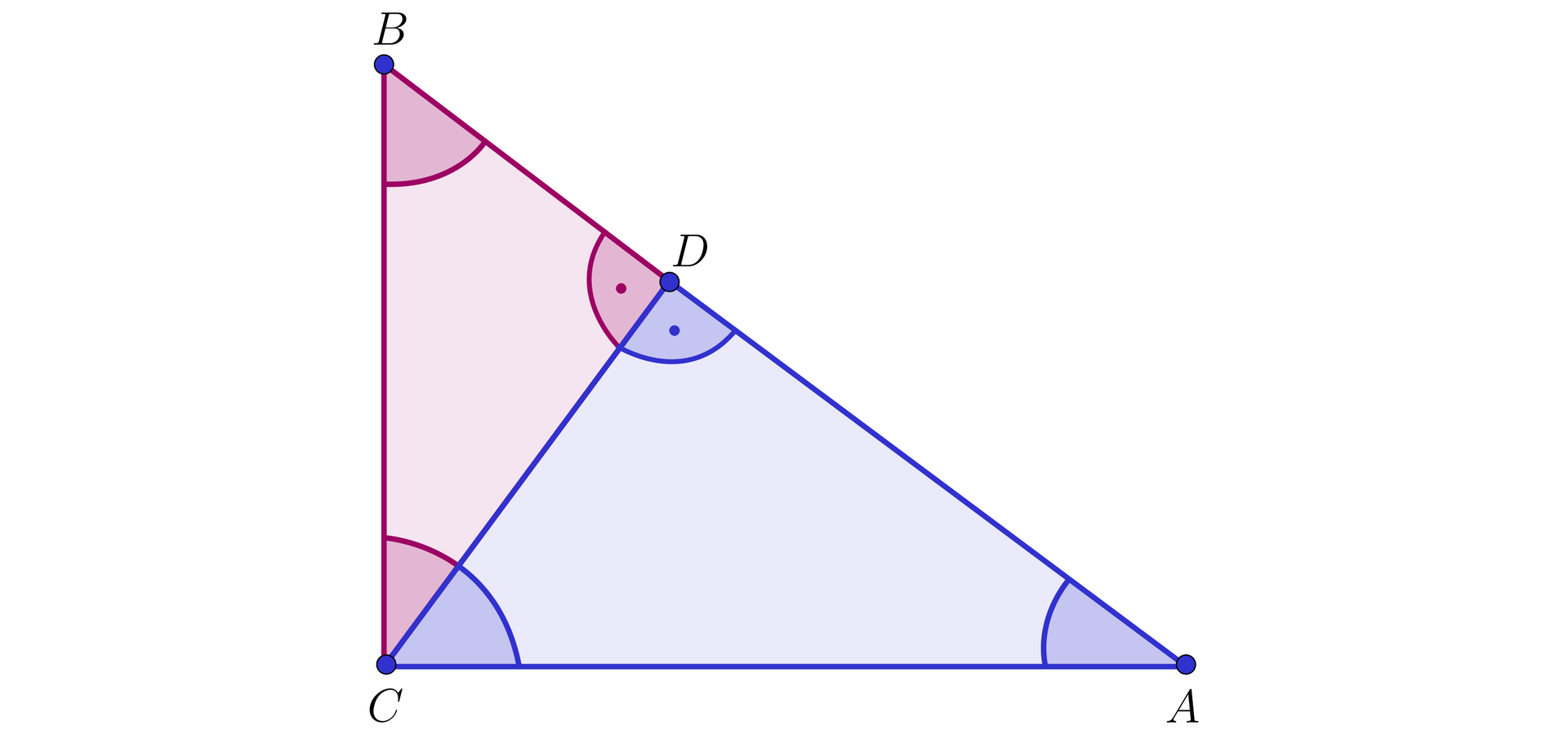
Rozwiązanie. Obliczamy pole rozpatrywanego trójkąta:
.
Trójkąt jest podobny (na podstawie cechy ) do trójkąta w skali , zatem jego pole jest równe
.
Trójkąt jest podobny (na podstawie cechy ) do trójkąta w skali , a więc jego pole jest równe
.
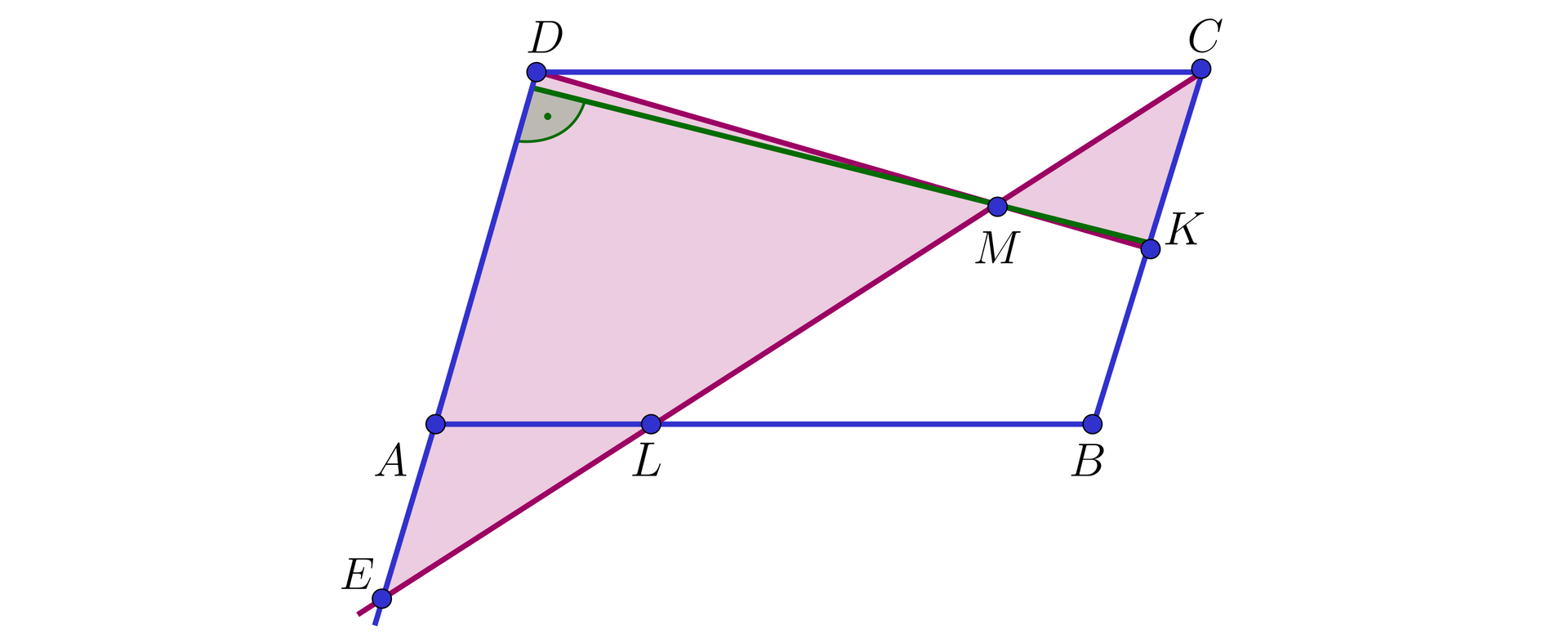
Na boku trójkąta leży punkt . Prosta przechodzi przez , jest równoległa do i przecina bok w punkcie . Prosta przechodzi przez , jest równoległa do i przecina bok w punkcie (zobacz rysunek).
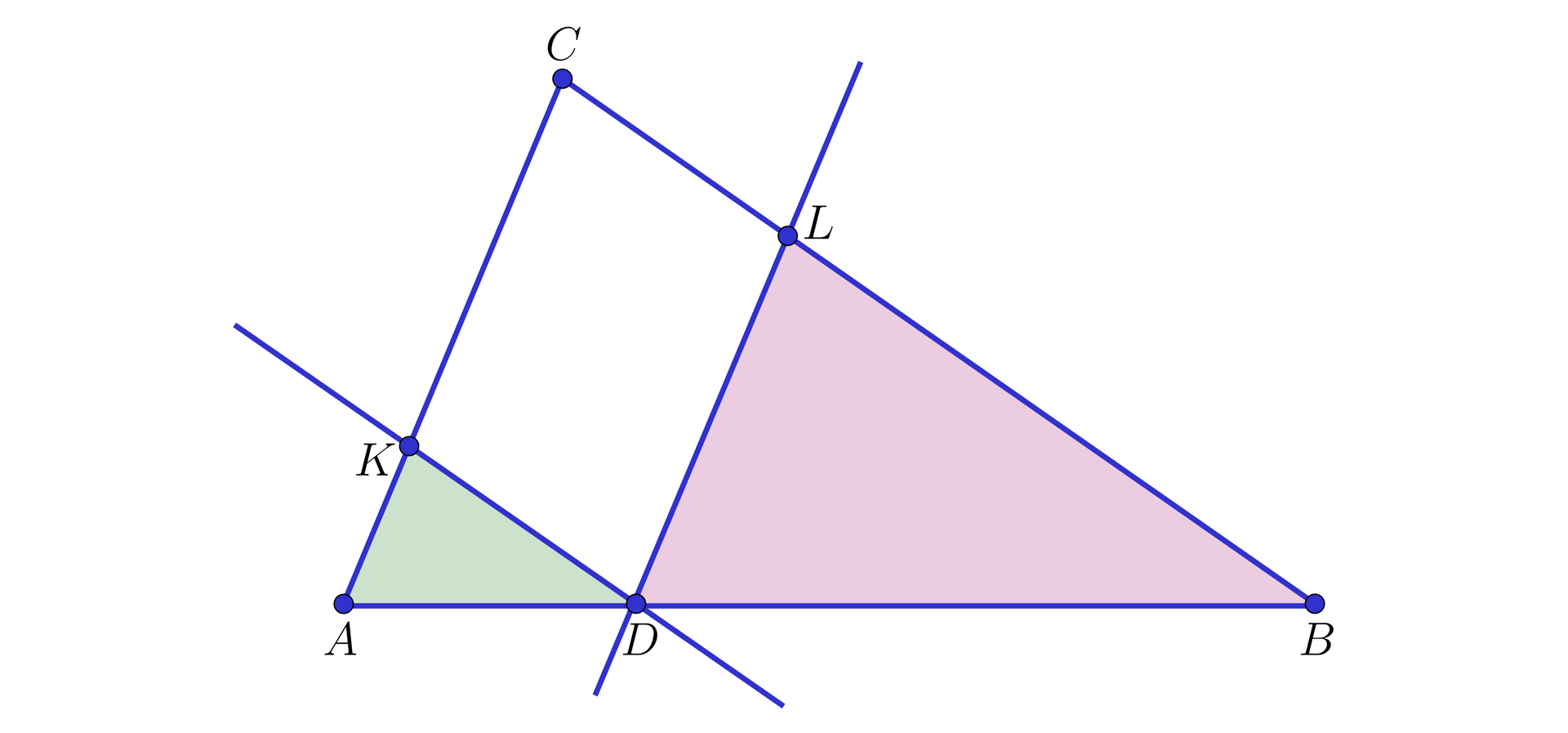
Pole trójkąta jest równe , a pole trójkąta jest równe .
Obliczymy pole trójkąta .
Rozwiązanie.
Oznaczmy pole trójkąta przez .
Zauważmy, że:
ponieważ , więc trójkąty i są podobne na mocy cechy , w skali ; oznacza to, że , skąd , , czyli ,
ponieważ , więc trójkąty i są podobne na mocy cechy , w skali ; oznacza to, że , skąd , , czyli
Uwzględniając powyższe spostrzeżenia w równości otrzymujemy zależność
,
skąd
czyli .
Zatem pole trójkąta jest równe .
Uwaga . Założmy, jak w powyższym przykładzie, że na boku trójkąta leży punkt , a na bokach i takie punkty, odpowiednio, i , że oraz .
Pokażemy, że jeśli i , to
.
Rozumując podobnie, jak w rozwiązaniu powyższego przykładu, opisujemy podobieństwo trójkątów , i , a stąd otrzymujemy zależności
oraz ,
a więc oraz .
Stąd ,
,
,
czyli .
Zauważmy przy okazji, że ponieważ oraz , więc .
Uwaga . Założmy że wewnątrz trójkata leży punkt , a na bokach , i leżą takie pary punktów, odpowiednio, i , i oraz i , że , oraz , przy czym proste , i przecinają się w punkcie (zobacz rysunek).

Pokażemy, że jeśli , i , to
.
Zauważmy mianowicie, że na podstawie Uwagi możemy zapisać następujące zależności:
, przy czym ,
, przy czym ,
.
Oznacza to, że
.
Koniec dowodu.
W czworokącie punkty , , , są środkami boków, odpowiednio, , , oraz , a proste i przecinają się w punkcie (jak na poniższym rysunku).
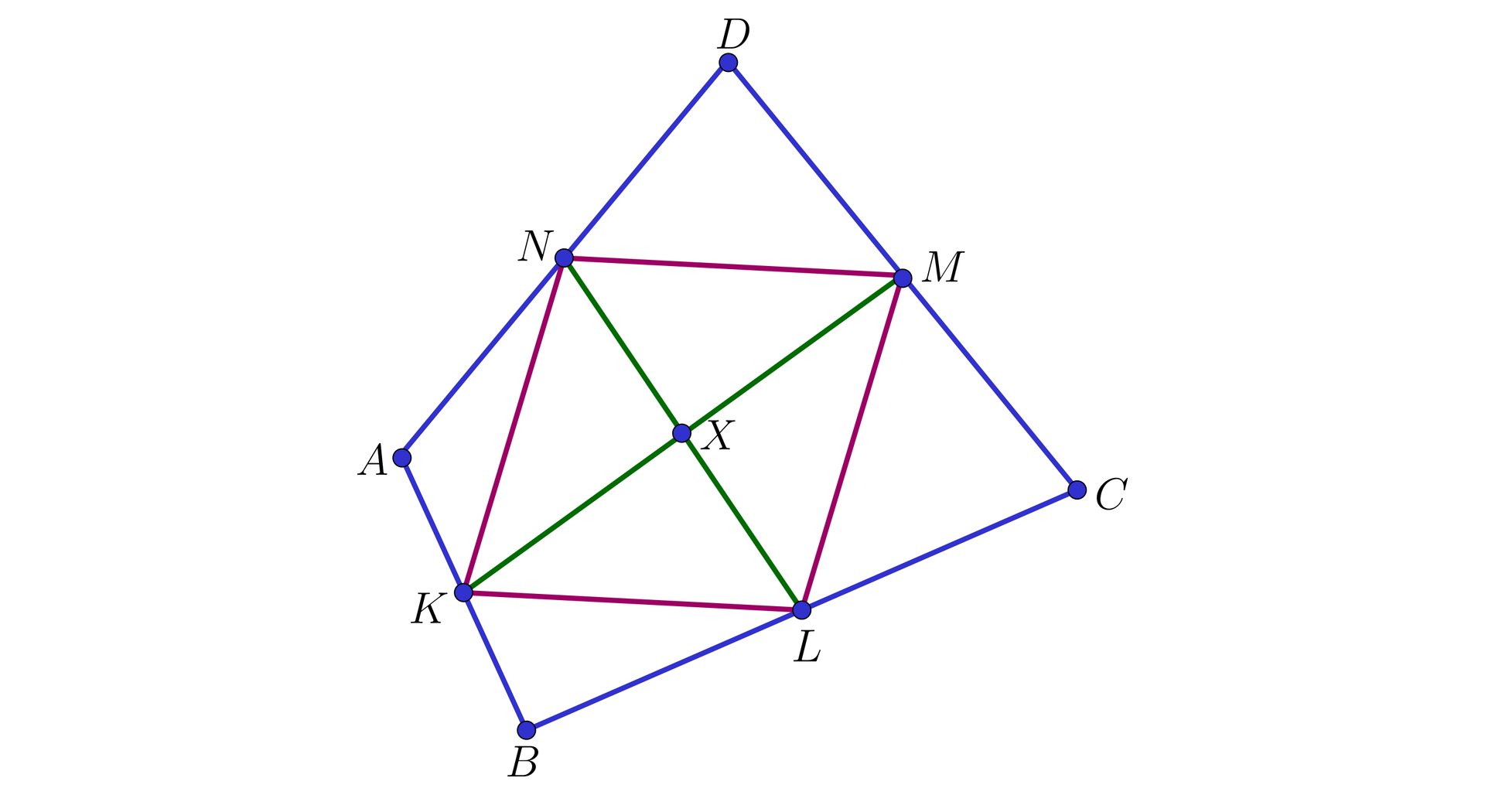
Wykażemy, że:
a) suma pól trójkątów i jest równa sumie pól trójkątów i .

b) suma pól czworokątów i jest równa sumie pól czworokątów i .
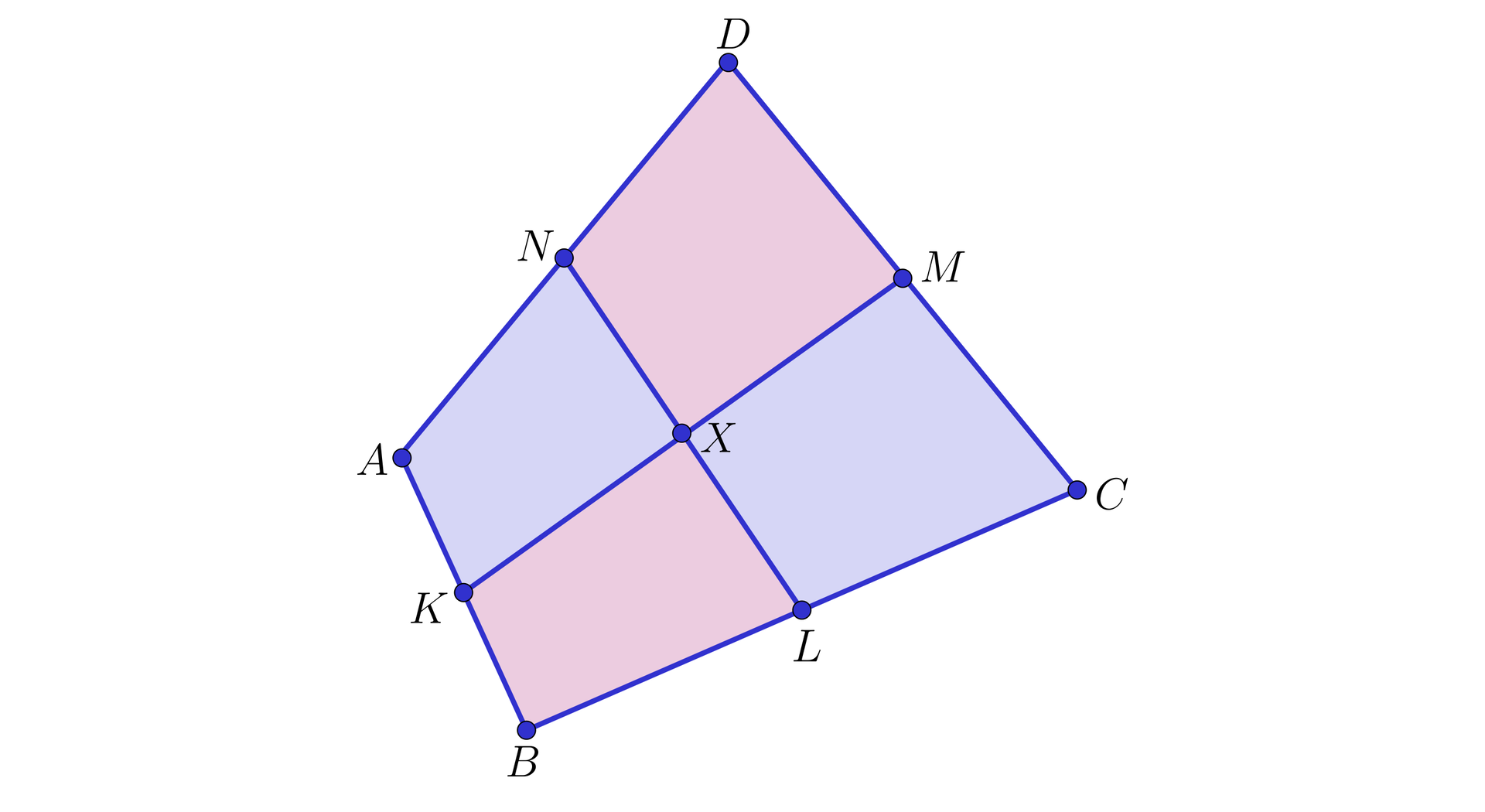
Rozwiązanie.
Prowadzimy przekątną i korzystamy z twierdzenia o linii środkowej.

Otrzymujemy, że:
w trójkącie : i , co oznacza, że trójkąty oraz są podobne (na podstawie cechy ), w skali .
Wynika stąd, że , czyli ,w trójkącie : i , co oznacza, że trójkąty oraz są podobne (na podstawie cechy ), w skali .
Wynika stąd, że , czyli .
Wobec tego .
Prowadzimy teraz przekątną i ponownie korzystamy z twierdzenia w linii środkowej w trójkątach i .
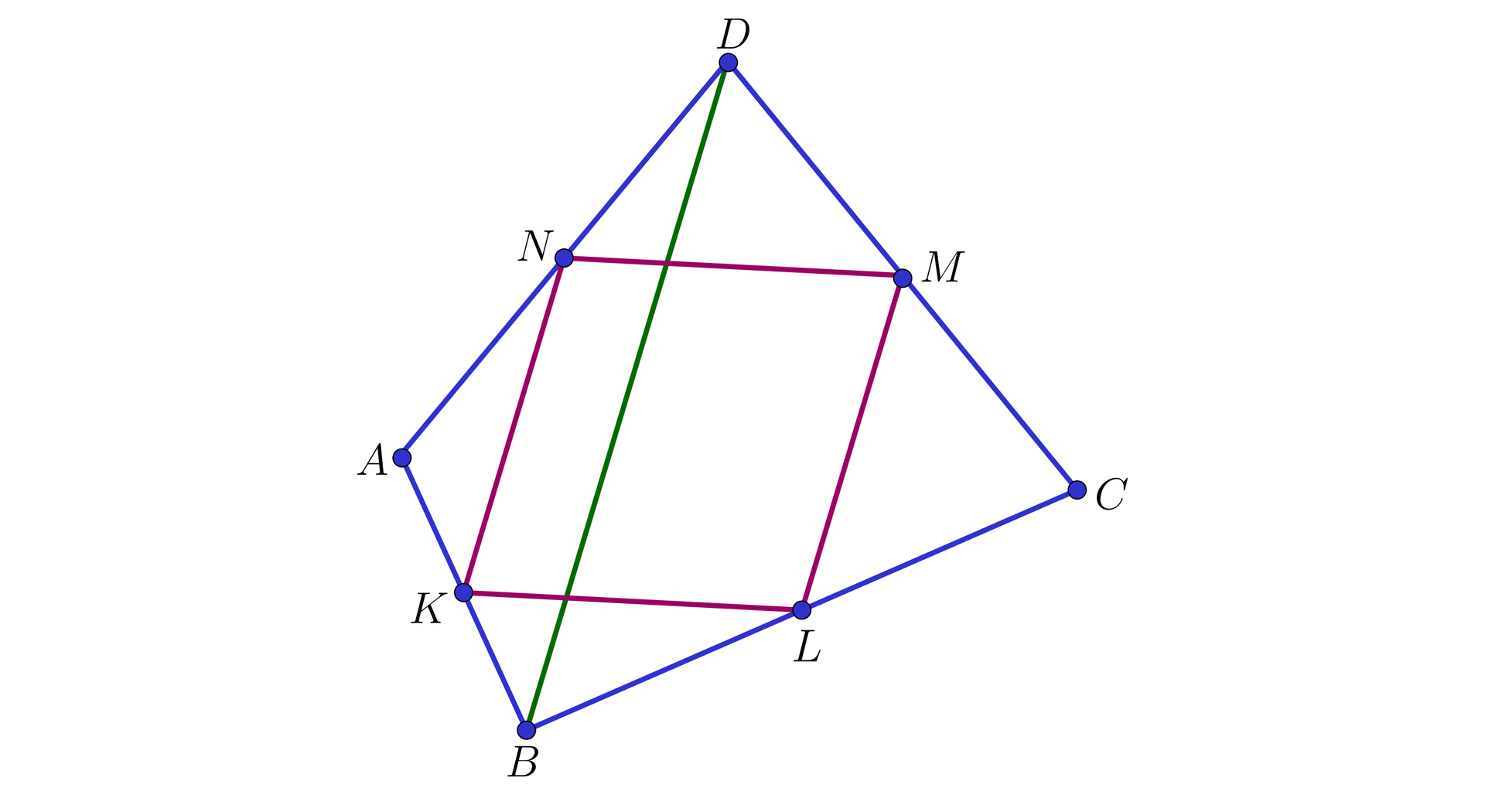
Rozumując podobnie, jak w poprzednim przypadku otrzymujemy, że oraz , skąd .
Wobec tego , a to właśnie mieliśmy udowodnić.
b) Na podstawie spostrzeżeń poczynionych powyżej stwierdzamy, że:
,pary przeciwległych boków czworokąta są równe, a więc jest on równoległobokiem, czyli jego przekątne przecinają się w połowie.
Oznacza to, że
.
Wynika stąd, że
,
skąd otrzymujemy, że
,
a więc suma pól czworokątów i jest równa sumie pól czworokątów i .
W ten sposób dowód został zakończony.
Uwaga.
Korzystając z wniosków zapisanych w powyższym przykładzie udowodnimy następującą własność.
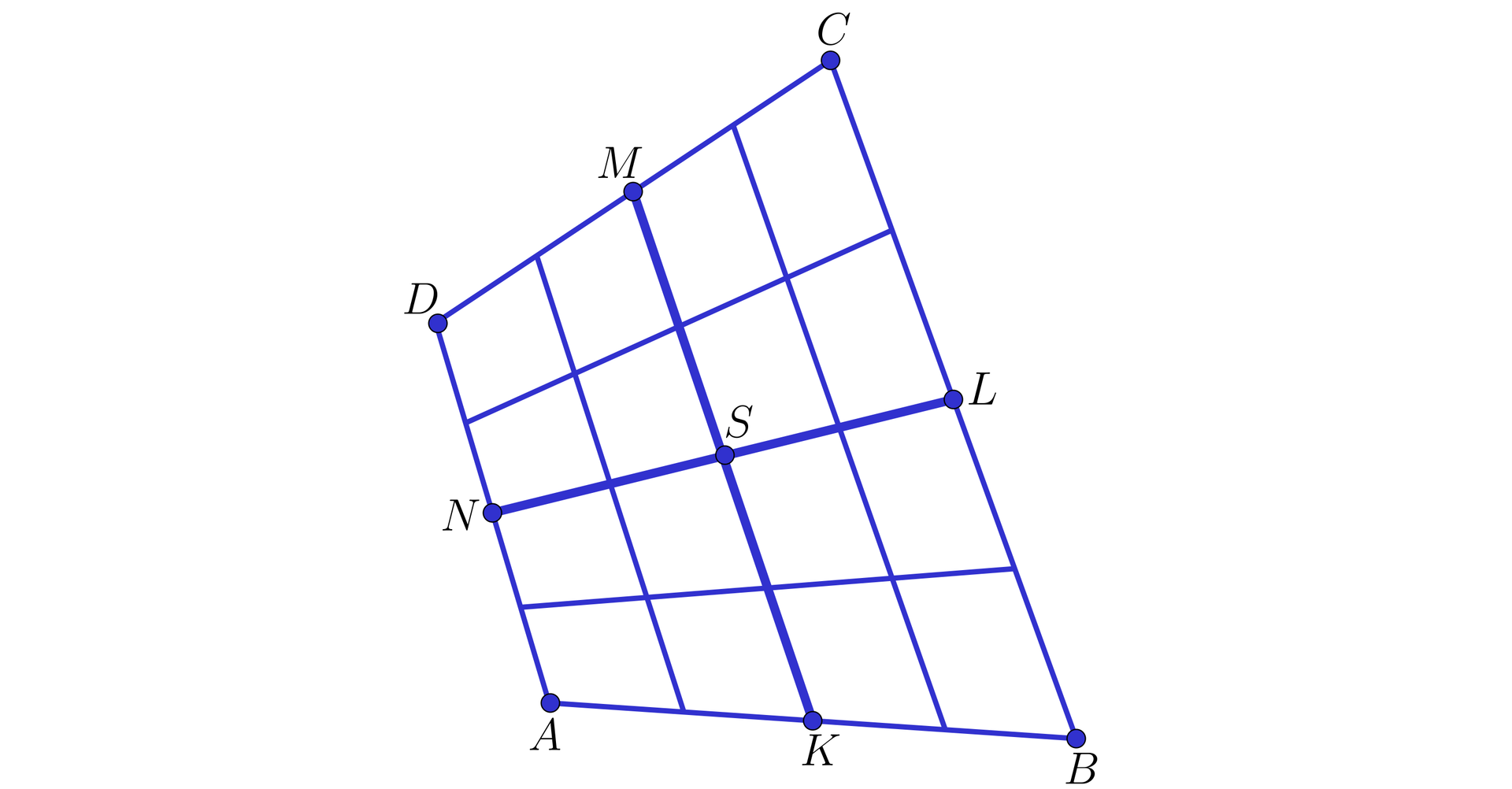
Jeżeli każdy bok czworokąta wypukłego podzielimy na cztery równe części, a następnie:
punkty podziału połączymy tak, żeby otrzymać podział na czworokątów,
pomalujemy czworokąty otrzymane w wyniku tego podziału na dwa kolory tak, żeby otrzymać szachownicę (jak na rysunku poniżej),
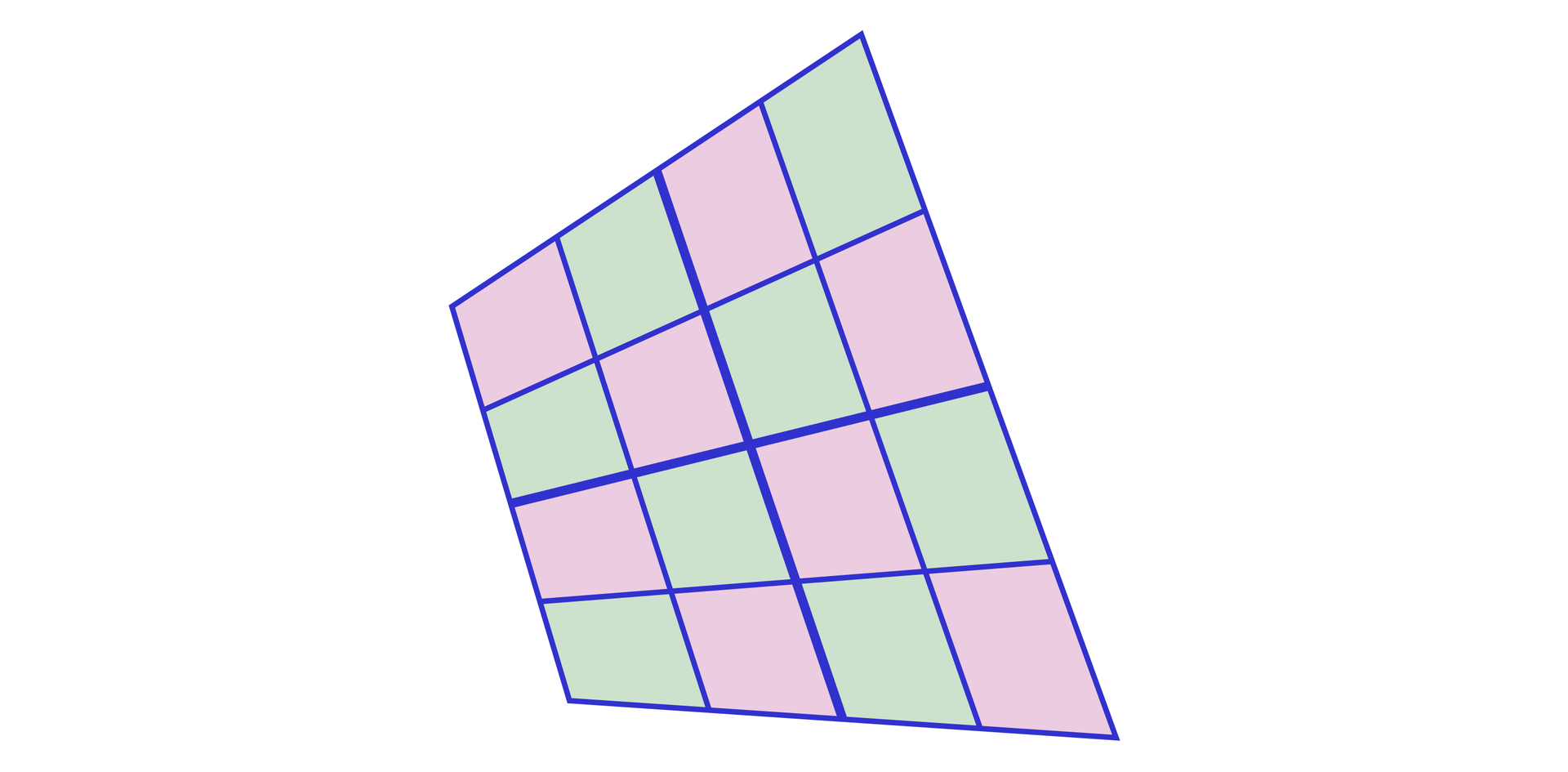
to sumy pól wielokątów w każdym z tych dwóch kolorów są równe.
Dla dowodu przyjmijmy, że rozpatrujemy własności czworokąta , którego środkami boków są punkty , , oraz , a jest punktem przecięcia odcinków i (jak na poniższym rysunku).
Wobec tego czworokąt jest równoległobokiem, a więc punkt jest środkiem każdej z jego przekątnych i , a także prawdziwa jest równość
.
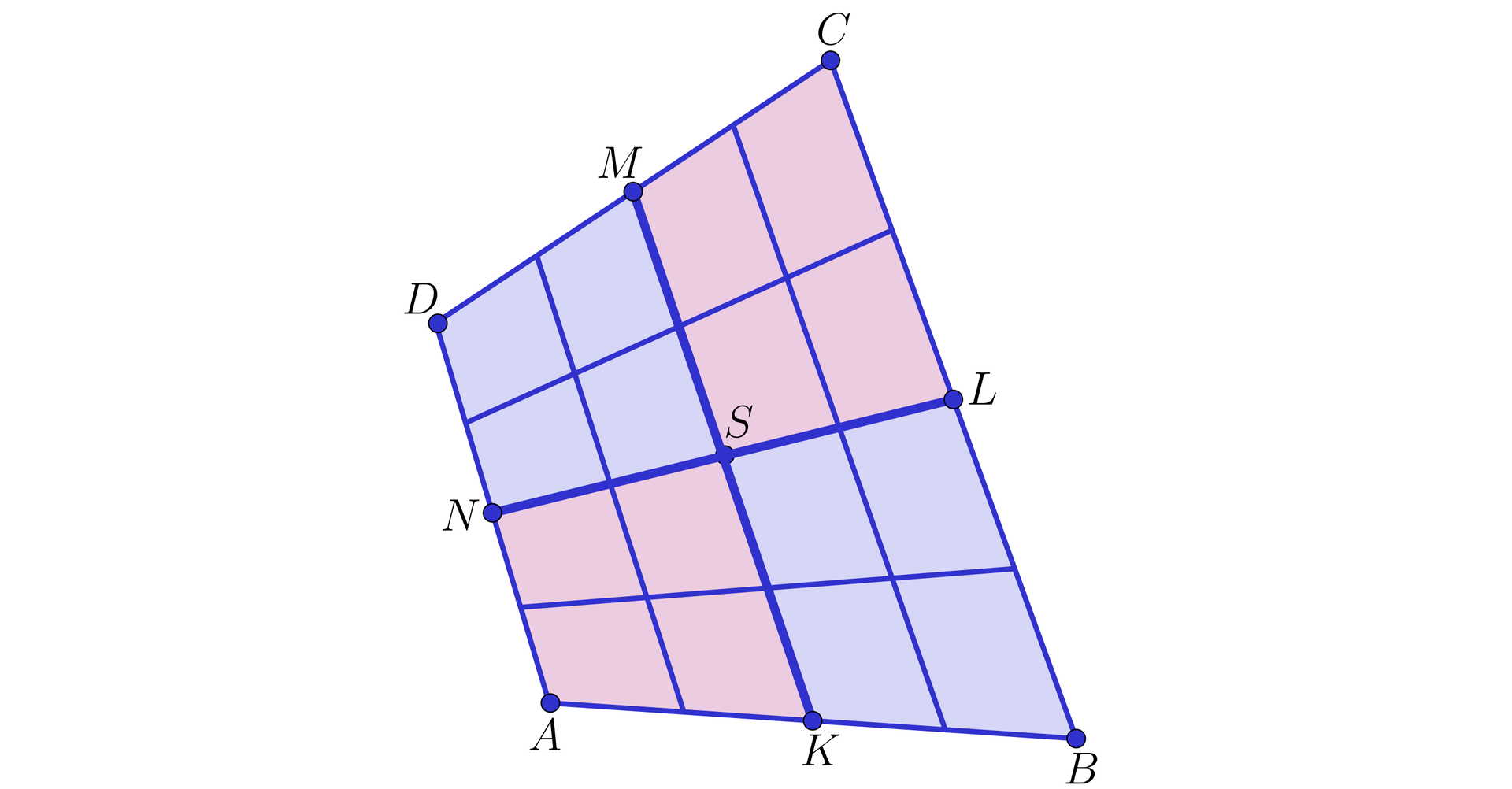
Oznaczmy z kolei: środek odcinka przez , środek odcinka przez , a przez – punkt przecięcia odcinków i .

Ponieważ czworokąt ma wierzchołki w środkach boków czworokąta , więc jest równoległobokiem, zatem punkt jest środkiem każdej z jego przekątnych, w szczególności jest to środek odcinka .
Oznaczmy następnie: środek odcinka przez , środek odcinka przez , a przez – punkt przecięcia odcinków i .

Ponieważ czworokąt ma wierzchołki w środkach boków czworokąta , więc jest równoległobokiem, zatem punkt jest środkiem każdej z jego przekątnych, w szczególności jest to środek odcinka .
Wynika stąd, że czworokąt ma wierzchołki w środkach boków czworokąta .
Oznaczmy przez punkt przecięcia przekątnych równoległoboku .

Wówczas prawdziwa jest równość .
Rozumując podobnie, wykazujemy równości par pól odpowiednich wielokątów otrzymanych z podziału czworokątów : , oraz , skąd dostajemy tezę.
W równoległoboku punkt jest środkiem boku , a na boku leży taki punkt , że . Proste i przecinają się w punkcie (jak na poniższym rysunku).
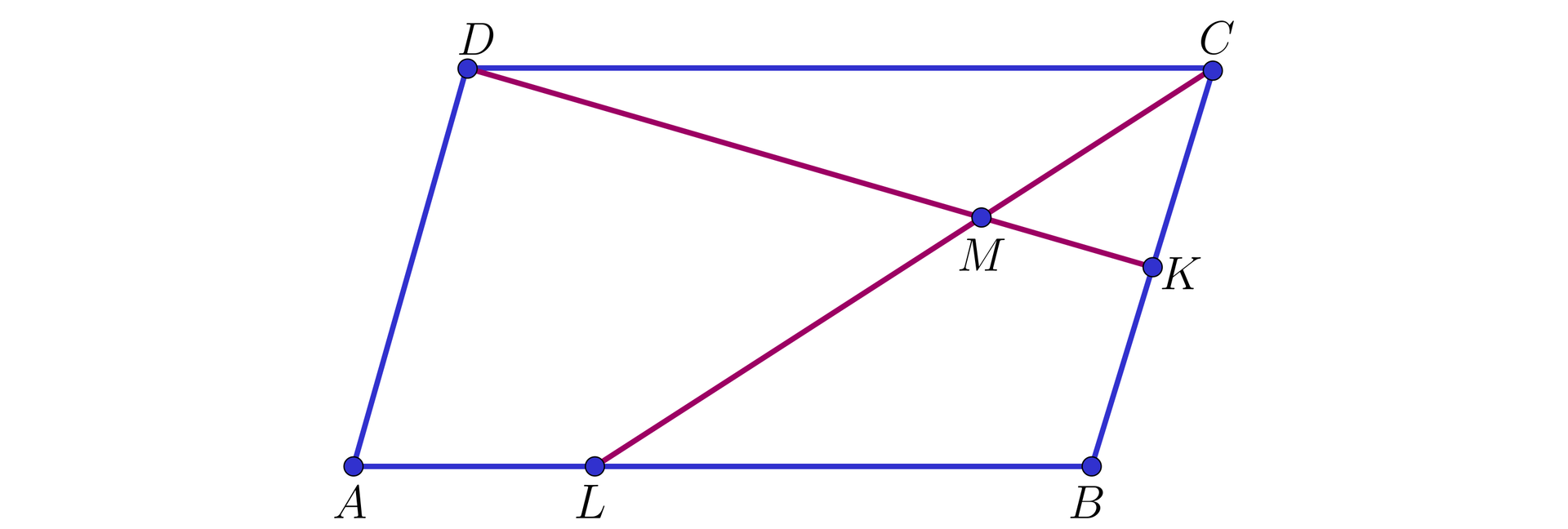
Obliczymy pole czworokąta , wiedząc, że pole równoległoboku jest równe .
Rozwiązanie.
Przyjmujemy oznaczenia: oraz .
Zatem z warunków zadania otrzymujemy, że:
, ,
, .
Oznaczmy ponadto:
długość wysokości równoległoboku poprowadzonej z wierzchołka na bok przez (wobec tego jest odległością między prostymi równoległymi i ),
długość wysokości równoległoboku poprowadzonej z wierzchołka na bok przez (wobec tego jest odległością między prostymi równoległymi i ).
Używając powyższych oznaczeń możemy zapisać:
pole równoległoboku jako lub ,
pole trójkąta jako ,
pole trójkąta jako .
Dalszą część rozwiązania przedstawimy na kilka sposobów.
sposób
Środek odcinka oznaczamy przez .
Wtedy odcinek to linia środkowa w trójkącie , co oznacza, że i .

Wobec tego trójkąty i są podobne (na mocy cechy ), w skali . Zatem , skąd , a także .
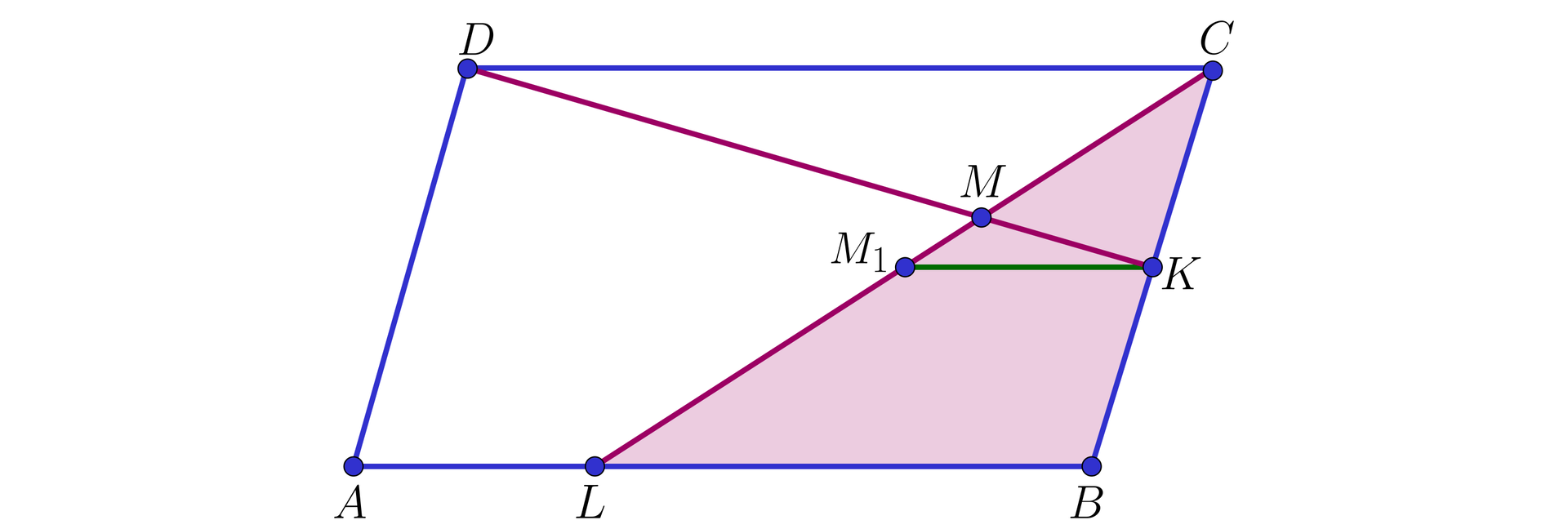
Ponieważ , więc , skąd wynika, że trójkąty i są podobne (na mocy cechy ), w skali , zatem .
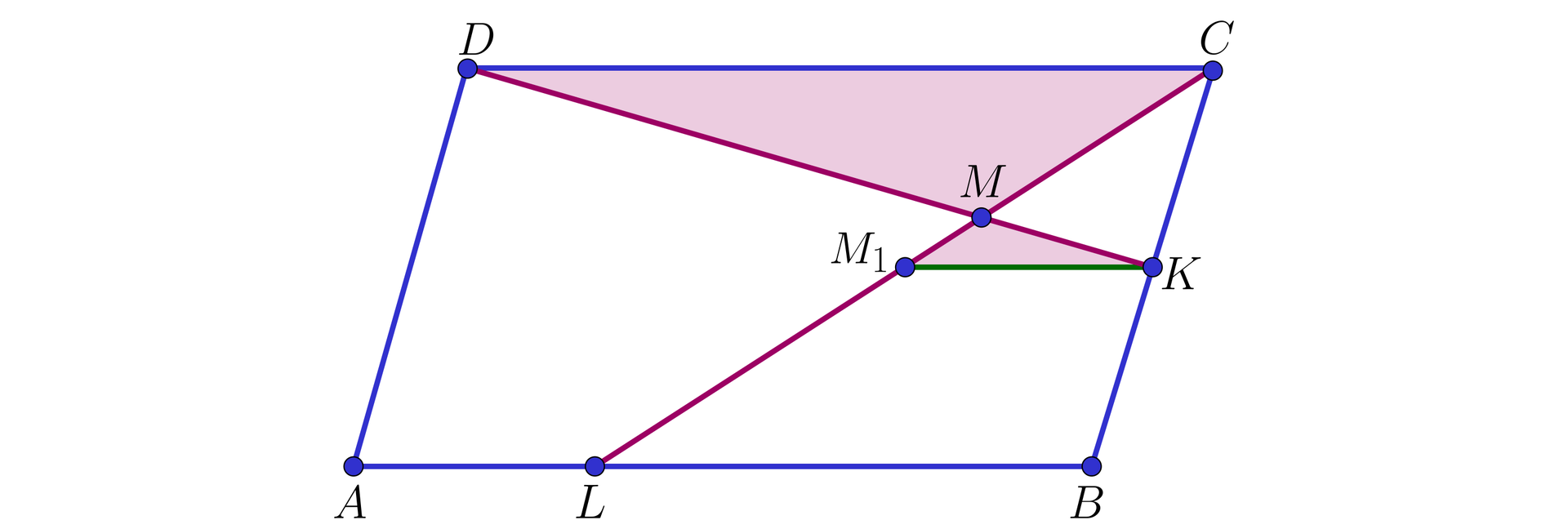
Ponieważ trójkąty i mają wspólny wierzchołek , więc .
Stąd , czyli
.
sposób
Oznaczmy przez punkt przecięcia prostych i .

Ponieważ i , więc na podstawie cechy kbk trójkąty oraz są przystające.
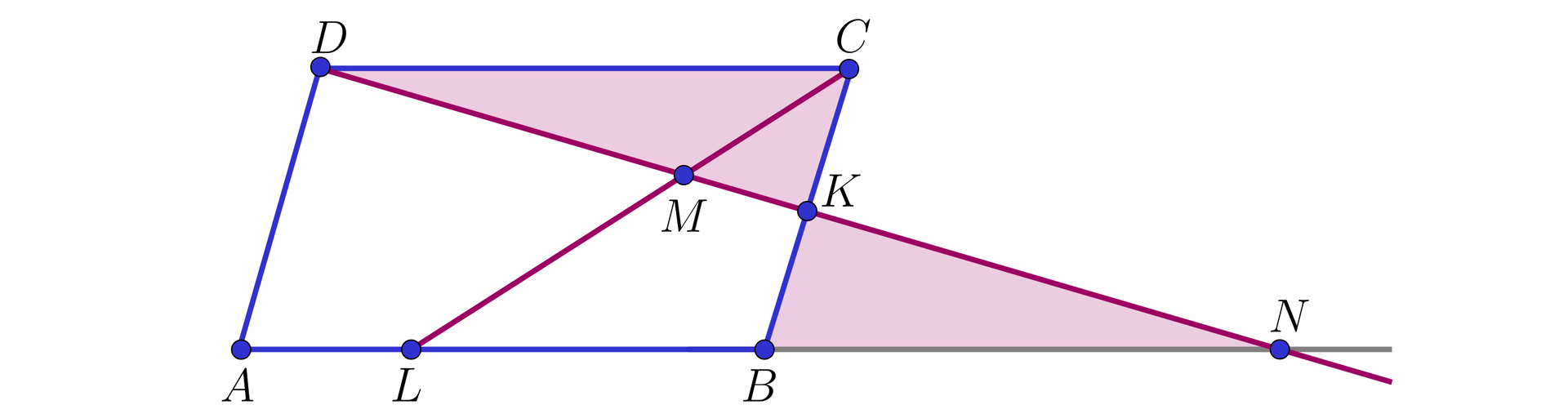
Wynika stąd, że:
,
, a więc .
Ponieważ , więc na podstawie cechy trójkąty oraz są podobne, przy czym skala tego podobieństwa jest równa , skąd .
Ponadto w tej właśnie skali pozostają wysokości poprowadzone z wierzchołka w trójkątach oraz , co oznacza, że w pierwszym z nich ta wysokość jest równa , a w drugim jest równa .

Wobec tego
.
Ostatecznie stwierdzamy, że
.
sposób
Oznaczmy przez punkt przecięcia prostych i .
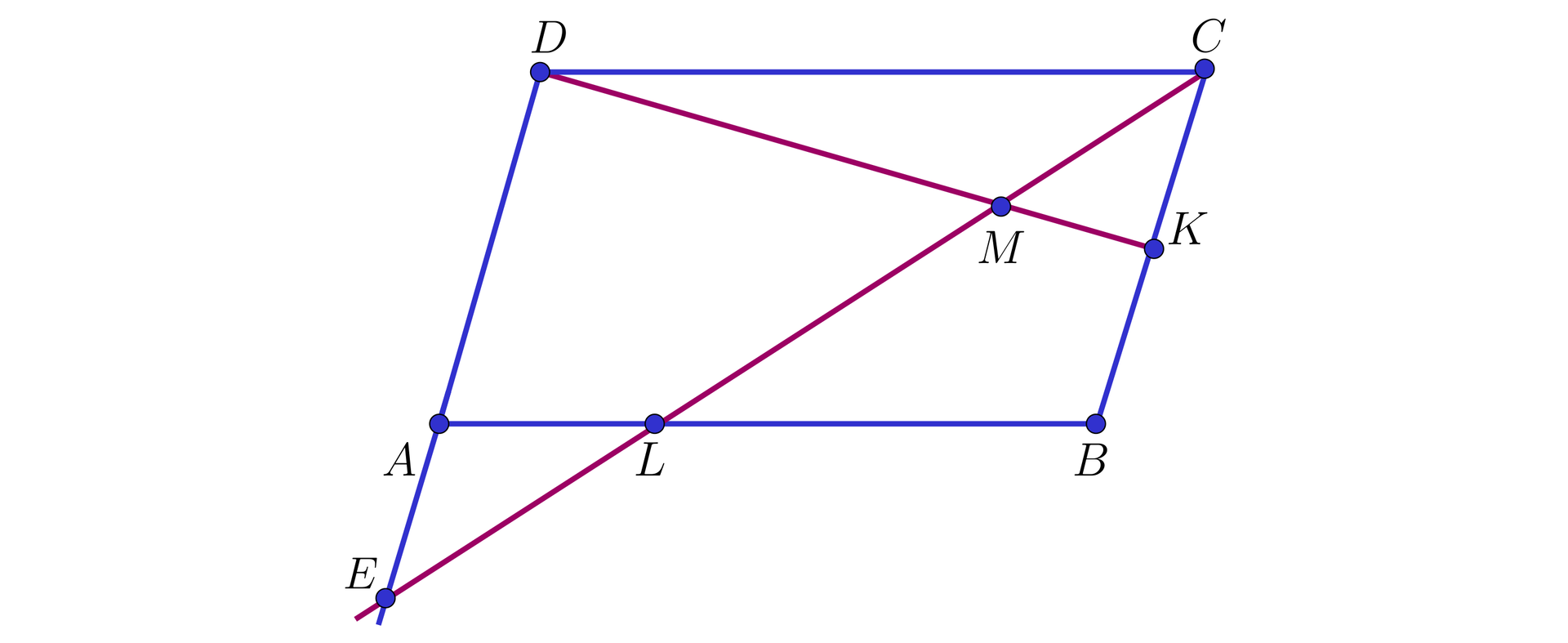
Ponieważ i , więc na podstawie cechy trójkąty oraz są podobne, w skali .
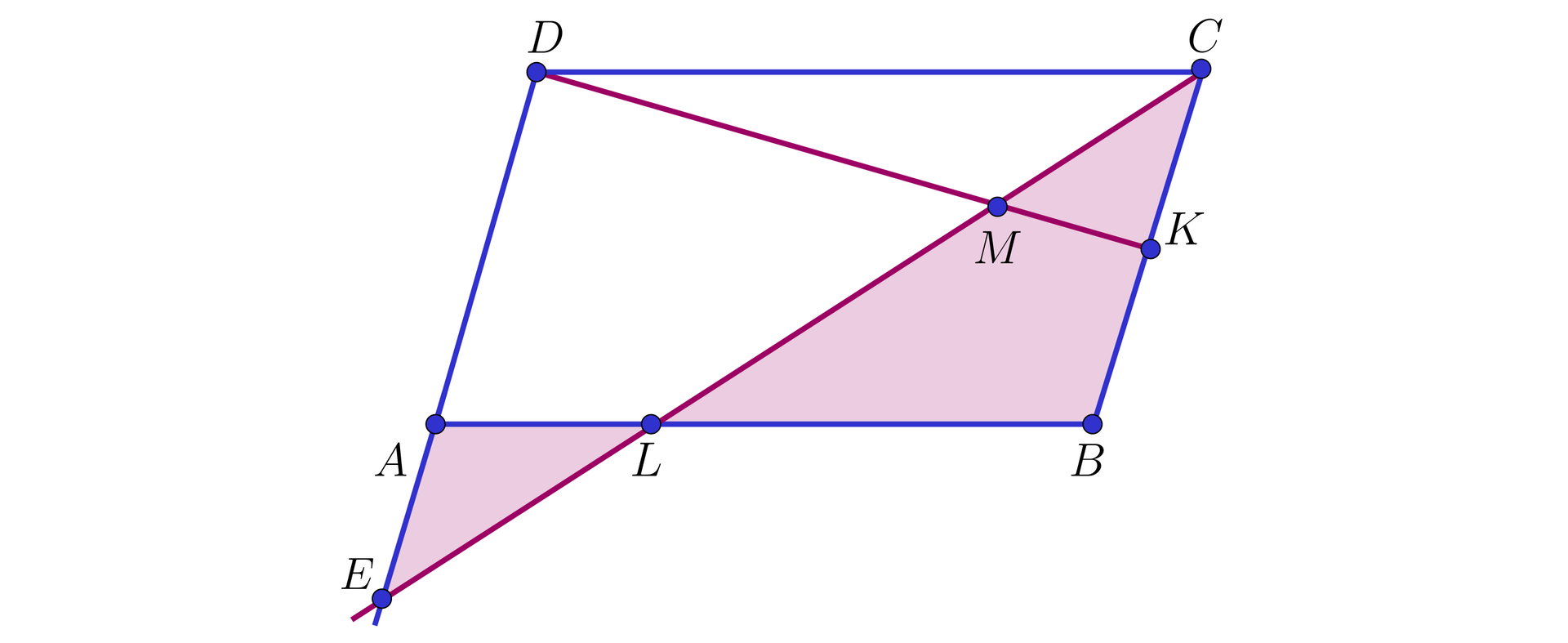
Wobec tego:
, czyli ,
, skąd , czyli .
Ponieważ , więc na podstawie cechy trójkąty i są podobne, przy czym skala tego podobieństwa jest równa , skąd .
Oznacza to, że stosunek długości wysokości poprowadzonych z wierzchołka w trójkątach i jest także równy , skąd wynika, że w pierwszym z tych trójkątów taka wysokość jest równa , a w drugim z niech jest równa .
Zatem , skąd , czyli .
Słownik
figury, z których jedna jest obrazem drugiej w pewnym podobieństwie
warunki konieczne i wystarczające na to, aby dwa trójkąty były podobne