Przeczytaj

Przypomnijmy definicje funkcji trygonometrycznych kąta ostregofunkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym.

Narysujmy trójkąt prostokątny o przyprostokątnych długości $a$ i $b$ , przeciwprostokątnej $c$ oraz kątach ostrych $α$ i $β$ .

R3d1s3GaB5fLz

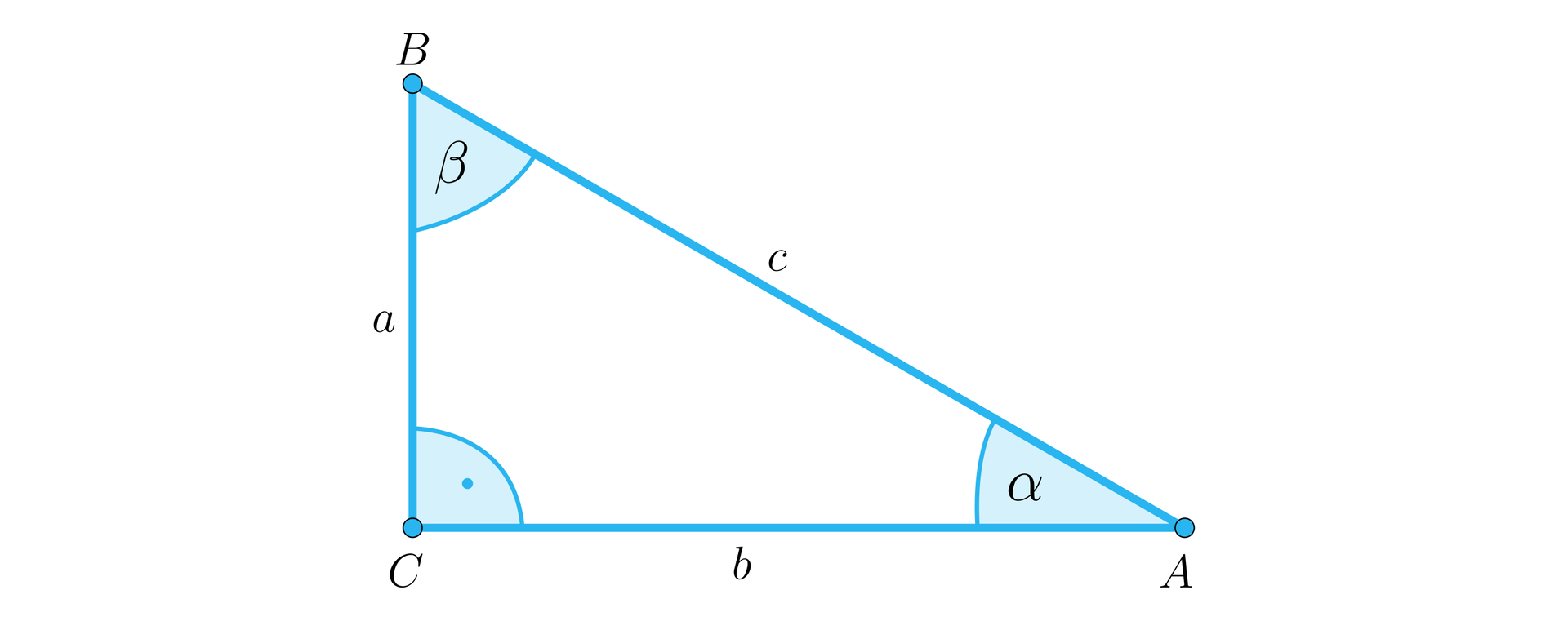
Rysunek przedstawia trójkąt prostokątny o podstawie b, która jest jednocześnie bokiem CA, o pionowej przyprostokątnej a, która jest bokiem BC oraz o przeciwprostokątnej c, która jest bokiem BA. Na ilustracji zaznaczono kąty wewnętrze trójkąta. Przy wierzchołku C znajduje się kąt prosty, przy wierzchołku B znajduje się kąt β, a przy wierzchołku A znajduje się kąt α.

Wówczas:

Sinusem kąta ostrego nazywamy stosunek długości przyprostokątnej leżącej naprzeciwko tego kąta do długości przeciwprostokątnej, czyli

$\sin α = \frac{a}{c}$ oraz $\sin β = \frac{b}{c}$ .

Cosinusem kąta ostrego nazywamy stosunek długości przyprostokątnej leżącej przy tym kącie do długości przeciwprostokątnej, czyli

$\cos α = \frac{b}{c}$ oraz $\cos β = \frac{a}{c}$ .

Tangensem kąta ostrego nazywamy stosunek długości przyprostokątnej leżącej naprzeciwko tego kąta do długości przyprostokątnej leżącej przy tym kącie, czyli

$tg α = \frac{a}{b}$ oraz $tg β = \frac{b}{a}$ .

Dla kąta $α \in (0, 90 °)$ zachodzą następujące zależności:

$\sin (90 ° - α) = \cos α$ ,

$\cos (90 ° - α) = \sin α$ ,

$tg (90 ° - α) = \frac{1}{tg α}$ .

Powyższe zależności nazywamy wzorami redukcyjnymi. Do odczytywania przybliżonych wartości funkcji trygonometrycznych posłużymy się tablicami wartości funkcji trygonometrycznych.

Przykład 1

Sprawdzimy, czy wartość wyrażenia $\frac{\sin 32 ° - \cos 44 °}{tg 12 ° - \sin 83 °}$ jest ujemna.

Rozwiązanie:

Jeżeli wykorzystamy tablice wartości funkcji trygonometrycznych, to wartość wyrażenia jest równa:

$\frac{\sin 32 ° - \cos 44 °}{tg 12 ° - \sin 83 °} = \frac{0, 5299 - 0, 7193}{0, 2126 - 0, 9925} = \frac{- 0, 1894}{- 0, 7799} = 0, 243 > 0$ .

Zatem wartość podanego wyrażenia nie jest ujemna.

Przykład 2

Wiedząc o tym, że $\sin α = 0, 682$ , obliczymy wartość wyrażenia $\frac{2 \cdot \sin α - 3 \cdot \cos (90 ° - α)}{3 \cdot \sin α + 2 \cdot \cos (90 ° - α)} + \sin α$ .

Rozwiązanie:

Zauważmy, że

$\frac{2 \cdot \sin α - 3 \cdot \cos (90 ° - α)}{3 \cdot \sin α + 2 \cdot \cos (90 ° - α)} + \sin α = \frac{2 \cdot \sin α - 3 \cdot \sin α}{3 \cdot \sin α + 2 \cdot \sin α} + \sin α =$

$= \frac{- \sin α}{5 \cdot \sin α} + \sin α = - \frac{1}{5} + \sin α = - 0, 2 + 0, 682 = 0, 482$ .

W kolejnym przykładzie skorzystamy z faktu, że tangens kąta nachylenia prostej do osi odciętych w układzie współrzędnych jest równy współczynnikowi kierunkowemu $a$ ze wzoru $y = a x + b$ .

Przykład 3

Podamy przybliżone miary kątów ostrych nachylenia prostych do osi $X$ , gdy proste są określone równaniami:

a) $y = \frac{3}{10} x - 2$ ,

b) $y = 3 x + 1$ ,

c) $y = \frac{5}{7} x - 9$ .

Rozwiązanie:

a) Ponieważ $a = \frac{3}{10}$ , zatem $tg α = \frac{3}{10}$ , czyli $α \approx 17 °$

b) Ponieważ $a = 3$ , zatem $tg α = 3$ , czyli $α \approx 72 °$ .

c) Ponieważ $a = \frac{5}{7}$ , zatem $tg α = \frac{5}{7}$ , czyli $α \approx 36 °$ .

Przybliżone wartości funkcji trygonometrycznych służą również do rozwiązywania trójkątów prostokątnych, czyli znajdowania długości wszystkich boków i kątów w trójkącie prostokątnym.

Przykład 4

Obliczymy długości pozostałych boków oraz miary kątów trójkąta, którego przyprostokątne mają długości $3$ i $5$ .

Rozwiązanie:

Narysujmy trójkąt prostokątny i wprowadźmy oznaczenia, jak na poniższym rysunku.

R17eoDgRjPZGL

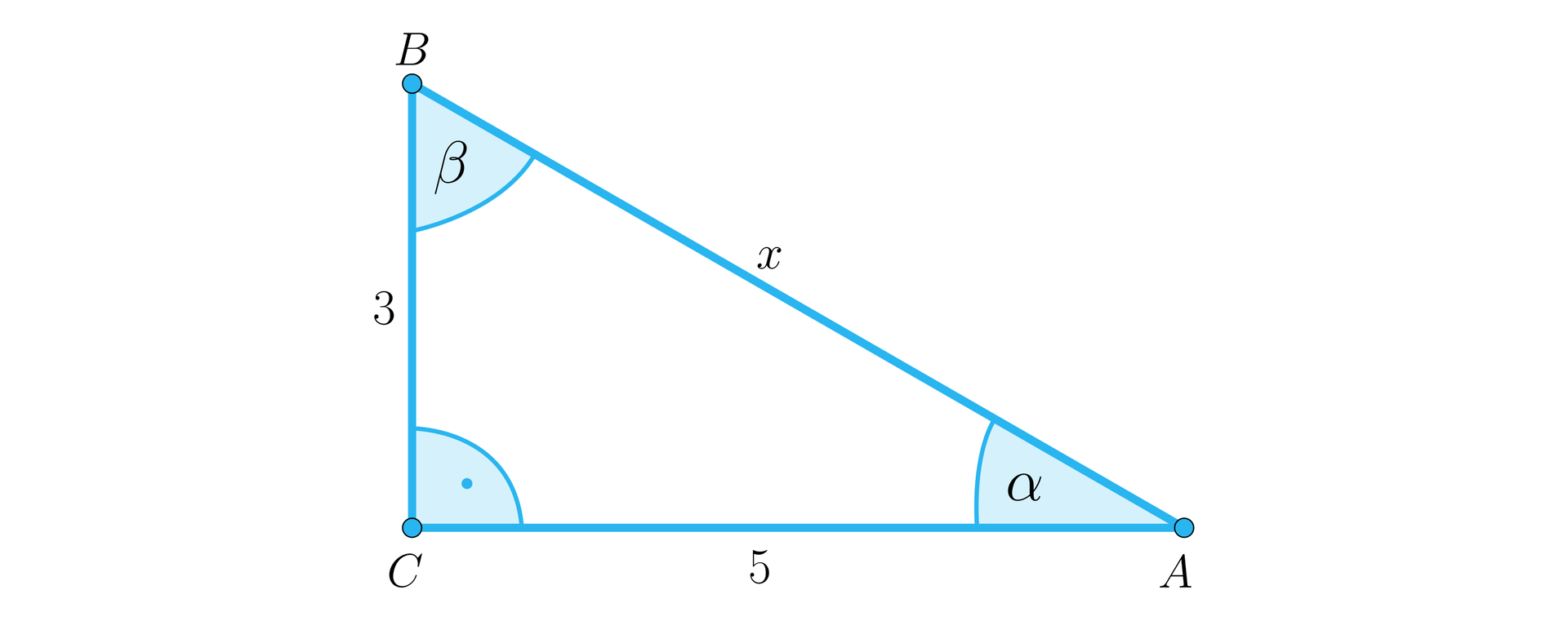
Rysunek przedstawia trójkąt prostokątny o podstawie CA, która ma długość 5, o pionowej przyprostokątnej BC, która ma długość 3 oraz o przeciwprostokątnej BA., która ma nieznaną długość x. Na ilustracji zaznaczono kąty wewnętrze trójkąta. Przy wierzchołku C znajduje się kąt prosty, przy wierzchołku B znajduje się kąt β, a przy wierzchołku A znajduje się kąt α.

Długość przeciwprostokątnej obliczamy z twierdzenia Pitagorasa.

Zatem

$3^{2} + 5^{2} = x^{2}$ .

Wobec tego $x = \sqrt{34}$ .

Do wyznaczenia miar kątów wykorzystamy funkcję trygonometryczną tangens.

Mamy:

$tg β = \frac{5}{3} = 1, 666 . . .$ , czyli $β = 59 °$ ,

$tg α = \frac{3}{5} = 0, 6$ , czyli $α = 31 °$ .

Zauważmy, że mogliśmy wykorzystać definicję funkcji sinus lub cosinus, ponieważ wyznaczyliśmy długość przeciwprostokątnej w tym trójkącie.

Przykład 5

Wyznaczymy przybliżoną wartość kąta zawartego pomiędzy przekątną sześcianu a przekątną jego ściany bocznej.

Rozwiązanie:

Narysujmy sześcian i wprowadźmy oznaczenia, jak na poniższym rysunku.

RjzQszary3szl

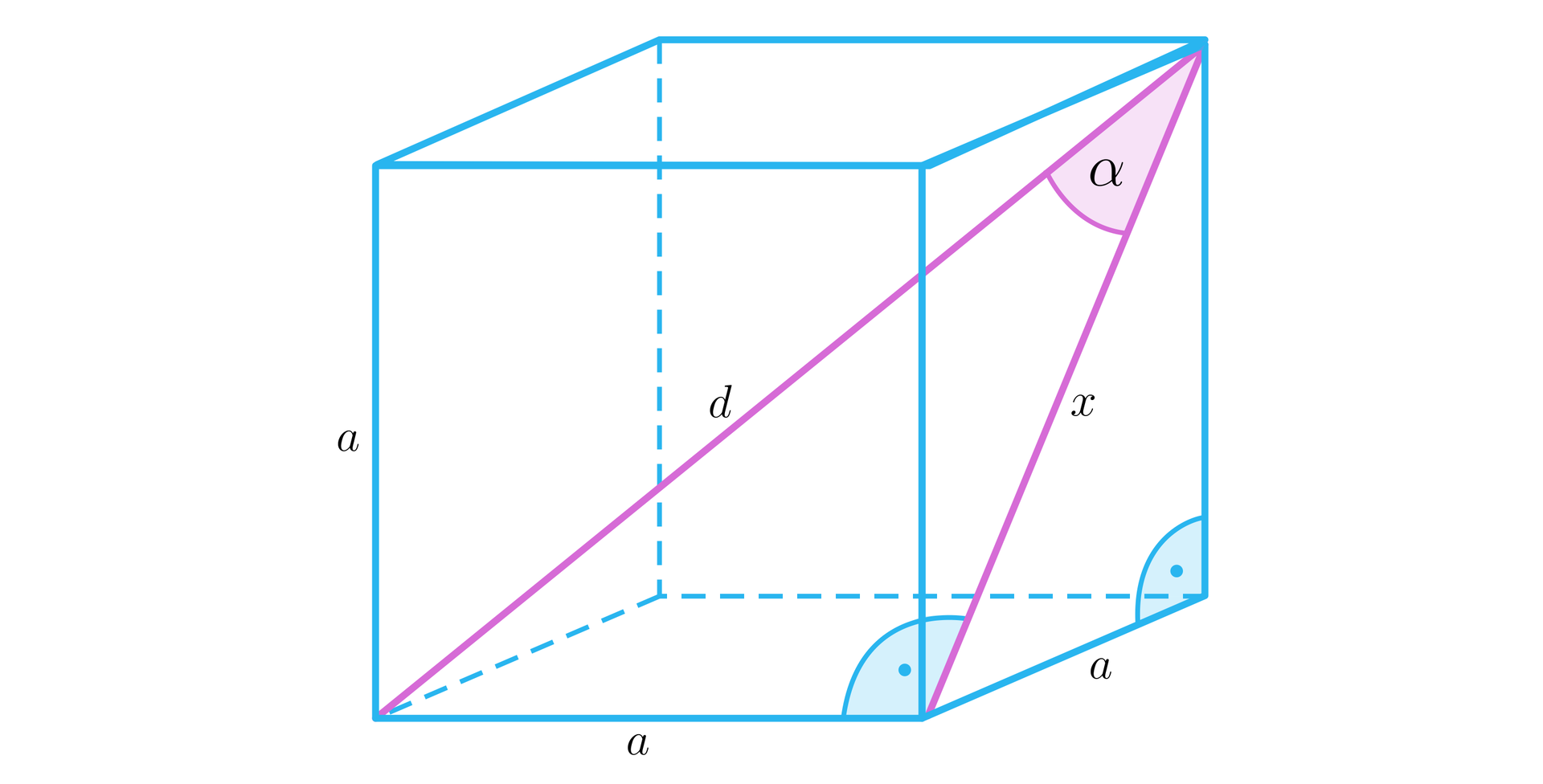
Ilustracja przedstawia sześcian o boku a. Przy jednym z wierzchołków ściany bocznej oznaczono kąt prosty między pionową krawędzią ściany a poziomą krawędzią podstawy bryły. W sześcianie zaznaczono także kąt ostry α, który wyznaczają dwie przekątne: przekątna bryły d oraz przekątna ściany bocznej x. Kąt α znajduje się między nimi.

Długość przekątnej ściany bocznej obliczamy, korzystając z twierdzenia Pitagorasa:

$a^{2} + a^{2} = x^{2}$ .

Wobec tego $x = a \sqrt{2}$ .

Zauważmy, że przekątna sześcianu, przekątna ściany bocznej oraz krawędź podstawy tworzą trójkąt prostokątny, jak na poniższym rysunku.

RLaNs9LTmUhbU

Rysunek przedstawia trójkąt prostokątny o podstawie a, o pionowej przyprostokątnej x oraz o przeciwprostokątnej d. Na ilustracji zaznaczono dwa kąty wewnętrze trójkąta. Między bokami d oraz x znajduje się kąt α i między bokami a oraz x zaznaczono kąt prosty.

Zatem, korzystając z definicji funkcji trygonometrycznej tangens dla kąta $α$ , mamy zależność:

$tg α = \frac{a}{x} = \frac{a}{a \sqrt{2}} = \frac{\sqrt{2}}{2}$ .

Ponieważ $\frac{\sqrt{2}}{2} \approx 0, 707$ , zatem $α = 35 °$ .

Słownik

funkcje trygonometryczne kąta ostrego w trójkącie prostokątnym

funkcje wyrażające stosunki pomiędzy długościami boków trójkąta prostokątnego względem miar jego kątów wewnętrznych

Wprowadzenie

Schemat interaktywny

Słownik