Przeczytaj
Jednym z podstawowych problemów optymalizacji jest znajdowanie najmniejszej lub największej wartości funkcji . Zaczniemy nasze rozważania od klasycznego przykładu inspirowanego rzeczywistym problemem.
Dwumetrowy drut wyginamy tak, by otrzymać prostokątną ramkę. W jaki sposób powinniśmy to zrobić, jeżeli chcemy, aby otrzymany prostokąt miał jak największe pole, a w jaki, jeżeli chcemy, by pole było możliwie najmniejsze?
Jeżeli jeden z boków otrzymanych po wygięciu oznaczymy przez , to otrzymamy sytuację jak na rysunku poniżej.
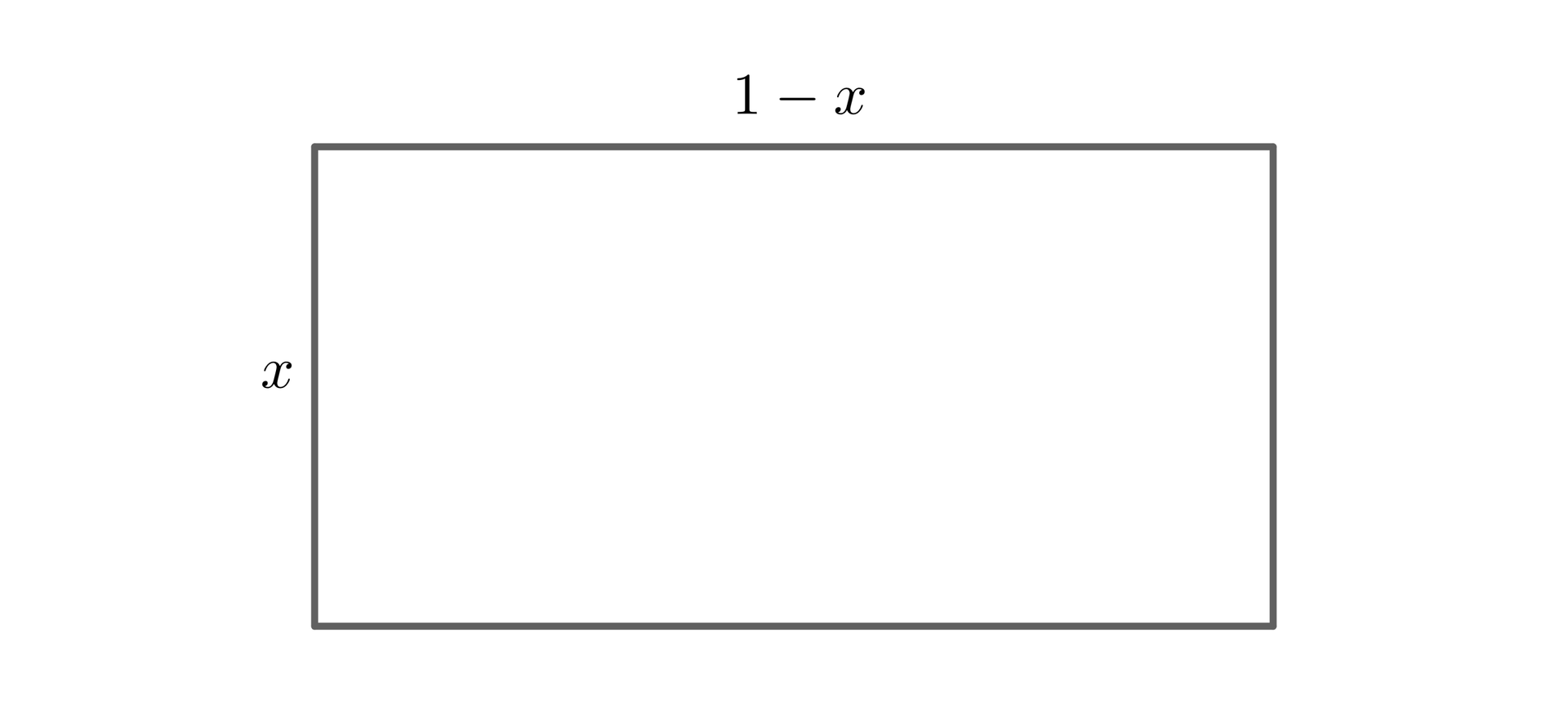
Oczywiście, długości warte rozważania to te z przedziału . Każdej długości przyporządkujmy więc pole prostokąta o boku . Otrzymamy wówczas funkcję , , której wykres ma postać:
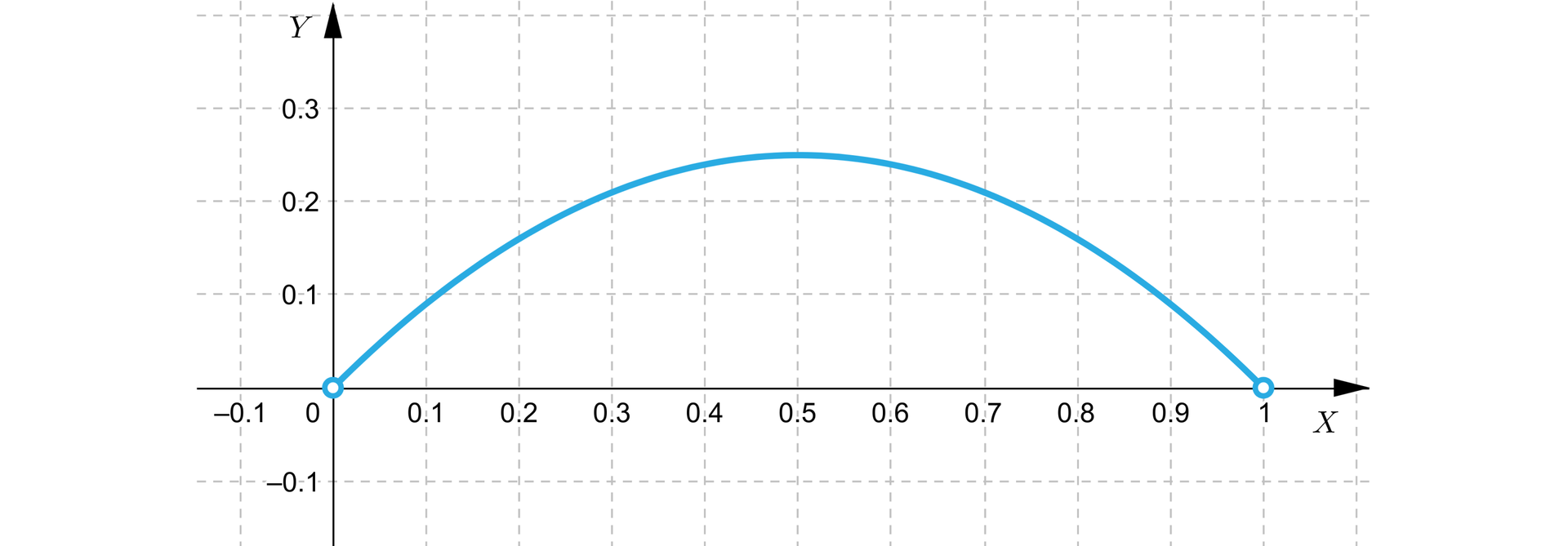
Nietrudno zauważyć, że funkcja osiąga największą wartość dla , wówczas . Zatem, aby zapewnić największe pole rozważanej konstrukcji, należy zbudować kwadrat o boku metra.
jest bokiem zapewniającym największe pole rozważanej konstrukcji. Można to też wyznaczyć algebraicznie licząc odciętą wierzchołka paraboli: .
Nie istnieje jednak długość boku, dla której otrzymany prostokąt miałby możliwie najmniejsze pole. Tym samym drugi z problemów nie posiada rozwiązania.
Powyższy przykład pokazuje, że problem znajdowania najmniejszej lub największej wartości funkcji może nie posiadać rozwiązania. Problemem nie jest jedynie to, że przedział jest otwarty.
Niech funkcja będzie dana wzorem
.
Wówczas wykres funkcji przedstawia się następująco:
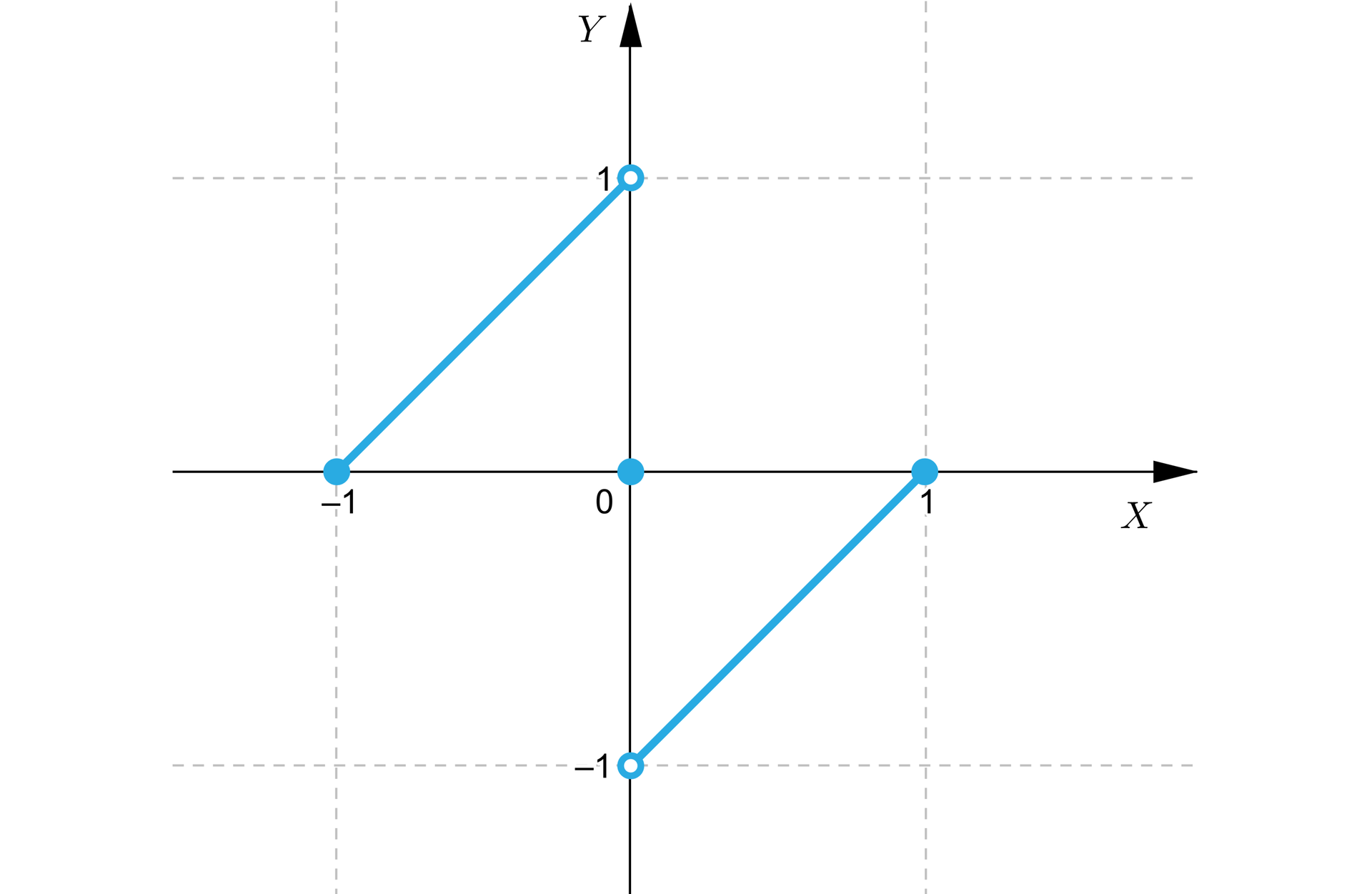
W konsekwencji nie ma tak największej jak i najmniejszej wartości.
Zauważamy więc, że problemem jest także nieciągłość funkcji.
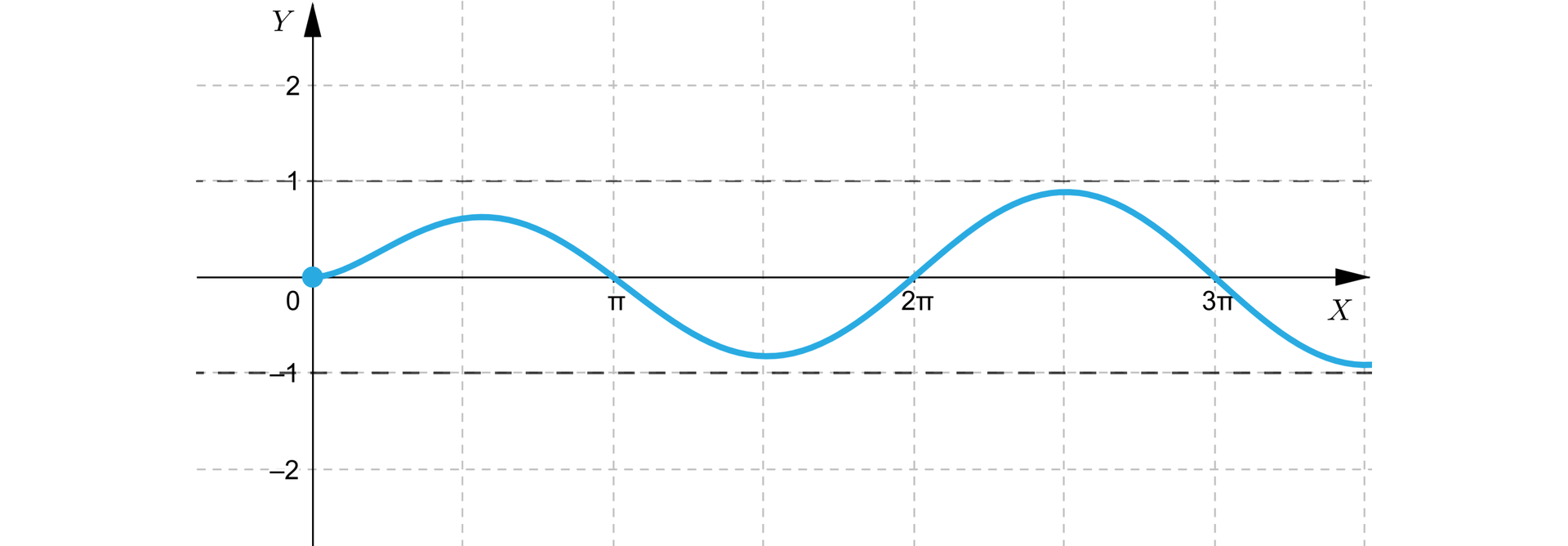
Niech funkcja będzie dana wzorem .
Biorąc ciągi i określone wzorami
oraz
otrzymamy
oraz .
Z drugiej strony, dla każdego mamy
,
a więc wartości i nie mogą być przyjmowane w żadnym punkcie dziedziny. Można to także zauważyć na podstawie wykresu.
Powyższe przykłady mogą stanowić pomoc w zapamiętaniu wszystkich założeń twierdzenia Weierstrassa.
Mówimy, że funkcja osiąga wartość gdy istnieje takie , że .
Każda funkcja ciągłafunkcja ciągła określona na domkniętym i ograniczonym odcinku osiąga wartość najmniejszą i największą.
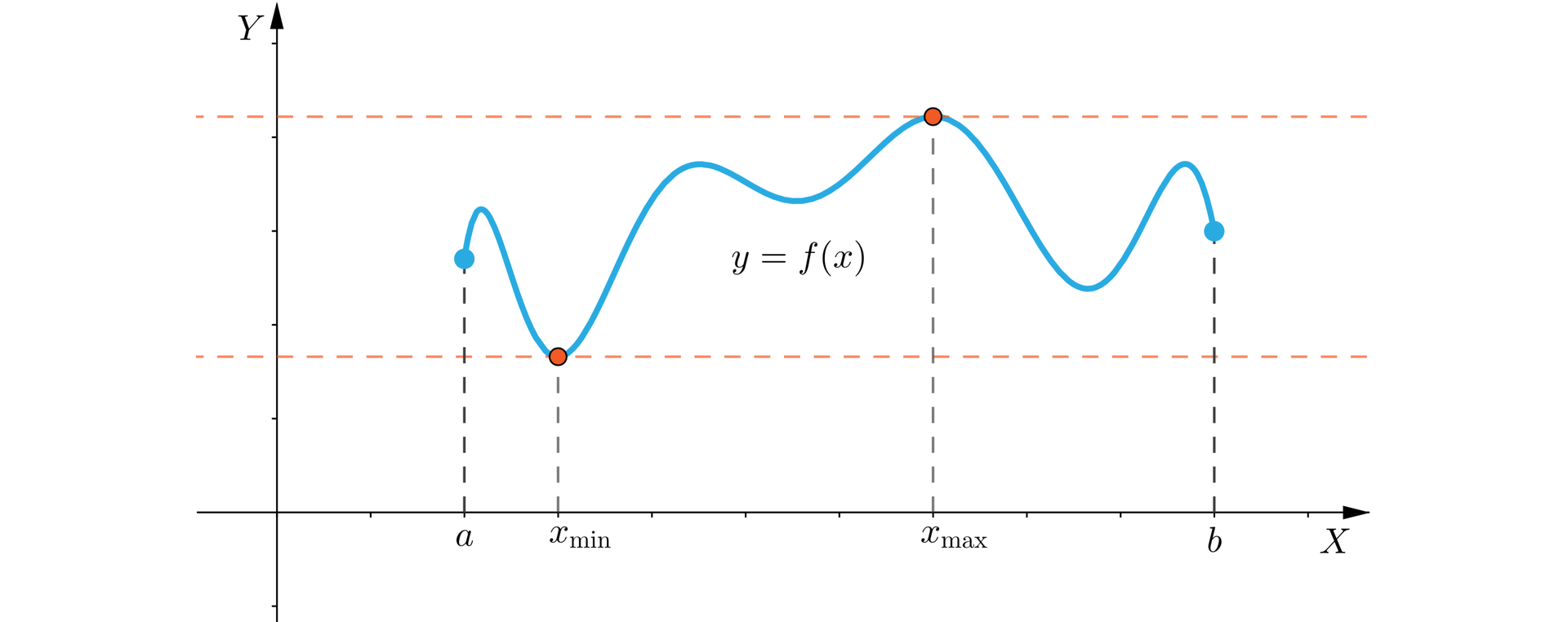
Możemy przeformułować powyższe twierdzenie w następujący sposób.
Niech będzie funkcją ciągłą. Wówczas istnieją takie , że dla każdego zachodzi oraz .
Trzeba podkreślić, że argument minimumargument minimum i argument maksimumargument maksimum gwarantowane przez twierdzenie Weierstrassa nie muszą być wyznaczane jednoznacznie.
Niech funkcja będzie dana wzorem .
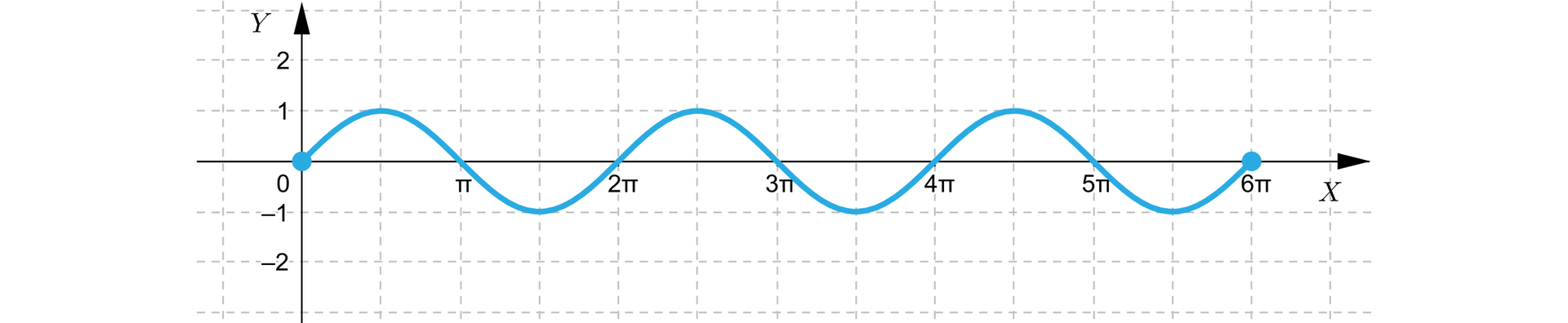
Z wykresu bez trudu otrzymujemy, że argumentami minimum są , i . Z kolei , i są argumentami maksimum funkcji .
Słownik
taki argument funkcji , dla którego funkcja ta osiąga najmniejszą wartość ze zbioru wartości
taki argument funkcji , dla którego funkcja ta osiąga największą wartość ze zbioru wartości
funkcja spełniająca jeden z równoważnych warunków ciągłości (Cauchy'ego lub Heinego)