Przeczytaj

Jednym z najprostszych problemów geometrii, prowadzącym do układu równań liniowych, jest wyznaczanie długości boków wielokąta w sytuacji, gdy znamy jego obwód oraz zależności zachodzące pomiędzy jego bokami. Ponieważ najprostszymi wielokątami są prostokąty, więc pierwszy przykład będzie dotyczył właśnie tej figury geometrycznej.

Pole prostokąta o bokach długości $a$ i $b$ obliczamy ze wzoru

P = a b

a obwód

L = 2 (a + b)

Przykład 1

Oblicz pole prostokątapole prostokątapole prostokąta, którego obwód wynosi $72$ , a jeden z boków jest o $10$ dłuższy od drugiego.

Rozwiązanie

Oznaczmy przez $a$ długość krótszego, a przez $b$ długość dłuższego boku i zapiszmy podane w zadaniu informacje w formie układu równań:

$\{\begin{cases} b = a + 10 \\ 2 (a + b) = 72 | : 2 \end{cases}$

$\{\begin{cases} b - a = 10 \\ a + b = 36 \end{cases}$

Gdy dodamy równania stronami, to otrzymamy $2 b = 46$ , więc $b = 23$ , a stąd $a = 13$ .Teraz możemy już obliczyć pole $P = 13 \cdot 23 = 299$ .

Szczególnym prostokątem jest kwadrat. W dowolnym kwadracie długość przekątnej $d$ zależy od długości jego boku $a$ : $d = a \sqrt{2}$ . Gdy mamy informację o dodatkowej zależności pomiędzy bokiem, a przekątną kwadratu, np. o ile przekątna jest dłuższa od boku, to zapisując i rozwiązując odpowiedni układ równań możemy wyliczyć ich długości.

Przykład 2

Oblicz pole kwadratupole kwadratupole kwadratu, którego przekątna jest o $12$ dłuższa od boku.

Rozwiązanie

Niech $a$ oznacza bok szukanego kwadratu, a $d$ jego przekątną. Wiedząc, że $d$ jest o $12$ dłuższa od $a$ , możemy zapisać układ równań:

$\{\begin{cases} d = a + 12 \\ d = a \sqrt{2} \end{cases}$

$\{\begin{cases} d = a + 12 \\ a \sqrt{2} = a + 12 \end{cases}$

$\{\begin{cases} d = a + 12 \\ a \sqrt{2} - a = 12 \end{cases}$

$\{\begin{cases} d = a + 12 \\ a (\sqrt{2} - 1) = 12 \end{cases}$

$\{\begin{cases} d = a + 12 \\ a = \frac{12}{\sqrt{2} - 1} \end{cases}$

Usuwamy niewymierność z mianownika: $\frac{12 \cdot (\sqrt{2} + 1)}{(\sqrt{2} - 1) (\sqrt{2} + 1)} = \frac{12 \sqrt{2} + 12}{2 - 1} = 12 \sqrt{2} + 12$ i otrzymujemy, że bok kwadratu ma długość $a = 12 \sqrt{2} + 12$ , a jego przekątna $d = 12 \sqrt{2} + 24$ .

Pozostało obliczyć pole:

$P = a^{2} = {(12 \sqrt{2} + 12)}^{2} = 288 + 288 \sqrt{2} + 144 = 432 + 288 \sqrt{2}$ .

Innymi przykładami wykorzystania układów równań w zadaniach geometrycznych, są zadania o kątach w wielokątach, w tym również o kątach trójkąta.

Suma miar wszystkich kątów wewnętrznych trójkąta jest równa $180 °$ . W przypadku trójkąta prostokątnego z tego faktu wynika, że suma miar jego kątów ostrych jest równa $90 °$ .

Przykład 3

Wyznacz miary kątów ostrych trójkąta prostokątnego, w którym miara jednego z kątów ostrych jest o $40 %$ większa od miary drugiego kąta ostrego.

Rozwiązanie

Oznaczmy miarę mniejszego z kątów przez $α$ , a większego przez $β$ . Suma miar kątów ostrych trójkąta prostokątnego jest równa $90 °$ . Ponieważ kąt $β$ jest o $40 %$ większy niż $α$ , więc $β = 140 % \cdot α = 1, 4 α$ .

Zatem:

$\{\begin{cases} α + β = 90 ° \\ β = 1, 4 α \end{cases}$

$\{\begin{cases} α + 1, 4 α = 90 ° \\ β = 1, 4 α \end{cases}$

$\{\begin{cases} 2, 4 α = 90 ° | : 2, 4 \\ β = 1, 4 α \end{cases}$

$\{\begin{cases} α = 37, 5 ° \\ β = 1, 4 α \end{cases}$

$\{\begin{cases} α = 37, 5 ° \\ β = 52, 5 ° \end{cases}$

Odpowiedź:

Kąty ostre tego trójkąta mają miary $37, 5 °$ i $52, 5 °$ .

Jest wiele wzorów na pole trójkątapole trójkątapole trójkąta, ale najpopularniejszym z nich jest $P = \frac{1}{2} a h$ , gdzie $a$ to długość jednego z boków trójkąta, a $h$ – długość wysokości opuszczonej na ten bok. Ponieważ trójkąt ma trzy boki, więc ma również trzy wysokości, a z tego wynika, że

P = \frac{1}{2} a h_{a} = \frac{1}{2} b h_{b} = \frac{1}{2} c h_{c}

gdzie $h_{a}$ , $h_{b}$ i $h_{c}$ to wysokości trójkąta opuszczone odpowiednio na boki długości $a$ , $b$ i $c$ .

Zauważmy, że z powyższego wynika, że w dowolnym trójkącie iloczyny długości boków i odpowiadających im wysokości są równe.

Przykład 4

Suma długości dwóch boków pewnego trójkąta wynosi $87$ , a wysokości opuszczone na te boki są równe odpowiednio $28$ i $30$ . Oblicz pole tego trójkąta.

Rozwiązanie

Oznaczmy boki trójkąta przez $a$ , $b$ i $c$ i załóżmy, że $a + b = 87$ . Przypuśćmy, że $28$ jest wysokością opuszczoną na bok $a$ , a $30$ – wysokością opuszczoną na bok $b$ . Pole rozważanego trójkąta jest równe $\frac{1}{2} a \cdot 28 = 14 a$ . Z drugiej strony, pole możemy obliczyć jako $\frac{1}{2} b \cdot 30 = 15 b$ . W obydwu przypadkach otrzymamy ten sam wynik, a więc $14 a = 15 b$ . Zapiszmy i rozwiążmy odpowiedni układ równań:

$\{\begin{cases} a + b = 87 \\ 14 a = 15 b \end{cases}$

$\{\begin{cases} a + b = 87 | \cdot 14 \\ 14 a - 15 b = 0 | \cdot (- 1) \end{cases}$

$\{\begin{cases} 14 a + 14 b = 1218 \\ - 14 a + 15 b = 0 \end{cases}$

Po dodaniu do siebie równań otrzymujemy: $29 b = 1218$ , więc $b = 42$ , a $a = 87 - 42 = 45$ . Pole trójkąta jest równe $P = 14 a = 14 \cdot 45 = 630$ .

Odpowiedź:

Pole trójkąta jest równe $630$ .

Kąt środkowy

Definicja: Kąt środkowy

Kątem środkowym nazywamy kąt, którego wierzchołek leży w środku okręgu, a ramiona są półprostymi zawierającymi promienie tego okręgu.

Kąt wpisany

Definicja: Kąt wpisany

Kątem wpisanym nazywamy kąt, którego wierzchołek jest dowolnym punktem okręgu, a ramiona są półprostymi zawierającymi cięciwy okręgu.

Jeśli w danym okręgu ramiona kąta środkowego i wpisanego przecinają się, to wyznaczają łuk, na którym są oparte.

o kącie środkowym

Twierdzenie: o kącie środkowym

Kąt środkowy ma miarę dwukrotnie większą od miary kąta wpisanego opartego na tym samym łuku.

R1GqiF7okmcYd

Ilustracja przedstawia okrąg z zaznaczonymi kątami. Kąt wpisany ma swój wierzchołek w punkcie C, punkt znajduje się na okręgu. Ramiona kąta wpisanego to AC oraz BC. Kąt między ramionami ma miarę alfa. Kąt środkowy ma swój wierzchołek w punkcie S który jest środkiem okręgu. Ramiona okręgu to odcinki A S oraz B S. Kąt między ramionami ma miarę dwa alfa.

Przykład 5

Suma miar kątów środkowego i wpisanego opartych na tym samym łuku okręgu jest równa $219 °$ . Wyznacz miary tych kątów.

Rozwiązanie

Oznaczmy przez $α$ miarę kąta wpisanego, a przez $β$ miarę kąta środkowego i korzystając z faktu, że $β = 2 α$ rozwiążmy zadanie:

$\{\begin{cases} β = 2 α \\ α + β = 219 ° \end{cases}$

$\{\begin{cases} β = 2 α \\ α + 2 α = 219 ° \end{cases}$

$\{\begin{cases} β = 2 α \\ 3 α = 219 ° | : 3 \end{cases}$

$\{\begin{cases} β = 146 ° \\ α = 73 ° \end{cases}$

Odpowiedź:

Kąt wpisanykąt wpisanyKąt wpisany ma miarę $73 °$ , a kąt środkowykąt środkowykąt środkowy $146 °$ .

Gdy wiemy, jak zmienia się pole prostokąta, jeśli wydłużymy bądź skrócimy jego boki na dwa sposoby, to rozwiązując odpowiedni układ równań, możemy obliczyć jego boki.

Przykład 6

Jeśli krótsze boki pewnego prostokąta wydłużymy o $6$ , a dłuższe skrócimy o $6$ , to otrzymamy prostokąt o polu o $48$ większym od pola początkowego prostokąta. Jeśli natomiast wszystkie boki tego prostokąta wydłużymy o $4$ , to otrzymamy prostokąt o polu o $104$ większym od pola początkowego prostokąta. Znajdź długości boków tego prostokąta.

Rozwiązanie

Oznaczmy przez $a$ długość krótszego boku, a przez $b$ długość dłuższego boku początkowego prostokąta. Jego pole jest równe $a b$ . Jeśli wydłużymy krótsze boki o $6$ , a dłuższe skrócimy o $6$ , to pole nowego prostokąta będzie wynosić:

$(a + 6) (b - 6)$ .

Jeśli natomiast wszystkie boki wydłużymy o $4$ , to otrzymamy prostokąt o polu

$(a + 4) (b + 4)$ .

Zapiszmy układ równań:

$\{\begin{cases} (a + 6) (b - 6) = a b + 48 \\ (a + 4) (b + 4) = a b + 104 \end{cases}$

$\{\begin{cases} a b - 6 a + 6 b - 36 = a b + 48 | - a b + 36 \\ a b + 4 a + 4 b + 16 = a b + 104 | - a b - 16 \end{cases}$

$\{\begin{cases} - 6 a + 6 b = 84 | : 6 \\ 4 a + 4 b = 88 | : 4 \end{cases}$

$\{\begin{cases} - a + b = 14 \\ a + b = 22 \end{cases}$

Gdy dodamy do siebie równania stronami, to otrzymamy $2 b = 36$ , a stąd $b = 18$ i $a = 22 - 18 = 4$ .

Odpowiedź:

Boki tego prostokąta mają długości $4$ i $18$ .

Rozważmy trapez $A B C D$ , który nie jest równoległobokiem, o podstawach $A B$ i $C D$ . Przedłużamy ramiona trapezu aż do punktu przecięcia $S$ .

RMLNc5U1vkdMM

Ilustracja przedstawia trójkąt A B S. Kąt przy wierzchołku A ma miarę alfa, a przy wierzchołku B ma miarę beta. W środku trójkąta znajduję się drugi trójkąt C D S. Kąt przy wierzchołku D ma miarę alfa, przy wierzchołku C ma miarę beta, a przy wierzchołku S ma miarę gamma. Odcinek AB jest równoległy do odcinka CD.

Ponieważ $A B$ i $C D$ są równoległe, więc kąty $∢ B A D$ i $∢ C D S$ są kątami odpowiadającymi i mają równe miary. Analogicznie, kąty $∢ A B C$ i $∢ D C S$ mają równe miary. Z zasady kąt–kąt–kąt podobieństwa trójkątów wynika, że trójkąty $A B S$ i $D C S$ są podobne. Dlatego:

\frac{|D S|}{|D C|} = \frac{|A S|}{|A B|}

\frac{|C S|}{|D C|} = \frac{|B S|}{|A B|}

Przykład 7

Przedłużamy ramiona trapezu $A B C D$ o podstawach $A B$ i $C D$ aż do punktu przecięcia $S$ (zobacz rysunek powyżej). Wiedząc, że odcinek $D S$ ma długość $6$ , ramię $A D$ – $12$ , wysokość – $7$ , a polepole trapezupole trapezu wynosi $35$ , oblicz długości podstaw tego trapezu.

Rozwiązanie

Oznaczmy przez $a$ długość podstawy $A B$ , a przez $b$ długość podstawy $C D$ .

Ponieważ $\frac{|D S|}{|D C|} = \frac{|A S|}{|A B|}$ , więc

$\frac{6}{b} = \frac{18}{a}$ , a stąd $6 a = 18 b$ .

Zapiszmy układ równań:

$\{\begin{cases} 6 a = 18 b | : 6 \\ \frac{(a + b) \cdot 7}{2} = 35 | \cdot \frac{2}{7} \end{cases}$

$\{\begin{cases} a = 3 b \\ a + b = 10 \end{cases}$

$\{\begin{cases} a = 3 b \\ 3 b + b = 10 \end{cases}$

$\{\begin{cases} a = 3 b \\ 4 b = 10 | : 4 \end{cases}$

$\{\begin{cases} a = 7, 5 \\ b = 2, 5 \end{cases}$

Odpowiedź:

Podstawa $A B$ ma długość $7, 5$ , a $C D$ – długość $2, 5$ .

W niektórych zadaniach z geometrii niewiadomymi mogą być pola figur płaskich. Zapoznajmy się z przykładem.

Przykład 8

W trójkącie $A B C$ na boku $B C$ zaznaczono taki punkt $D$ , że stosunek długości odcinka $C D$ do $D B$ jest równy $2 : 3$ . Na boku $A B$ zaznaczono natomiast punkt $E$ tak, że stosunek długości odcinków $A E$ i $E B$ wynosi $4 : 1$ , odpowiednio. Punkt $S$ jest punktem przecięcia odcinków $A D$ i $C E$ . Oblicz pola trójkątów $E B S$ i $D B S$ wiedząc, że pole trójkątapole trójkątapole trójkąta $A B C$ wynosi $110$ .

Rozwiązanie

Rl20oo8hRShBA

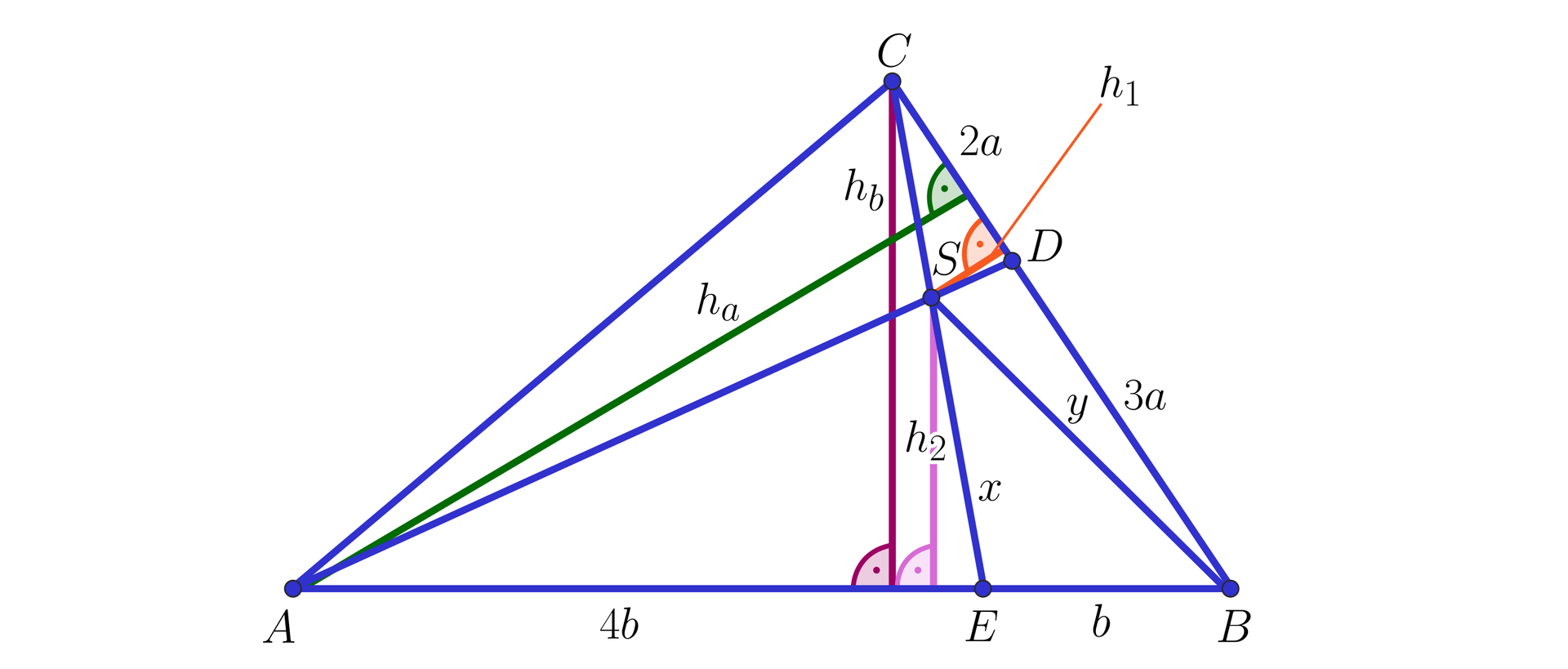
Ilustracja przedstawia trójkąt A B C. Z wierzchołka A wychodzi prosta mająca swój koniec na boku B C. Tworzy się punkt D dzielący ramię w stosunku dwa do trzech. Dlatego odcinek B D ma długość 3a, a odcinek CD ma długość 2a. Z wierzchołka C wychodzi prosta mająca swój koniec na boku A B. Tworzy się punkt E dzielący podstawę A B w stosunku cztery do jednego. Dlatego odcinek A E ma długość 4b, a odcinek B E ma długość b Z wierzchołka B wychodzi prosta mająca swój koniec w punkcie przecięcia pozostałych prostych. Tworzy się punkt S. Odcinek B S ma długość y. Odcinek E S ma długość x. Z wierzchołka C na podstawę upuszczono wysokość h indeks dolny b koniec indeksu. Z wierzchołka A upuszczono na odcinek B C wysokość h indeks dolny a koniec indeksu. W trójkącie C D S upuszczono wysokość h indeks dolny jeden koniec indeksu na odcinek CD. Z punktu S do podstawy trójkąta upuszczono wysokość h indeks dolny dwa koniec indeksu.

Ponieważ $|C D| : |D B| = 2 : 3$ , więc istnieje liczba dodatnia $a$ taka, że $|C D| = 2 a$ i $|D B| = 3 a$ . Podobnie, ponieważ $|A E| : |E B| = 4 : 1$ , więc istnieje liczba dodatnia $b$ taka, że $|A E| = 4 b$ i $|E B| = b$ .

Zauważmy, że wysokość $h_{1}$ trójkąta $B C S$ opadająca na bok $B C$ jest jednocześnie wysokością trójkąta $D B S$ (opadającą na bok $D B$ ) oraz wysokością trójkąta $D C S$ (opadającą na bok $C D$ ). Wyznaczmy pola tych trójkątów:

$P_{B C S} = \frac{5 a h_{1}}{2}$ , $P_{D B S} = \frac{3 a h_{1}}{2}$ , $P_{D C S} = \frac{2 a h_{1}}{2}$ .

Oznaczmy pole trójkąta $P_{D B S}$ przez $y$ i zauważmy, że $P_{D C S} = \frac{2}{3} y$ .

Zauważmy, że wysokość $h_{2}$ trójkąta $A B S$ opadająca na bok $A B$ jest jednocześnie wysokością trójkąta $E B S$ (opadającą na przedłużenie boku $E B$ ) oraz wysokością trójkąta $E A S$ (opadającą na bok $A E$ ). Wyznaczmy pola tych trójkątów:

$P_{A B S} = \frac{5 b h_{2}}{2}$ , $P_{E B S} = \frac{b h_{2}}{2}$ , $P_{E A S} = \frac{4 b h_{2}}{2}$ .

Oznaczmy pole trójkąta $P_{E B S}$ przez $x$ i zauważmy, że $P_{E A S} = 4 x$ .

Ponieważ wysokość $h_{a}$ trójkąta $A B C$ opadająca na bok $B C$ jest jednocześnie wysokością trójkąta $A B D$ opadającą na bok $B D$ i bok $|B D| = \frac{3}{5} |B C|$ , więc

$P_{B A D} = \frac{3}{5} P_{A B C} = \frac{3}{5} \cdot 110 = 66$ .

Z drugiej strony,

$P_{B A D} = P_{E A S} + P_{E B S} + P_{D B S} = 4 x + x + y = 5 x + y$ .

Podobnie, ponieważ wysokość $h_{b}$ trójkąta $A B C$ opadająca na bok $A B$ jest jednocześnie wysokością trójkąta $B C E$ opadającą na bok $B E$ i bok $|B E| = \frac{1}{5} |A B|$ , więc

$P_{B C E} = \frac{1}{5} P_{A B C} = \frac{1}{5} \cdot 110 = 22$

Z drugiej strony,

$P_{B C E} = P_{E B S} + P_{D B S} + P_{D C S} = x + y + \frac{2}{3} y = x + \frac{5}{3} y$

Zapiszmy układ równań:

$\{\begin{cases} 5 x + y = 66 | \cdot 5 \\ x + \frac{5}{3} y = 22 | \cdot (- 3) \end{cases}$

$\{\begin{cases} 25 x + 5 y = 330 \\ - 3 x - 5 y = - 66 \end{cases}$

Gdy dodamy do siebie równania stronami, to otrzymamy: $22 x = 264$ , a stąd $x = 12$ i $y = 66 - 5 \cdot 12 = 6$ .

Odpowiedź:

Pole trójkąta $E B S$ wynosi $12$ , a pole trójkąta $D B S$ jest równe $6$ .

Słownik

pole trójkąta

pole trójkąta o bokach $a$ , $b$ , $c$ i wysokościach odpowiednio $h_{a}$ , $h_{b}$ , $h_{c}$ odpowiadającym tym bokom można obliczyć ze wzorów:

P = \frac{1}{2} a h_{a}

lub

P = \frac{1}{2} b h_{b}

lub

P = \frac{1}{2} c h_{c}

z tego wynika, że

\frac{1}{2} a h_{a} = \frac{1}{2} b h_{b} = \frac{1}{2} c h_{c}

suma miar wewnętrznych trójkąta jest równa $180 °$ ;

w trójkącie prostokątnym o kątach ostrych $30 °$ i $60 °$ oraz przyprostokątnej leżącej naprzeciw kąta $30 °$ długości $a$ , druga przyprostokątna ma długość $a \sqrt{3}$ , a przeciwprostokątna ma długość $2 a$

pole prostokąta

pole prostokąta o bokach $a$ i $b$ wyznaczamy ze wzoru

P = a b

a obwód ze wzoru

L = 2 (a + b)

pole kwadratu

pole kwadratu o boku $a$ wyznaczamy ze wzoru

P = a^{2}

obwód

L = 4 a

a jego przekątna jest równa

d = a \sqrt{2}

pole trapezu

pole trapezu o podstawach $a$ i $b$ oraz wysokości $h$ jest równe

\frac{(a + b) h}{2}

odcinek łączący środki ramion trapezu ma długość

\frac{a + b}{2}

w trapezie równoramiennym wysokość poprowadzona z wierzchołka górnej podstawy dzieli dolną postawę na dwa odcinki długości odpowiednio $\frac{a - b}{2}$ i $\frac{a + b}{2}$

kąt środkowy

kąt, którego wierzchołek leży w środku okręgu, a ramiona są półprostymi zawierającymi promienie tego okręgu

kąt wpisany

kąt, którego wierzchołek jest dowolnym punktem okręgu, a ramiona są półprostymi zawierającymi cięciwy okręgu;

miara kąta środkowego w danym okręgu jest dwa razy większa od miary kąta wpisanego opartego na tym samym łuku

Wprowadzenie

Prezentacja multimedialna

Słownik