Wyznaczymy wartość parametru $m$ we wzorze funkcji $f\left(x\right)=\frac{-4x-2m}{x-4}$ wiedząc, że miejscem zerowym funkcji jest liczba $\left(-3\right)$.

Rozwiązanie

Liczba $\left(-3\right)$ jest miejscem zerowym funkcji, jeśli $f\left(-3\right)=0$.

Zatem:

$0=\frac{-4·\left(-3\right)-2m}{-3-4}$

$m=6$

Wyznaczymy wartości parametrów $b$ i $d$ we wzorze funkcji homograficznej $f\left(x\right)=\frac{x+b}{x+d}$ wiedząc, że miejscem zerowym funkcji jest liczba $\left(-4\right)$ oraz funkcja jest malejąca w każdym z przedziałów: $\left(-\infty ;2\right)$; $\left(2;\infty \right)$.

Rozwiązanie

Liczba $\left(-4\right)$ jest miejscem zerowym funkcji, jeśli $f\left(-4\right)=0$.

Zatem:

$0=\frac{-4+b}{-4+d}$

Ze względu na mianownik musimy założyć, że $d\ne 4$.

Patrząc na licznik otrzymujemy, że $b=4$.

Aby wyznaczyć parametr $d$ należy wykorzystać informację dotyczącą monotoniczności. Funkcja jest malejąca w każdym z przedziałów $\left(-\infty ;2\right)$; $\left(2;\infty \right)$, czyli funkcja nie jest określona dla $x=2$. Oznacza to, że $x=2$ jest miejscem zerowym mianownika ułamka opisującego funkcję $f\left(x\right)$.

$0=2+d$

$d=-2$

Odpowiedź:

$b=4$; $d=-2$

Wyznaczymy współczynniki $a$, $b$ oraz $d$ funkcji homograficznej $f\left(x\right)=\frac{ax+b}{x+d}$ na podstawie jej wykresu:

RNkplYxPGB5Fu

Na ilustracji przedstawiono układ współrzędnych z poziomą osią $X$ od minus trzech do sześciu oraz z pionową osią $Y$ od minus trzech do sześciu. Na płaszczyźnie narysowano wykres funkcji, który stanowi hiperbola. Wykres funkcji przebiega przez punkty o współrzędnych $\left(-2;1\right)$, $\left(0;-1\right)$ oraz $\left(4;3\right)$ i $\left(2;5\right)$ oznaczony jako punkt A. Asymptotę poziomą opisuje równanie $y=2$, natomiast pionową $x=1$.

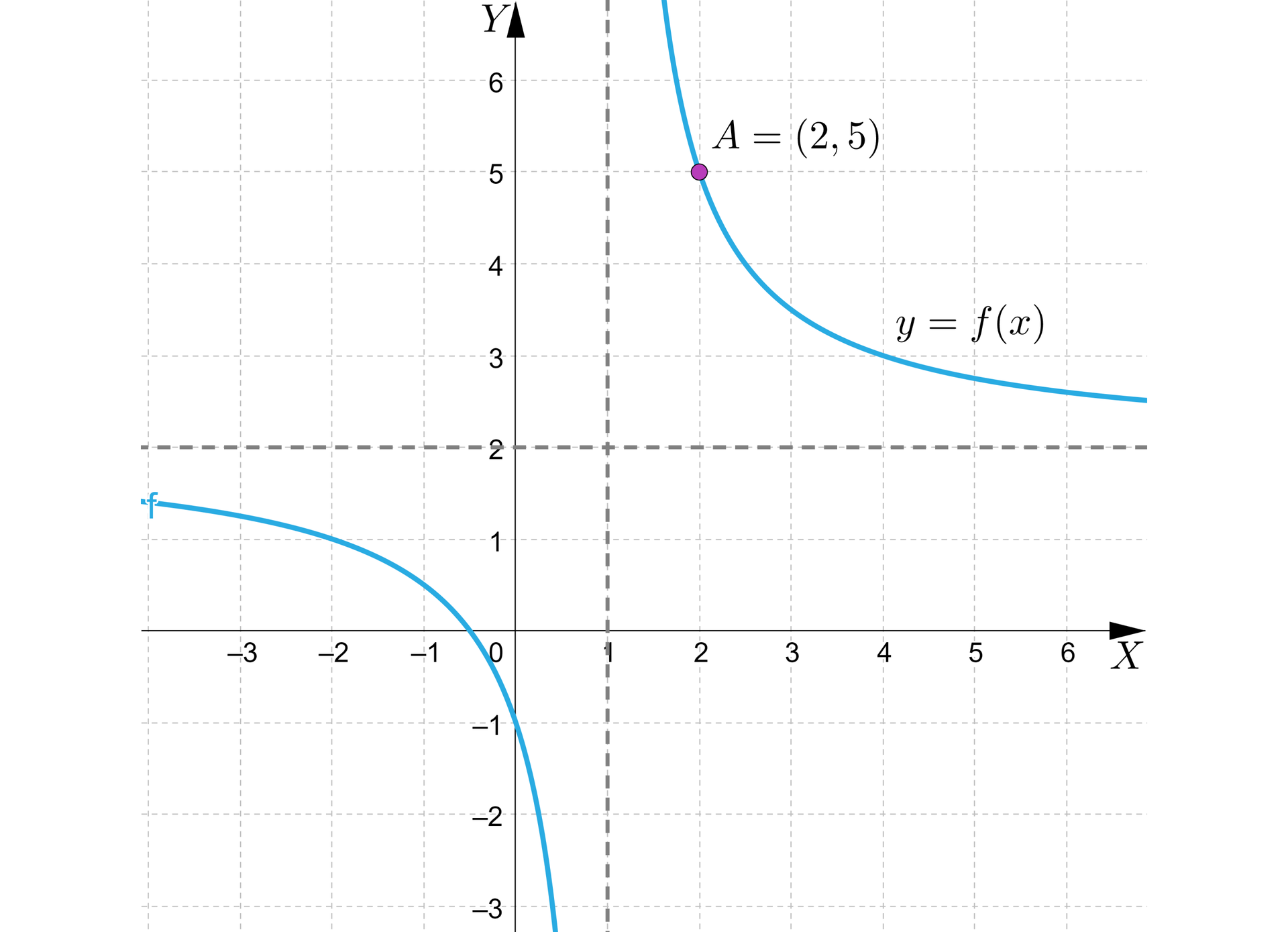
Rozwiązanie

Najpierw przekształcimy wzór funkcji do postaci kanonicznej:

$f\left(x\right)=\frac{ax+b}{x+d}=\frac{a\left(x+d\right)+b-ad}{x+d}=a+\frac{b-ad}{x+d}$

Wynika z tego, że wykres funkcji $f\left(x\right)=\frac{ax+b}{x+d}$ powstał w wyniku przesunięcia równoległego wykresu funkcji $g\left(x\right)=\frac{b-ad}{x}$ o wektor $\overrightarrow{v}=\left[-d;a\right]$.

Z wykresu odczytujemy wektor przesunięcia $\overrightarrow{v}=\left[1;2\right]$

czyli $d=-1$, $a=2$

Wzór funkcji ma postać $f\left(x\right)=\frac{2x+b}{x-1}$ dla  $x\ne 1$.

Następnie z rysunku odczytujemy punkt należący do wykresu funkcji: $A=\left(2;5\right)$. Podstawiamy wspórzędne punktu do wzoru funkcji:

$5=\frac{2·2+b}{2-1}$

zatem $b=1$

Odpowiedź:

$a=2$, $b=1$, $d=-1$

Wyznaczymy współczynniki $a$, $b$ oraz $d$ funkcji homograficznej $f\left(x\right)=\frac{ax+b}{x+d}$ wiedząc, że asymptotamiasymptotaasymptotami wykresu są proste o równaniach: $y=-3$, $x=-2$ oraz wykres funkcji przechodzi przez punkt $A=\left(0;2\right)$.

Rozwiązanie

Najpierw przekształcimy wzór funkcji do postaci kanonicznej:

$f\left(x\right)=\frac{ax+b}{x+d}=\frac{a\left(x+d\right)+b-ad}{x+d}=a+\frac{b-ad}{x+d}$

Wynika z tego, że wykres funkcji $f\left(x\right)=\frac{ax+b}{x+d}$ powstał w wyniku przesunięcia równoległego wykresu funkcji $g\left(x\right)=\frac{b-ad}{x}$ o wektor $\overrightarrow{v}=\left[-d;a\right]$.

Na podstawie równań asymptot wyznaczamy wektor przesunięcia $\overrightarrow{v}=\left[-2;-3\right]$

czyli $d=2$, $a=-3$

Wzór funkcji ma postać: $f\left(x\right)=\frac{-3x+b}{x+2}$dla  $x\ne -2$.

Następnie podstawiamy wspólrzędne punktu $A=\left(0;2\right)$ do wzoru funkcji:

$2=\frac{-3·0+b}{0+2}$

zatem $b=4$

Odpowiedź:

$a=-3$, $b=4$, $d=2$

Wyznaczymy współczynniki $a$ oraz $d$ funkcji homograficznej $f\left(x\right)=\frac{ax+7}{x+d}$ wiedząc, że środkiem symetriiśrodek symetrii figuryśrodkiem symetrii wykresu funkcji jest punkt $S=\left(-4;2\right)$.

Rozwiązanie

Najpierw przekształcimy wzór funkcji do postaci kanonicznej:

$f\left(x\right)=\frac{ax+7}{x+d}=\frac{a\left(x+d\right)+7-ad}{x+d}=a+\frac{7-ad}{x+d}$

Wynika z tego, że wykres funkcji $f\left(x\right)=\frac{ax+7}{x+d}$ powstał w wyniku przesunięcia równoległego wykresu funkcji $f\left(x\right)=\frac{7-ad}{x}$ o wektor $\overrightarrow{v}=\left[-d;a\right]$.

Jeśli środkiem symetrii wykresu funkcji jest punkt $S=\left(-4;2\right)$, to w tym punkcie przecinają się asymptoty wykresu funkcji.

Zatem równania asymptot to: $x=-4$, $y=2$.

Na podstawie rówanań asymptot wyznaczamy wektor przesunięcia $\overrightarrow{v}=\left[-4;2\right]$

czyli $d=4$, $a=2$.

Rozwiążemy graficznie równanie $\frac{2}{x}=-x+3$, gdzie $x\ne 0$.

Rozwiązanie

Narysujemy wykresy funkcji $f\left(x\right)=\frac{2}{x}$ i $g\left(x\right)=-x+3$ i odczytamy  punkty przecięcia tych wykresów.

RsHtKtiiK8lAN

Na ilustracji przedstawiono układ współrzędnych z poziomą osią $X$ od minus pięciu do pięciu oraz z pionową osią $Y$ od minus trzech do pięciu. Na płaszczyźnie narysowano hiperbolę, której gałęzie znajdują się w pierwszej i trzeciej ćwiartce układu współrzędnych. Wykres funkcji przebiega przez punkty o współrzędnych $\left(-2;1\right)$, $\left(-1;-2\right)$ oraz $\left(1;2\right)$ i $\left(2;1\right)$. Narysowano prostą ukośną, przecinającą wykres funkcji w punktach $\left(1;2\right)$ oraz $\left(2;1\right)$.

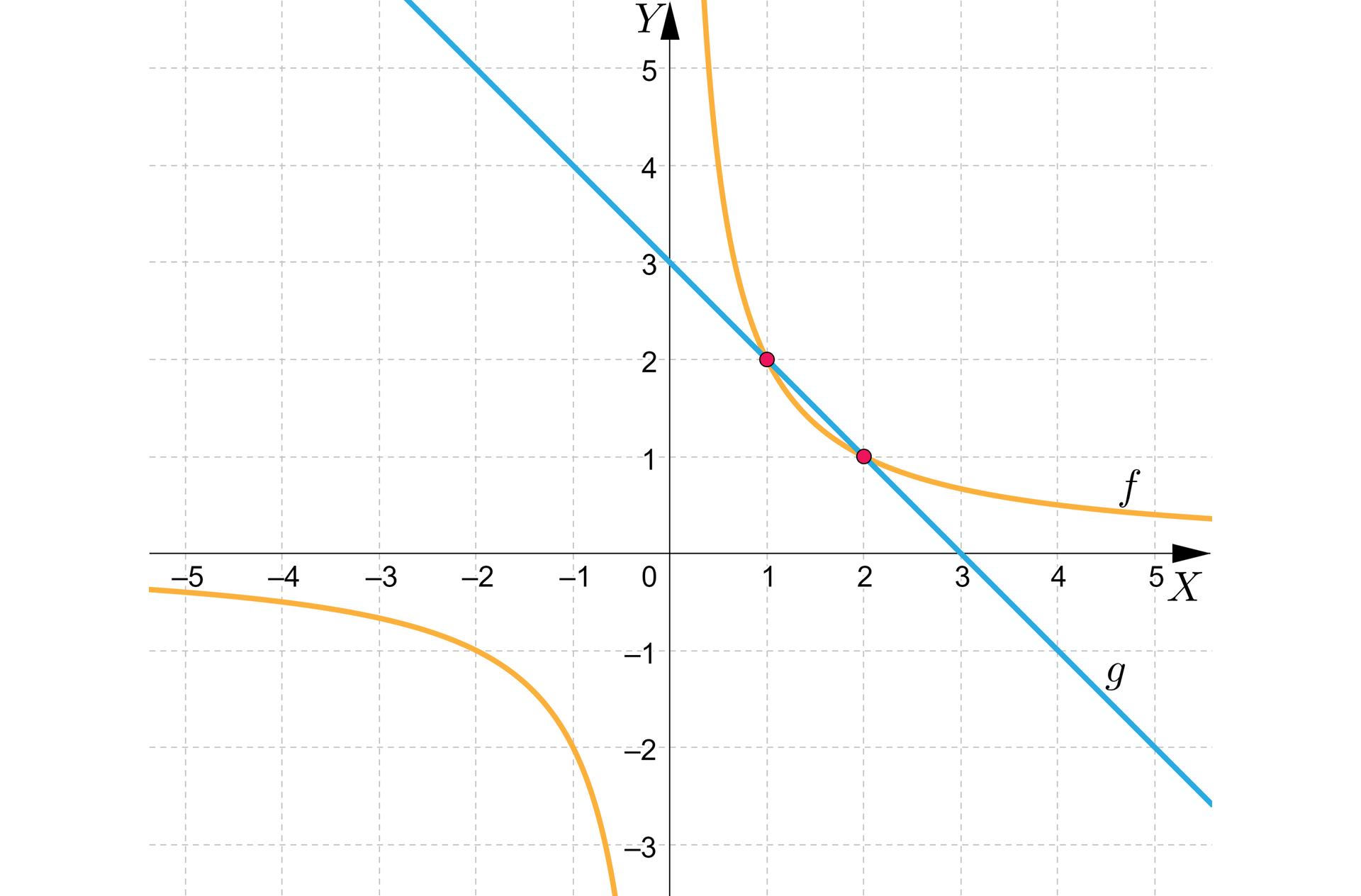
Rozwiązaniem równania są liczby $x=1$ i $x=2$.

Sprawdzimy, który z punktów $A\left(1,3\right)$, $B\left(-5,0\right)$ i $C\left(-1,-1\right)$ należy do wykresu funkcji $f\left(x\right)=\frac{3x-1}{x+5}$

Rozwiązanie

A) Ponieważ $f\left(1\right)=\frac{3-1}{1+5}=\frac{1}{3}\ne 3$, więc punkt $A$ nie należy do wykresu funkcji $f$.

B) Punkt $B$ nie należy do wykresu funkcji $f$, gdyż $x=-5$ nie należy do dziedziny funkcji $f$.

C) Ponieważ $f\left(-1\right)=\frac{-3-1}{-1+5}=-1$, więc punkt $C$ należy do wykresu funkcji $f$.

Rozwiążemy graficznie nierówność $\frac{2x+1}{x+3}\ge x-1$, gdzie $x\ne -3$.

Rozwiązanie

Narysujemy wykresy funkcji $f\left(x\right)=\frac{2x+1}{x+3}$ i $g\left(x\right)=x-1$ i odczytamy zbiór rozwiązań.

Aby narysować wykres funkcji $f$ przekształcimy wzór funkcji z postaci ogólnej do postaci kanonicznej:

$f\left(x\right)=\frac{2x+1}{x+3}=\frac{2x+6-5}{x+3}=\frac{-5}{x+3}+2$

R1AsnYDJYSewM

Na ilustracji przedstawiono układ współrzędnych z poziomą osią $X$ od minus siedmiu do trzech oraz z pionową osią $Y$ od minus trzech do sześciu. Na płaszczyźnie narysowano wykresy dwóch funkcji $f\left(x\right)$ oraz $g\left(x\right)$. Żółtym kolorem narysowano wykres funkcji $f\left(x\right)$, który stanowi hiperbola. Liniami przerywanymi zaznaczono asymptoty wykresu funkcji. Asymptotę pionową opisuje równanie $x=-3$, natomiast poziomą $y=2$. Kolorem czerwonym narysowano wykres funkcji $g\left(x\right)$, który stanowi prosta ukośna, przecinająca jedną z gałęzi hiperboli w punktach o współrzędnych $\left(-2;-3\right)$ oraz $\left(2;1\right)$. Część wykresu funkcji $f\left(x\right)$, która została odcięta przez wykres $g\left(x\right)$ oznaczono kolorem niebieskim.

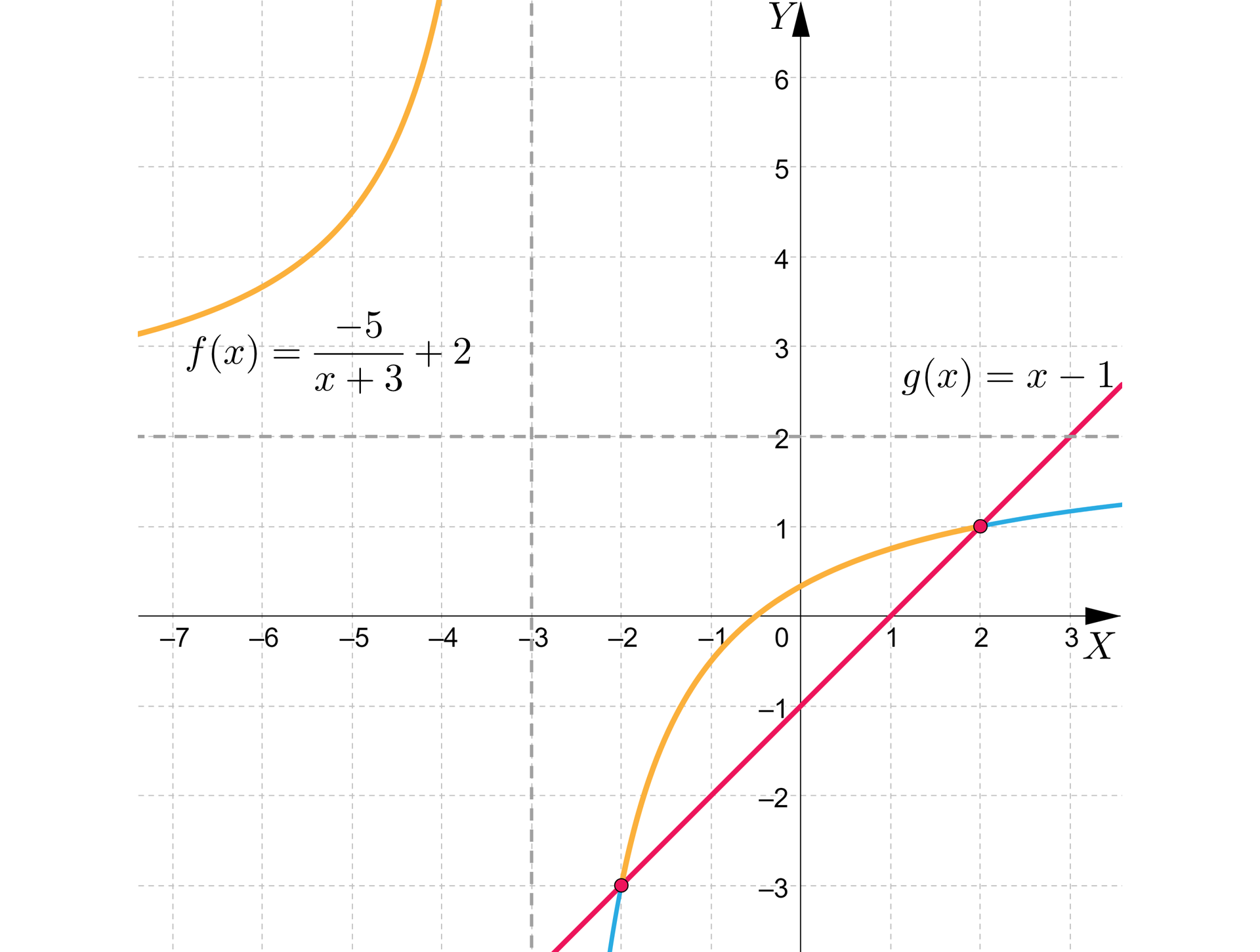
Rozwiązaniem nierówności jest zbiór $\left(-\infty ,-3\right)\cup ⟨-2,2⟩$

prosta jest asymptotą danej krzywej, jeśli dla punktu oddalającego się nieograniczenie wzdłuż krzywej odległość tego punktu od prostej dąży do zera; asymptota funkcji to asymptota krzywej stanowiącej wykres funkcji

funkcja, która jest ilorazem dwóch wielomianów

jest to punkt względem którego figura jest do siebie środkowosymetryczna; figura taka, gdy zostanie obrócona o 180 stopni wokół swojego środka symetrii, nałoży się na siebie